第四章四边形性质探索复习题
1、如图2，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是_______.
2、如图，矩形ABCD中，AB＝3，BC＝4，如果将该矩形沿对角线BD折叠，那么图中阴影部分的面积是
.
3、如图，在等腰梯形ABCD中，AD∥BC，AB=CD，且AC⊥BD，AF是梯形的高，梯形面积是49cm2，则AF= ；
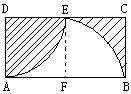
4、已知：如图，矩形ABCD的长和宽分别为2和1，以D为圆心，AD为半径作AE弧，再以AB的中点F为圆心，FB长为半径作BE弧，则阴影部分的面积为
；
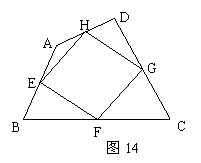
5、如图14，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，请添加一个条件，使四边形EFGH为菱形，并说明理由．
解：添加的条件：
理由：
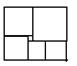
6、如图，一个长方形被划分成大小不等的6个正方形，已知中间的最小的正方形的面积为1平方厘米，则这个长方形的面积为 ；
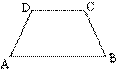7、如图,请写出等腰梯形
∥
特有而一般梯形不具有的三个特征:__________ ______;
________ _________;
__________ ________.
8、如图,已知在等腰梯形ABCD中,AD∥BC.
(1) 若AD＝5, BC＝11,梯形的高是4,求梯形的周长.
(2) 若AD＝a, BC＝b, 梯形的高是h,梯形的周长为c.
则c＝ . (请用含a、b、h的代数式表示; 答案直接写在横线上,不要求证明.)
9、已知：在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD,AD=3cm,BC=7cm,则梯形的高是_______cm.
10、已知梯形的中位线长为6㎝，高为4㎝，则此梯形的面积为 ㎝2.
11、有一个直角梯形零件ABCD，AD∥BC，斜腰DC的长为10cm，∠D=120°，则该零件另一AB的长是 cm（结果不取近似值）
12、正n边形的内角和等于1080°，那么这个正n边形的边数n=_____.
13、若一个多边形的内角和是外角和的5倍，则这个多边形是 边形；
14、菱形的一个内角是60º，边长是5cm，则这个菱形的较短的对角线长是 cm；
15、 顺次连接一个任意四边形四边的中点，得到一个四边形 .
16、铺成一片可以不留空隙的平面图形有 （写三个）；
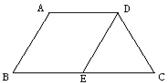17、如图，等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，△DEC的周长是 （ ）
A、3 B、12
C、15 D、19
18、四边形ABCD的对角线AC和BD相交于点O，设有下列条件：①AB=AD；②∠ DAB=900；③AO=CO，BO=DO；④矩形ABCD；⑤菱形ABCD，⑥正方形ABCD，则在下列推理不成立的是 ( )
A、①④
⑥ B、①③⑤ C、①②⑥ D、②③④
19、下列美丽的图案，既是轴对称图形又是中心对称图形的个数是
 |
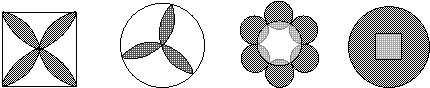（A）1个 （B）2个 （C）3个 （D）4个
20、如图，
ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取什范围是( )
A．1＜m＜11 B．2＜m＜22
C．10＜m＜12 D．5＜m＜6
21、如果要用正三角形和正方形两种图形进行密铺，那么至少需要（ ）
A 三个正三角形，两个正方形 B 两个正三角形，三个正方形
C 两个正三角形，两个正方形 D 三个正三角形，三个正方形
22、如图：矩形花园ABCD中，
，
，花园中建有一条矩形道路LMPQ 及一条平行四边形道路RSTK。若
，则花园中可绿化部分的面积为（ ）
（A）
（B）
（C）
（D）
23、下列图形中只是轴对称图形，而不是中心对称图形的是( )。
A．平行四边形 B．矩形 C．菱形 D．等腰梯形
24、下列命题中，正确命题是（ ）
A．两条对角线相等的四边形是平行四边形；
B．两条对角线相等且互相垂直的四边形是矩形；
C．两条对角线互相垂直平分的四边形是菱形；
D．两条对角线平分且相等的四边形是正方形。
25、观察下面的图形的规律，虚线框内应填入的是
|  | |||
 | |||
 | |||
26、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带( )去配..
A.① B.② C.③ D.①和②
27、使用同一种规格的下列地砖，不能密铺的是 （ ）
A、正六边形地砖 B、正五边形地砖
C、正方形地砖 D、正三角形地砖
28、将一圆形纸片对折后再对折，得到图3，然后沿着图中的虚线剪开，
得到两部分，其中一部分展开后的平面图形是( )
29、如图，E、F、G、H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，四边形ABCD应具备的条件是（ ）.
（A）一组对边平行而另一组对边不平行 （B）对角线相等
（C）对角线互相垂直 （D）对角线互相平分
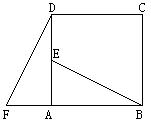30、如图，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=
AB．说明理由：△ABE≌△ADF．
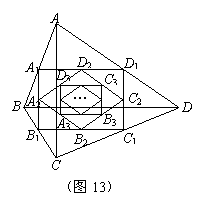31、如图13，四边形ABCD中，AC=6，BD=8且AC⊥BD顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1；再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn .
（1）证明：四边形A1B1C1D1是矩形；
（2）写出四边形A1B1C1D1和四边形A2B2C2D2的面积；
（3）写出四边形AnBnCnDn的面积；
（4）求四边形A5B5C5D5的周长.
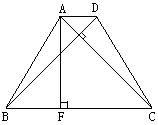
32、用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB，AC重合.将三角尺绕点A按逆时针方向旋转.
（1）当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时，（如图13—1），通过观察或测量BE，CF的长度，你能得出什么结论？并证明你的结论；
（2）当三角尺的两边分别与菱形的两边BC，CD的延长线相交于点E，F时（如图13—2），你在（1）中得到的结论还成立吗？简要说明理由.
33、（6分）如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F。
（1）写出图中每一对你认为全等的三角形；
（2）选择（1）中的任意一对进行证明。
34、已知：如图1，点C为线段AB上的一点，△ACM和△CBN是等边三角形，直线AN、CM交于点E，直线BM、CN交于点F，
求证：（1）AN=BM；（2）△CEF是等边三角形；
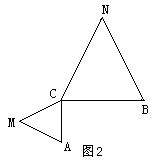（3）将△ACM绕点C按逆时针方向旋转90º，其它条件不变，在图2中补出符合要求的图形，并判断（1）（2）结论是否仍然成立。（不要求证明）
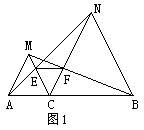
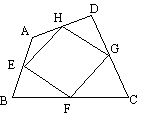
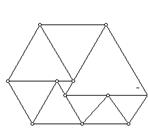35、如图是由9个等边三角形拼成的六边形，现已知中间最小的等边三角形的边长是a，则围成的六边形的周长为
A、30a B、32a C、34a D、无法计算
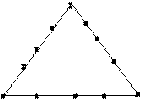
36、现有树12棵,把它栽成三排,要求每排恰好为5棵,如右图所示就是一种符合条件的栽法．请你再给出三种不同的栽法(画出图形即可).
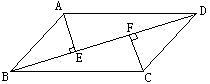
37、（本题满分6分）已知：如图，□ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F. 求证：BE=DF.
38、已知：在△ABC中，AB=AC=a，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q.
(1)求四边形AQMP的周长；
(2)写出图中的两对相似三角形（不需证明）；
(3)M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由.
39、四边形是大家最熟悉的图形之一，我们已经发现了它的许多性质.只要善于观察、乐于探索，我们还会发现更多的结论.
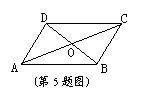
(1)四边形一条对角线上任意一点与另外两个顶点的连线，将四边形分成四个三角形(如图①)，其中相对的两对三角形的面积之积相等.你能证明这个结论吗？试试看.
已知：在四边形ABCD中，O是对角线BD上任意一点（如图①）；
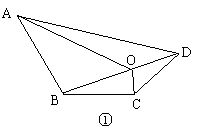求证：S△OBC·S△OAD=S△OAB·S△OCD.
证明：
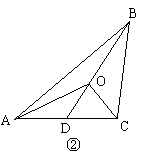(2)在三角形中（如图②），你能否归纳出类似的结论？若能，写出你猜想的结论，并证明：若不能，说明理由.
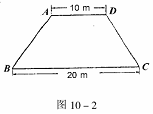
40、某生活小区的居民筹集资金1600元，计划在一块上、下底分别为10m，20m的梯形空地上种植花木（如图10-1）
（1）他们在△AMD和BMC地带上种植太阳花，单价为8元/m2，当△AMD地带种满花后（图10-1中阴影部分），共花了160元，请计算种满△BMC地带所需的费用.
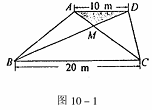
（2）若其余地带要种的有玫瑰和茉莉花两种花木可供选择，单价分别为12元/m2和10元/m2，应选择种哪种花木，刚好用完所筹集的资金？（3）若梯形ABCD为等腰梯形，面积不变（如图10-2），请你设计一种花坛图案，即在梯形内找到一点P，使得△APB≌△DPC且S△APD= S△BPC，并说出你的理由.
