漳州市2003-2004学年上学期期末考试
八年级数学期末考试卷（实验区）
一、 细心想一想，请你把空缺补齐（每空2分，共24分）
1、不等式
的解集为__________；
2、计算
__________；
3、在◇ABCD中，∠A=800，则∠B=__________；
4、把“a的3倍不小于b的
”用不等式表示为____________________；
5、正方形是对角线_______________的矩形；
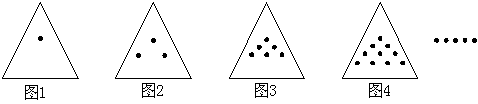
6、找规律：请认真观察下列图形，根据你的推测，图6的图形中共有___点；
7、
恰好是一个完全平方式，则m=__________；
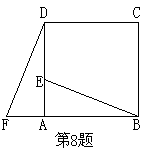
8、如图，在正方形ABCD中，点E是AD的中点，点F是BA延长线上的一点，AF=
AB，△ABE可能通过绕A点逆时针方向旋转到△ADF的位置，则旋转的最小角度为__________度。
9、菱形的两对角线长分别为2cm，3cm，则菱形面积是__________cm2；
10、 平行四边形ABCD的周长为40cm，则AB+BC=__________cm；
11、 当a是负数时，5a__________2a；（“>”、“<”、“=”）
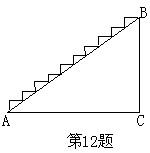
12、 如图，某建筑物BC直立于水平地面，BC=5米，AC=8米，要在阶梯上从A处铺地毯至B处，则至少需地毯__________米。
二、 细心挑一挑选一选，小心不要选错呀！（每题3分，共18分）
13、下无命题正确的是（ ）
A、矩形的对角线互相垂直
B、菱形的对角线相等
C、正方形的对角线相等且互相垂直
D、等腰梯形的底角相等
14、等边三角形能经过旋转与自身重合，至少需要旋转（ ）
A、300 B、1800 C、600 D、1200
15、不等式组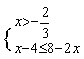
的最小整数解为（ ）
A、-1 B、0 C、1 D、4
16、下列多项式能用公式法进行因式分解的是（ ）
A、
B、
C、
D、
17、已知梯形ABCD中，对角线AC、BD相交于O，则图中面积相等的三角形共有（ ）
A、1对 B、2对 C、3对 D、4对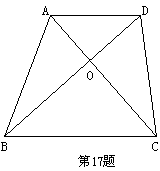
18、下列计算正确的是（ ）
A、
B、
C、
D、
三、 算一算，可别算错哟！（每题4分，共24分）
19、（4分）解不等式，并把它的解集在数轴上表示出来；
20、（4分）计算：
（1）
（2）
21、（4分）因式分解：
22、（4分）阅读：下面是小华同学解不等式组的解答过程：
解：①+②得
x>10
问：小华同学的解答过程是否正确？如果正确，请在数轴上表示其解集，若不正确，请写出正确的解答过程。
四、 学过的知识常会用上，瞧，机会来了，试试你的身手，相信你会成功的。
23、（6分）如图，已知矩形ABCD；
（1） 画出矩形AB’C’D’，使矩形AB’C’D’和矩形ABCD关于A成中心对称；
（2） 边结BD’，D’B’，B’D，DB问四边形BDB’D’是什么形状的四边形？并说明理由。
24、（5分）两人同做一个实验：抛掷一枚图钉，看看钉尖触地的机会有多大，甲做了500次，乙做了800次，甲的结论是：钉尖触地的机会是45.8%；乙的结论是钉尖触地的机会是46.2%，有人说他们得到的结论不一样，所以这种用实验的方法来估计钉尖触地的机会大小是不可取的，你同意他的说法法？请说明理由。
25、（7分）某公园的门票是每位10元，20人以上（含20人）的团体票8折优惠，现在有18们游客买20人的团体票，问比买普通票总共便宜多少钱？此外，不足20人时，至少多少人买20人的团体票才能比普通票便宜？
26、（8分）某工人现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品，共50件，已知生产一件A种产品，需用甲种原料9千克，乙种原料3千克，可获得利润700元；生产一件B种产品，需用甲种原料4千克，乙种原料10千克，可获利润1200，
（1） 按要求安排A、B两种产品的生产件数，有哪几种方案请你设计出来。
（2） 设生产A、B两件产品获总利润y（元），其中一种的生产件数为x，试用含x的代数式表示y，并说明y的取值范围。
（3） （1）中哪种生产方案获总利润最大？最大利润是多少？
27、（8分）将四个如图（1）所示的直角三角形经过平移，旋转对称等变换运动，拼成如图（2）所示的图形，如果连结AD，就可以得到直角梯形ACED（如图3）
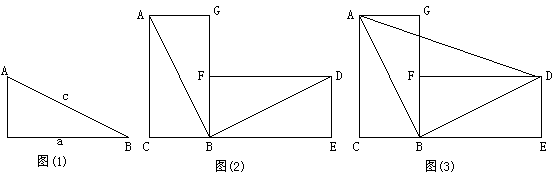
（1）
请结合图（3）说明等式
成立，并用适当的文字叙述这个结论。
（2）
你能拼出其它形状的图形来证明等式成立吗？能拼几种？（只证明其中一种）
（3） 如果上述Rt△ABC的a=5，b=12，你能算出斜边c的值吗？斜边上的高又是多少呢？