八年级（上）数学期末测试题
一、选择题（每小题3分，共36分）
1、
的立方根是（ ）
Ａ.４ Ｂ.２ Ｃ.±４ Ｄ.±２
2、若
、
、
三点都在函数
＜０
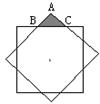
的图象上，则
、
、
的大小关系为（ ）
Ａ、＞＞ Ｂ、＞＞ C、＞＞ D、＞＞
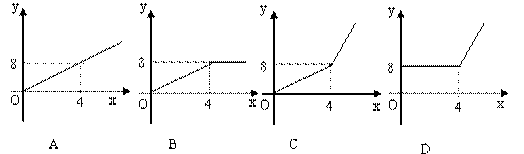
3、2004年6月3日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标民准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水
立方米,水费为
元,则与的函数关系用图象表示正确的是（ ）
 |
4、矩形ABCD中的顶点A、B、C、D按顺时针方向排列,若在平面直角坐标系内, B、D 两点对应的坐标分别是（2, 0）, (0, 0),且 A、C两点关于x轴对称.则C 点对应的坐标是（ ）
A、（1, 1） B、（1, －1） C、（1, －2） D、（, －）
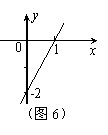
5、已知一次函数y=kx+b的图象（如图6），当x＜0时，y的取值范围是（ ）
A、y＞0 B、y＜0 C、
2＜y＜0 D、y＜2
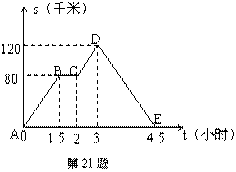
6、如图中的图象（折线ABCDE）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为
千米/时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有（ ）
A、1个 B、2个 C、3个
D、4个
7、某人到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设无缝地板，他购买的瓷砖形状不可以是（ ）
A、正三角形 B、矩形 C、正八边形 D、正六边形
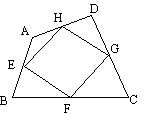
8、如图，E、F、G、H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，四边形ABCD应具备的条件是（ ）.
A、一组对边平行而另一组对边不平行 B、对角线相等
C、对角线互相垂直 D、对角线互相平分
9、为筹备班级的初中毕业联欢会，班长对全班学生爱吃哪几种水果作了民意调查．那么最终买什么水果，下面的调查数据中最值得关注的是（ ）
A、中位数 B、平均数 C、众数 D、加权平均数
10、如图，两块完全重合的正方形纸片，如果上面的一块绕正方形的中心O左0°~90°的旋转，那么旋转时露出的△ABC的面积（S）随着旋转角度（n）的变化而变化，下面表示S与n关系的图象大致是（ ）
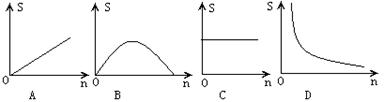
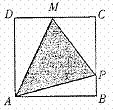
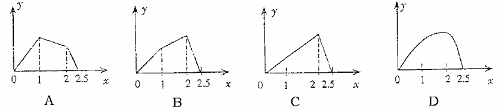11、如图，点P按A→B→C→M的顺序在边长为1的正方形边上运动，M是CD边上的中点.设点P经过的路程x为自变量，△APM的面积为y，则函数y的大致图像是（ ）
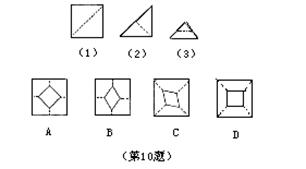
12、小强拿了一张正方形的纸如图（1），沿虚
线对折一次得图（2），再对折一次得图（3），
然后用剪刀沿图（3）中的虚线（虚线与底
边平行）剪去一个角，再打开后的形状应是( )
二、填空题（每小题3分，共24分）
1、已知三角形的三边长为5、12、13，则此三角形的面积为 。
2、已知二元一次方程组
的解也是方程7mx-4y= -18x的解，那么m= 。
3、点M（3，a）在直线y=-x上，若点M向右平移3个单位得点N, 则N点坐标是 。
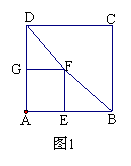
4、如图2，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是_______.
5、某商场在促销期间规定：商场内所有商品按标价的80%出售，同时，当顾客在该商场内消费满一定金额后，按如下方案获得相应金额的奖券.（奖券购物不再享受优惠）
| 消费金额x的范围（元） | 200≤x<400 | 400≤x<500 | 500≤x<700 | … |
| 获得奖券的金额（元） | 30 | 60 | 100 | … |
根据上述促销方法，顾客在该商场购物可获得双重优惠，如果胡老师在该商场购标价450元的商品，他获得的优惠额为_________元.
6、 如图，已知图中每个小方格的边长为1，则点C到AB所在直线的距离等于 。
7、小明在一个学期的数学测试成绩如下：
| 单元1 | 单元2 | 单元3 | 期中 | 期末 |
| 84 | 90 | 78 | 90 | 87 |
如果平时成绩按3次单元平均成绩计，学期成绩按平时、期中、期末各占30%、30%和40%计，小明的数学成绩是 分
8、如图，AD、AE是正六边形的两条对角线，不添加任何辅助线，请写出两个正确的结论：
（1）
；
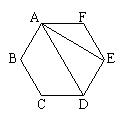（2） ______________。（只写出两个你认为正确的结论即可）
三、解答题（共60分）
1、
2、
21、
22、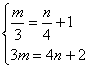
12．如图，正方形纸片ABCD的BC边上有一点E，AE=10㎝．若把纸片沿AE的中垂线折叠，使点E与点A重合，你能求出纸片上折痕MN的长吗？解释你的方法．
 |
21．（本小题满分9分）
甲、乙两件服装的成本共500元，商店老板为获取利润，决定将甲服装按50﹪的利润定价，乙服装按40﹪的利润定价。在实际出售时，应顾客要求，两件服装均按9折出售，这样商店共获利157元，求甲、乙两件服装的成本各是多少元？
20、(本题满分10分)
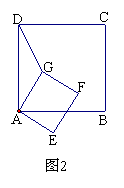
已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
 |  | ||
1.
（本小题满分12分）
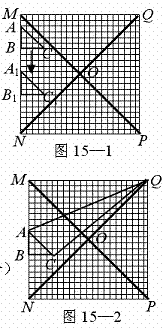
如图15—1和15—2，在20×20的等距网格（每格的宽和高均是1个单位长）中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动.设运动时间为x秒，△QAC的面积为y.
（1）如图15—1，当Rt△ABC向下平移到Rt△A1B1C1的位置时，请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形；
（2）如图15—2，在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？
（3）在Rt△ABC向右平移的过程中，请你说明当x取何值时，y取得最大值和最小值？最大值和最值分别是多少？为什么？
（说明：在（3）中，将视你解答方法的创新程度，给予1~4分的加分）
。
四、探究与思考
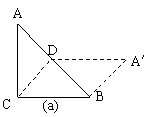
17．（1）如图，把一个等腰直角三角形ABC沿斜边上的高CD（裁剪线）剪一刀，从这个三角形中裁下一部分，与剩下部分能拼成一个四边形A′BCD（见示意图a）．
（以下有画图要求的，工具不限，不必写画法和证明)
①猜一猜：四边形A′BCD一定是 形；
②试一试：按上述的裁剪方法，请你拼一个与图（a）形状不同的四边形，并在图（b）中画出示意图．
 |  | ||
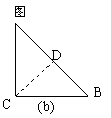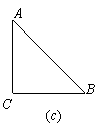
（2）在等腰直角三角形ABC中，请你找出与（1）不同的裁剪线，把分割成的两部分拼成特殊四边形．
①想一想：你能拼得的特殊四边形有 ；
②画一画：请在图（c）中画出一个你拼得的特殊四边形示意图．
 |