全等三角形练习卷2
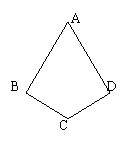
1、如图， AB⊥BC，AD⊥DC，且AD=AB ， 求证：BC=DC
 |
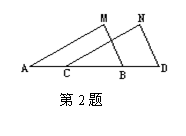2．已知：点 A、C、B、D在同一条直线，AC=BD，AM∥CN，BM∥DN．
求证： AM=CN ，MB=ND。
 |
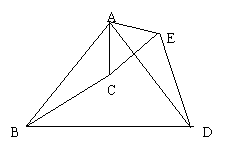3、如右图，AB＝AD ，∠BAD＝∠CAE，AC=AE ，求证：AB=AD
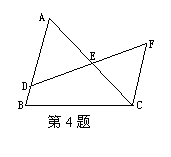4．已知： D是△ABC的边AB上一点，DE交AC于点E，DE=FE，FC∥AB． 求证：AE=CE．
5．已知：△ABC中，∠A是锐角，AB=AC，AC、AB边上的高分别为BE、CF．
求证：BE=CF．(画出图形并证明)
6、如图，AD是△ABC中BC边上的中线，BF⊥AF，CE⊥AD求证：BF=CE
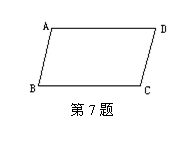
7、已知：如图，AB＝CD，AD＝BC．求证： AB∥DC，AD∥BC
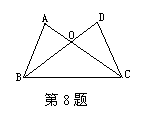8．已知：△ABC和△DBC的顶点A和D在BC的同旁，AB=DC，AC=DB，AC和DB相交于点O．
求证：(1) ∠ABC＝∠DCB (2)OA=OD．
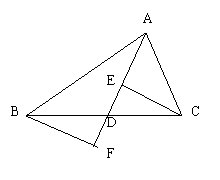
﹡9．已知：如图，AB=AC，FB=FC．F是AD的延长线上一点．求证：DB=DC．
|
﹡10．已知：如图，AB=AC，EB=EC，AE的延长线交BC于D．
求证：BD=CD．
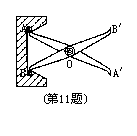11．如图，把两根钢条AA′、BB′的中点连在一起，可以做成一个测量工件内槽宽的工具(卡钳) ，说出其中的道理来。
按图写出“已知”、“求证”，并证明AB=A′B′．
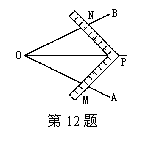
12．工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M、N重合．过角尺顶点P的射线OP便是∠AOB的平分线．根据做法，结合图形写出已知、求证、证明
 |
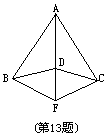
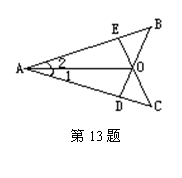13、已知：如图，在AB、AC上各取一点E、D，使AE=AD．连结BD、CE相交于点O，连结AO，∠1=∠2．
求证：① △AOE≌△AOD ②∠B=∠C
14、 如图，欲计算河中礁石（A点）离岸边B点的距离，采用方法如下：顺河取一线段BC，作∠CBA¹=∠CBA，∠BCA¹=∠BCA，则A¹B的长即A到B的距离。请说明理由。
写出已知、求证，并证明。
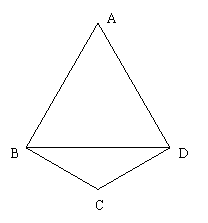
15、如图，已知AB⊥AC，BD⊥DC，且AB=DC ， 求证：①AC=DB ②AO=DO
 | |||
 | |||
﹡16、已知AB⊥AC，AD⊥DC，且BC=DC ， 求证：∠ABD＝∠ADB
17、：如图，AD∥BC 且AD＝BC，AE=CF，
求证：①AB=DC ②EB=DF