初中毕业班数学第一次调研考试
数 学 试 题
一、选择题（每小题3分,共24分）
1.若二次根式
有意义,则实数
的取值范围为…………………………………………（ ）
A、
B、
C、
D、
2.抛物线
的顶点坐标是………………………………………………………（ ）
A、
B、
C、
D、
3.已知
的半径为3㎝,
的半径为4㎝,且圆心距
与的位置关系是…………………………………………………………………………………………………（ ）
A、外离 B、外切 C、相交 D、内含
4.方程
的根为………………………………………………………………（ ）
A、
B、
C、
D、
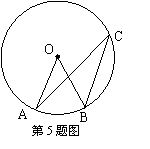
5.如图,点A、B、C在
上,AO∥BC,∠OBC=40°，则∠ACB的度数是……………………（ ）
A、10° B、20° C、30° D、40°
 | |||||
 | |||||
 | |||||
6.反比例函数
的图象位于……………………………………………（ ）
A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限
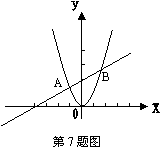
7.如图,一次函数
与二次函数
交于
和
两点,则当
的取值范围是………………………………………………………………………………………（ ）
A、
B、
C、
D、
8.如图,是在纸上剪下的一个圆形和一个扇形的纸片,若它们恰好能围成一个圆锥模型,圆的半径为
,扇形的半径为R,扇形的圆心角等于90°,则与R之间的关系是………………………（ ）
A、
B、
C、
D、
二、填空题（每小题3分,共18分）
9.根据下面的运算程序,若输入
时,输出的结果
_________________________.
 |
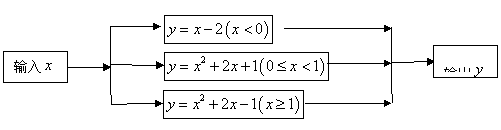10.从
这三个数中任取两个不同的数作二次函数
中的b、c，所得二次函数的图象一定经过原点的概率是_________________________.
11.若关于的一元二次方程
有两个不相等的实数根,则
的取值范围是_________________________.
12.若
的值是整数,则自然数
的值为_________________________.
13.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A（2，3）、B（2，1）、C（3，2）,如果△ABC沿着边AB旋转,则所得旋转体的体积是_________________________.（结果保留
）
 | |||
 | |||
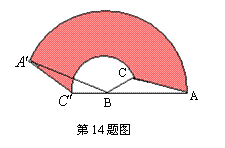14.如图,在△ABC中,AB=8㎝,BC=4㎝,∠ABC=30°，把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的
处,那么AC边扫过的图形（图中阴影部分）的面积是_________________________
.（结果保留）
三、解答题（共78分）
15.（5分）计算 
16.（5分）解方程 
17.（5分）已知
的值.
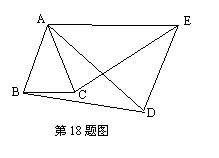
18.（6分）如图,等腰△ABC和等腰△ADE的顶角∠BAC=∠DAE=30°，△ACE可以看作是△ABD经过什么图形变换得到的？说明理由.
 |
19.（6分）已知二次函数
的图象与轴交于A、B两点,且经过C（1，－2）,求点A、B的坐标和
的值.
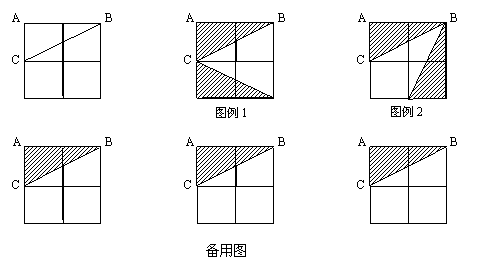
20.（6分）如图是2×2的方格,在格点处有一个△ABC,仿照图例在备用图中画出三种与△ABC成轴对称的“格点三角形”.
 |
21.（7分）定理：若
、
是关于的一元二次方程
的两实根,则有
，
.请用这一定理解决问题：已知、是关于的一元二次方程
的两实根,且
，求
的值.
22.（8分）小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪个人先下棋,规则如下：
三人手中各持有一枚质地均匀的硬币,他们同时将手中硬币抛落到水平地面为一个回合,落地后,三枚硬币中,恰有两枚正面向上或者反面向上的两人先下棋；若三枚硬币均为正面向上或反面向上,则不能确定其中两人先下棋.
（1）请你完成下面表示游戏一个回合所有可能出现的结果的树状图；
（2）求出一个回合能确定两人下棋的概率.
解：（1）树状图为：
23.（8分）如图,已知的直径AB垂直弦CD于点E,过C点作CG∥AD交AB延长线于点G,连结CO并延长交AD于点F,且CF⊥AD.
（1）求证：CG是⊙O的切线；
（2）若AB=4,求CD的长.
24.（10分）宏达纺织品有限公司准备投资开发A、B两种新产品,通过市场调研发现：如果单独投资A种产品,则所获利润（万元）与投资金额（万元）之间满足正比例函数关系：
；如果单独投资B种产品,则所获利润（万元）与投资金额（万元）之间满足二次函数关系：
.根据公司信息部的报告,
（万元）与投资金额（万元）的部分对应值（如下表）
|
_________________________；
_________________________；
（2）如果公司准备投资20万元同时开发
A,B两种新产品,请你设计一个能获得最大利润
的投资方案,并求出按此方案能获得的最大利润是多少万元？
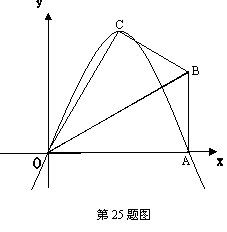
25.（12分）已知：在Rt△ABO中,∠OAB=90°,∠BOA=30°,AB=2,若以O为坐标原点,OA所在直线为轴,建立如图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处.
（1）求点C的坐标；
（2）若抛物线
经过C、A两点,求此抛物线的解析式；
（3）若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作
轴的平行线,交抛物线于点M,问：是否存在这样的点P,使得四边形CDPM为很等腰梯形？若存在,请求出此时点P的坐标；若不存在,请说明理由.
参考答案
一、选择题BCCABCDD
二、填空题9.2；10.
；11.
；12.
；13.
；14.
三、解答题
15.
；16.
；17.
18.解：△ACE可以看作是△ABD以A点为中心逆时针旋转30°得到的,其理由如下：
∵∠BAC=∠DAE,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△ABD≌△ACE（SAS）
又一对对应边AB与AC的夹角为30°,∴△ACE可以看作是△ABD以A点为中心逆时针旋转30°得到的.
19.解：令
,得
，∵
，∴
∴A（－1，0），B（3，0），再将点C的坐标代入函数式可得：
20. （略）
21.解：由已知定理得：
，
∴
,
即
，解得：
,
当
时,△=
，∴舍去.
当
时, △=
，∴的值为1.
22.（1）略；（2）由（1）树状图可知：
.
23.（1）略；（2）连结AC,可得CE
；从而CD=2CE=
.
24.（1）
,
（2）设投资万元生产B产品,则投资
万元生产A产品,共获得利润W万元,则
,
答：投资6万元生产B产品,14万元生产A产品可获得最大利润19.2万元.
25.（1）点C（
）；（2）抛物线的解析式为：
（3）存在,此时点P为
.