初中毕业考试数学试卷
(全卷三个大题,共25个小题;考试时间120分钟;满分:120分)
| 题 号 | 一 | 二 | 三 | 总 分 |
| 得 分 |
注意:考生可将《2008年云南省高中(中专)招生考试说明与复习指导·数学手册》及科学计算器(品牌和型号不限)带入考场使用.
| 得分 | 评卷人 |
|
|
|
一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分)
1.-2的倒数是( )
A.![]() B.
B.![]() C. 2 D.-2
C. 2 D.-2
2.下列运算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.下图中所示的几何体的主视图是( )
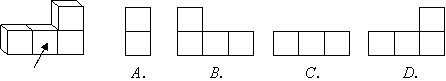 |
4.不等式组![]() 的解集为( )
的解集为( )
A.x>2 B.x<3
C.x>2或 x<-3 D.2<x<3
5.下列事件是必然事件的是( )
A.今年6月20日双柏的天气一定是晴天
B.2008年奥运会刘翔一定能夺得110米跨栏冠军
C.在学校操场上抛出的篮球会下落
D.打开电视,正在播广告
 6.圆锥侧面展开图可能是下列图中的( )
6.圆锥侧面展开图可能是下列图中的( )
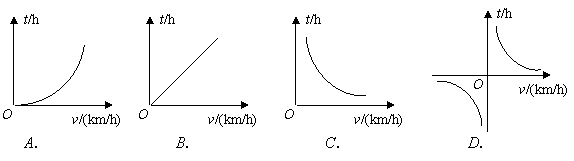
7.已知甲、乙两地相距![]() (km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间
(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间![]() (h)与行驶速度
(h)与行驶速度![]() (km/h)的函数关系图象大致是( )
(km/h)的函数关系图象大致是( )
 |
8.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是( )
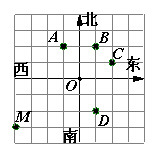 A.点A
A.点A
B.点B
C.点C
D.点D
| 得分 | 评卷人 |
|
|
|
二、填空题(本大题共7个小题,每小题3分,满分21分)
 9.分解因式:
9.分解因式:![]() .
.
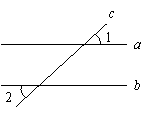
10.如图,直线![]() 被直线
被直线![]() 所截,
所截,
若![]() ,
,![]() ,则
,则![]()
![]() .
.
11.双柏鄂加老虎山电站年发电量约为156亿千瓦时,用科学记数法表示156亿千瓦时= 千瓦时.
12.函数![]() 中,自变量
中,自变量![]() 的取值范围是
.
的取值范围是
.
13.为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1和图2,请在图1中将“乒乓球”部分的图形补充完整.
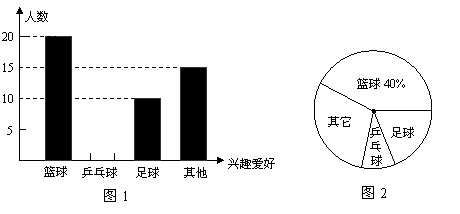 |
14.下面是一个简单的数值运算程序,当输入![]() 的值为2时,输出的数值是
.
的值为2时,输出的数值是
.
 |
15.如图,点![]() 在
在![]() 的平分线上,若使
的平分线上,若使![]() ,
,
则需添加的一个条件是 .
(只写一个即可,不添加辅助线)
| 得分 | 评卷人 |
|
|
|
三、解答题(本大题共10个小题,满分75分)
| 得分 | 评卷人 |
16.(本小题6分)先化简,再求值:
![]() ,其中
,其中![]() .
.
| 得分 | 评卷人 |
17.(本小题6分)解分式方程:![]() .
.
| 得分 | 评卷人 |
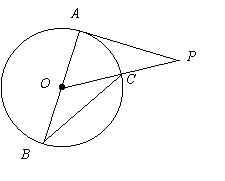
18.(本小题6分)![]() 是⊙O的直径,
是⊙O的直径,![]() 切⊙O于
切⊙O于![]() ,
,![]() 交⊙O于
交⊙O于![]() ,连
,连![]() .若
.若![]() ,求
,求![]() 的度数.
的度数.

| 得分 | 评卷人 |
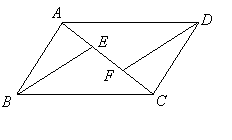
19.(本小题8分)如图,![]() 是平行四边形
是平行四边形![]() 的对角线
的对角线![]() 上的点,
上的点,![]() . 请你猜想:
. 请你猜想:![]() 与
与![]() 有怎样的位置关系和数量关系?并对你的猜想加以证明.
有怎样的位置关系和数量关系?并对你的猜想加以证明.
猜想:
 证明:
证明:
| 得分 | 评卷人 |
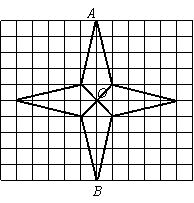
20.(本小题6分)如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:
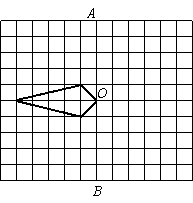 |
(1)作出关于直线AB的轴对称图形;
(2)将你画出的部分连同原图形绕点
O逆时针旋转![]() ;
;
(3)发挥你的想象,给得到的图案适
当涂上阴影,让它变得更加美丽.
| 得分 | 评卷人 |
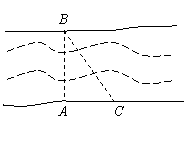
21.(本小题6分)根据“十一五”规划,元双(双柏—元谋)高速工路即将动工.工程需要测量某一条河的宽度.如图,一测量员在河岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得![]() .求所测之处河AB的宽度.
.求所测之处河AB的宽度.
 (
(![]() )
)
| 得分 | 评卷人 |
22.(本题8分)一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中任意摸出一个球是白球的概率是多少?
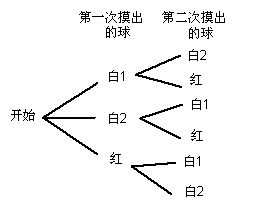
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出的球都是白球的概率,并画出树状图.
| 得分 | 评卷人 |
23.(本小题8分)我县农业结构调整取得了巨大成功,今年水果又喜获丰收,某乡组织30辆汽车装运A、B、C三种水果共64吨到外地销售,规定每辆汽车只装运一种水果,且必须装满;又装运每种水果的汽车不少于4辆;同时,装运的B种水果的重量不超过装运的A、C两种水果重量之和.
(1)设用x辆汽车装运A种水果,用y辆汽车装运B种水果,根据下表提供的信息,求y与x之间的函数关系式并写出自变量的取值范围.
| 水果品种 | A | B | C |
| 每辆汽车运装量(吨) | 2.2 | 2.1 | 2 |
| 每吨水果获利(百元) | 6 | 8 | 5 |
(2)设此次外销活动的利润为Q(万元),求Q与x之间的函数关系式,请你提出一个获得最大利润时的车辆分配方案.
| 得分 | 评卷人 |
24.(本小题9分)依法纳税是每个公民应尽的义务.从2008年3月1日起,新修改后的《中华人民共和国个人所得税法》规定,公民每月收入不超过2000元,不需交税;超过2000元的部分为全月应纳税所得额,都应纳税,且根据超过部分的多少按不同的税率纳税,详细的税率如下表:
| 级别 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过500元的 | 5 |
| 2 | 超过500元至2 000元的部分 | 10 |
| 3 | 超过2 000元至5 000元的部分 | 15 |
| 4 | 超过5 000元至20 000元的部分 | 20 |
| … | … | … |
(1)某工厂一名工人2008年3月的收入为2 400元,问他应交税款多少元?
(2)设x表示公民每月收入(单位:元),y表示应交税款(单位:元),
当2500≤x≤4000时,请写出y关于x的函数关系式;
(3)某公司一名职员2008年4月应交税款120元,问该月他的收入是多少元?
| 得分 | 评卷人 |
25.(本小题(1)~(3)问共12分;第(4)、(5)问为附加题10分,每小题5分,附加题得分可以记入总分,若记入总分后超过120分,则按120分记)
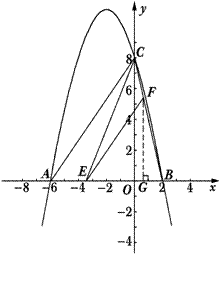
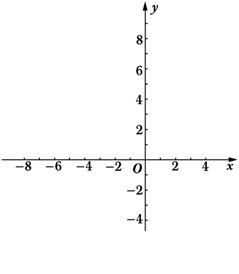
已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)求△ABC的面积;
(4)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(5)在(4)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.

数学试卷参考答案
一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分)
1.A 2.B 3. D 4.D 5.C 6.D 7.C 8.B
二、填空题(本大题共7个小题,每小题3分,满分21分)
9.(x+1)(x-1) 10.60 11.1.56×109 12.x≠3 13.到5
14.0 15.OA=OB或∠OAP=∠OBP或∠OPA=∠OPB
三、解答题(本大题共10个小题,满分75分)
16.(本小题6分)
解:解:原式![]()
![]()
![]()
将![]() 代入上式得
代入上式得
原式![]()
![]()
17.(本小题6分)
解:去分母,得![]()
去括号,移项,合并,得![]()
检验,得![]() 是原方程的根.
是原方程的根.
18.(本小题6分)
![]() 切⊙O于
切⊙O于![]() 是⊙O的直径,
是⊙O的直径,
∴![]() .
.
![]() ,∴
,∴![]() .
.
∴![]() .
.
 19.(本小题8分)
19.(本小题8分)
猜想:![]() ,
,![]()
证明:
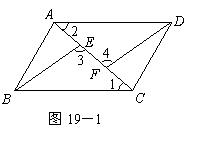
证法一:如图19-1
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
![]()
![]()
又![]()
![]()
![]()
![]()
![]()
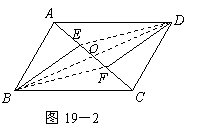
证法二:如图19-2
连结![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() .
.
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]() ,
,![]()
又![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
20.(本小题6分)如图.三步各计2分,共6分.
21.(本小题6分)
解:解:在![]() 中,
中,![]() ,
,
∴![]() (米)
(米)
答:所测之处河的宽度AB约为248米
22.(本题8分)
 解:(1)从箱子中任意摸出一个球是
解:(1)从箱子中任意摸出一个球是
白球的概率是![]()
(2)记两个白球分别为白1与白2,
画树状图如右所示:从树状图可看出:
事件发生的所有可能的结果总数为6,
两次摸出球的都是白球的结果总数为2,
因此其概率![]() .
.
23.(本小题8分)
解:(1)由题得到:2.2x+2.1y+2(30-x-y)=64 所以 y = -2x+40
又x≥4,y≥4,30-x-y≥4,得到14≤x≤18
(2)Q=6x+8y+5(30-x-y)= -5x+170
Q随着x的减小而增大,又14≤x≤18,所以当x=14时,Q取得最大值,
即Q= -5x+170=100(百元)=1万元。
因此,当x=14时,y = -2x+40=12, 30-x-y=4
所以,应这样安排:A种水果用14辆车,B种水果用12辆车,C种水果用4辆车。
24.(本小题9分)
解:(1)该工人3月的收入2 400元中,应纳税的部分是400元,按纳税的税率表,
他应交纳税款![]() (元);
(元);
(2)当![]() 时,其中2 000元不用纳税,应纳税的部分在500元至2
000元之间,其中500元按
时,其中2 000元不用纳税,应纳税的部分在500元至2
000元之间,其中500元按![]() 交纳,剩余部分按
交纳,剩余部分按![]() 交纳,
交纳,
于是,有![]() ;
;
即![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() .
.
(3)根据(2)可知,当收入为2 500元至4 000元之间时,纳税额在25元至175元之间,于是,由该职员纳税款120元,可知他的收入肯定在2 500元至4 000元之间;
设他的收入为z元,由(2)可得:![]() ,解得:z=3450;
,解得:z=3450;
故该职员2008年4月的收入为3450元.
25.(本小题12分)解:(1)解方程x2-10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=-2
∴由抛物线的对称性可得点A的坐标为(-6,0)
∴A、B、C三点的坐标分别是A(-6,0)、B(2,0)、C(0,8)
(2)∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8,将A(-6,0)、B(2,0)代入表达式y=ax2+bx+8,得
解得
∴所求抛物线的表达式为y=-x2-x+8
(3)∵AB=8,OC=8
∴S△ABC =×8×8=32
(4)依题意,AE=m,则BE=8-m,
∵OA=6,OC=8, ∴AC=10
∵EF∥AC ∴△BEF∽△BAC
∴= 即= ∴EF=
过点F作FG⊥AB,垂足为G,则sin∠FEG=sin∠CAB=
∴= ∴FG=·=8-m
∴S=S△BCE-S△BFE=(8-m)×8-(8-m)(8-m)
=(8-m)(8-8+m)=(8-m)m=-m2+4m
自变量m的取值范围是0<m<8
(5)存在. 理由:
∵S=-m2+4m=-(m-4)2+8 且-<0,
∴当m=4时,S有最大值,S最大值=8
∵m=4,∴点E的坐标为(-2,0)
∴△BCE为等腰三角形.