初三（下）第一次调研测试数学试卷
友情提示：本试卷满分120分，共有五个大题，25个小题，考试时间为120分钟。
亲爱的同学，你好！今天是展示你才能的时候了，只要你仔细审题、认真答题，把
平常的水平发挥出来，你就会有出色的表现，放松一点，相信自己的实力！
（注：班级、学号、姓名请写在每张试卷的左边以便密封，谢谢合作。）
| 题号 | 一 | 二 | 三 | 四 | 五 | 总分 | ||||||
| 12 | 13 | 14 | 15 | 161 | 17 | 18 | 19 | 20 |
| |||
| 得分 |
|
|
|
|
|
|
|
|
|
|
| |
一、选择题（每题4分，共12分）
1、下列事件中是必然事件的是（ ）
A、中秋节晚上能看到月亮 B、今天考试小明能得满分
C、早晨的太阳从东方升起 D、明天气温会升高
2、如果
，则代数式
的值为（ ）
A、6 B、8 C、－6 D、－8
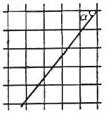3根据图6中的信息，经过估算，下列数值与正方形网格中
∠ɑ的正切值最接近
的是（ ）.
（A）0.6246 （B）0.8121
（C）1.2252 （D）2.1809
二、填空题（每题4分，共32分）
4
5、写出一个解是 X1=2 的一个一元二次方程_________________.
X2=-3
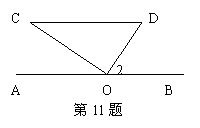
6、将三角板（不是等腰的）顶点放置在直线AB上的O点处，
使AB∥CD，则∠2的余弦值是_____________.
7、抛物线
的顶点坐标是________________
8、若△ABC∽△DEF,且相似比
,当S△ABC=6cm2时,则S△DEF= cm2。
9．如图，
内接于⊙O，
，
，则⊙O的半径为____________
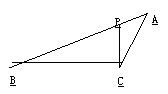
第11题
10.如图，在ΔABC中，P为AB上一点，在下列四个条件中：①∠APC=∠B；②∠APC=∠ACB；
③AC2=AP•AB；④AB•CP=AP•CB，能满足ΔAPC与ΔACB相似的条件是 （只填序号）.
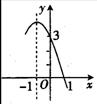
11、抛物线
的部分图象如图所示，若
，则
的取值范围是__________
三、（本大题共4小题，每小题7分,共28分）
12、
sin60°·COS45°+ 
13.解方程：3x2+5x-1=0
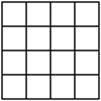14.在方格纸中，每个小格的顶点叫做格点,以格点连线为边的三角
形叫做格点三角形.请你在如图所示的4×4的方格纸中,画出两个
相似但不全等的格点三角形(要求:所画三角形为钝角三角形,标明
字母,).
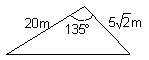
15一块如图所示的三角形地面，现准备种植每平方米售价10元的草皮以美化
环境，则购买这种草皮至少需要多少元？
|
三、（本大题共3小题，每小题8分,共24分）
16、（8分）如图:学校旗杆附近有一斜坡．小明准备测量学校旗杆AB的高度，他发现当
斜坡正对着太阳时，旗杆AB的影子恰好落在水平地面和斜坡的坡面上，此时小明测得水平地面
上的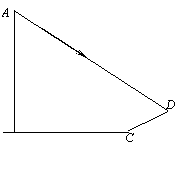
影长 BC=20米，斜坡坡面上的影长CD=8米，太阳光线AD与水平地面成30°角，斜坡
CD与水平地面BC成30°的角，求旗杆AB的高度（精确到1米）．
17、如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形
称为“格点三角形”，图中的△ABC就是格点三
角形。在建立平面直角坐标系后，
点B为（－１，－１）。
（1）把△ABC向左平移8格后得到△
，
则点
的坐标为
；
（2）把△ABC绕点C按顺时针方向旋转90°后得
到△
，则点
的坐标为
；
（3）把△ABC以点A为位似中心放大，使放大前后对应边长的比为1：2，则
的坐标为 ；
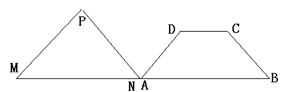
18、如图：在等腰梯形ABCD中，AB∥CD，∠A=60°，AB=20cm，CD=8cm。等边三角形PMN的边长
MN=20cm，A点与N点重合，MN和AB在一条直线上，设等腰梯形ABCD不动，等边三角形PMN沿
AB所在的直线匀速向右移动，直到点M与点B重合为止。
（1）等边三角形PMN在整个运动过程中与等腰梯形ABCD重叠部分的形状由 形变
为 形，再变为 形；
（2）设等边三角形移动距离x（cm）时，等边三角形PMN与等腰梯形ABCD重叠的部分的面积
为y，求y与x之间的函数关系式；
五、综合题（每题12分，共24分）
24、（12分）如图,平面直角坐标系中,直线AB与轴,
轴分别交于A(3,0),B(0,
)
两点, ,点C为线段AB上的一动点,过点C作CD⊥轴于点D.
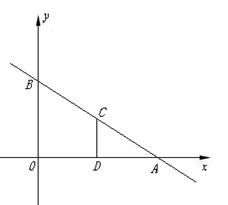(1)求直线AB的解析式;
(2)若S梯形OBCD＝
,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的三角形与△OBA相似.若存
在,请求出所
有符合条件的点P的坐标;若不存在,请说明理由.
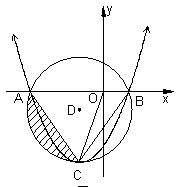
25、已知：如图，抛物线
的顶点C在以D（―2，―2）为圆心，
4为半径的圆上，且经过⊙D与轴的两个交点A、B，连结AC、BC、OC。
（1）求点C的坐标； （2）求图中阴影部分的面积；
（3）在抛物线上是否存在点P，使DP所在直线平分线段OC？若存在，求出点
P的坐标；若不存在，请说明理由。
参考答案
一、1、C 2、C 3、D 4、C 5、D 6、C 7、D 8、C
二、9、1 10、略 11、
12、（2，0） 13、24 14 、4 15、②③ 16、-3﹤X﹤1
三、17、
（每对一个知识点给1分） 18、略 19、略
20、S⊿=50 W=500元 21、20
22、（1）（-9，-1）（2）（5，5）（3）（-5，-5）或（5，5）（每问2分，第3问答对一个就给2分）
23、（1）等边三角形、等腰梯形、等边三角形----------2分
（2）
下结论1分。
27、（1）直线AB解析式为：y=
x+．
（2）∵ 
,
＝
，∴
由OA=OB，得∠BAO＝30°，AD=CD．
∴ 
＝CD×AD＝
＝
．可得CD＝
．
∴ AD=１，OD＝２．∴C（２，）．
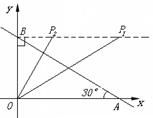
（3） 当∠OBP＝Rt∠时，如图
①若△BOP∽△OBA，则∠BOP＝∠BAO=30°，BP=OB=3，∴
（3，）．
②若△BPO∽△OBA，则∠BPO＝∠BAO=30°,OP=OB=1．∴
（1，）．
当∠OPB＝Rt∠时
③ 过点P作OP⊥BC于点P(如图)，此时△PBO∽△OBA，∠BOP＝∠BAO＝30°
过点P作PM⊥OA于点M．
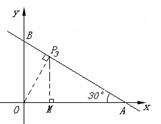设Ｐ（x ，x+），得OM＝x ，PM＝x+
由∠BOP＝∠BAO,得∠POM＝∠ABO．
=
=
=．
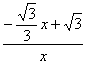∴x+＝x，解得x＝
．此时，
（，
）．
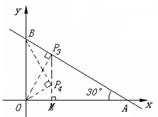
④若△POB∽△OBA(如图)，则∠OBP=∠BAO＝30°，∠POM＝30°．
∴ PM＝OM＝
．∴ 
（，）（由对称性也可得到点的坐标）．当∠OPB＝Rt∠时，点P在ｘ轴上,不符合要求.综合得，符合条件的点有四个，分别是：
（3，），（1，），（，），（，）．
25．解：（1）如图，作CH⊥轴，垂足为H，
∵直线CH为抛物线对称轴，∴H为AB的中点。…1分
∴CH必经过圆心D（―2，―2）。∵DC=4，∴CH=6 ∴C点的坐标为（―2，―6）。 …4分
（2）连结AD，在Rt△ADH中，AD=4，DH=2，∴
，
。。。6分
∴
∴
∴阴影部分的面积
。。。。。。。8分
（3）又∵
，H点坐标为（―2，0），H为AB的中点，
∴A点坐标为（―2―2
，0），B点坐标为（
，0）。
………9分
又∵抛物线顶点C的坐标为（―2，―6），设抛物线解析式为
∵B（，0）在抛物线上， ∴
，解得
。
∴抛物线的解析式为
…………………………10分
设OC的中点为E，过E作EF⊥轴，垂足为F，连结DE，
∵CH⊥轴，EF⊥轴，∴CH∥EF ∵E为OC的中点，∴
。
即点E的坐标为（―1，―3）。 设直线DE的解析式为
，
∴
，解得
，∴直线DE的解析式为
。 ……………11分
若存在P点满足已知条件，则P点必在直线DE和抛物线上。 设点P的坐标为（
，
），
∴
，即点P坐标为（，
）， ∴
，
解这个方程，得
，
∴点P的坐标为（0，－4）和（－6，2）。 ……12分