08年北京市中考模拟分类汇编（2）
方程与不等式
1.方程
⑴ 解方程
1.
（海淀一模）用求根公式解方程
.
【答案】
.
2.
(丰台一模)解方程：
．
【答案】去分母，得 
， …………………
分
去括号，得 
，………………
分
解方程，得 
．…………………………………
分
经检验：是原方程的解．………………………
分
∴ 原方程的解为．
3.
（宣武一模）解方程：
.
【答案】
. ………………………………………… 2分
. …………………………………………………… 3分
.
.
. …………………………………………………… 4分
经检验，是原方程的解. ……………………………………………………… 5分
4.
（大兴一模）解方程方程：
【答案】
5.
（朝阳一模）解方程：
．
【答案】
方程两边同时乘以
，得
，…………………………………………2分
，
． ………………………………………………………4分
经检验：是原方程的解．……………………………………………5分
6.
（石景山二模）解方程组：
【答案】
由方程（2），得
（3） ………………………………1分
把（3）代入（1），得
，解得
； ……………………3分
把代入（3），得.
…………………………………4分
所以，原方程组的解是
…………………………5分
⑵ 一元二次方程的性质
1. （昌平二模）已知3是关于x的方程 x２-3a+1=0 的一个根，则1-3a的值是（ B ）
A. -10 B. - 9 C. -3 D. -11
2.
（海淀一模）已知一元二次方程
，则这个方程的根的情况为（ ）
A.有个不等实数根 B.有两个相等的实数根 C.没有实数根 D.不能确定
【答案】 选C.
3.
(丰台一模)若方程
有两个不相等的实数根，则
的取值范围是( D )
A．
B．
C．
D． 
4.
（大兴一模） –若关于x的一元二次方程
没有实数根，则实数m的取值范围是（C ）
A．m<l B．m>-1 C．m>l D．m<-1
5.
（宣武一模））为何正整数时，关于
的一元二次方程
有两个不相等的实数根.
【答案】
. …………………………………………… 2分
要使方程有两个不相等的实数根，必须有
，
即
，
………………………………………………………………… 4分
为正整数，
1、2、3、4. ………………………………………………………………………… 5分
⑵ 方程的应用
6. （海淀一模）小明家在装修房子使用同样规格的黑白两色的正方形瓷砖铺设矩形的露天平台，根据不同的地块设计了两种不同的方案，设计的图纸如示意图（外面一周都设计为黑色瓷砖）.
如果有一块地方小明用其中一种方案铺设，共用了1056块瓷砖，问这块地方使用的是哪种设计方案，请你给出解答过程.
【答案】 据观察可知两种方案中，长比宽多出一块瓷砖，
则可设宽用
块，长需用
块，
列方程
，解得
（不合题意，舍去），
观察两种方案的规律得知只有方案一的宽为偶数，长为奇数，
∴应该选择方案一.
7.
（朝阳一模）列方程（组）解应用题：
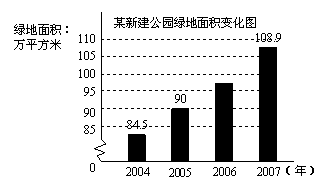
某新建公园的绿化给公园自身及周边的环境都带来了明显的改变，右面的条形图是这个新建公园近几年来绿地面积的变化图，请你根据图中所给的数据解答下列问题：
⑴ 求这个公园
年底至
年底这两年绿地面积的年平均增长率；
⑵ 根据这个平均增长率，请你预测
年底这个公园的绿地面积将达到多少万平方米？
【答案】
⑴ 设这两年底绿地面积年平均增长率为．……………………………………1分
依题意,得 
.……………………………………………2分
解得
，
（不符合题意舍去）.…………………………3分
∴
.
答:这两年底绿地面积年平均增长率为
．………………………………4分
⑵ 
．
答：预测年底这个公园的绿地面积将达到
万平方米．……5分
8.
(丰台一模)某小区便利店老板到厂家购进
、
两种香油共
瓶，花去了
元．其进价和售价如下表：
| 进价（元/瓶） | 售价（元/瓶） | |
|
|
|
|
|
|
|
|
（1）该店购进
、
两种香油各多少瓶？
（2）将购进的
瓶香油全部销售完，可获利多少元？
【答案】
⑴ 设购进
种香油瓶，则购进种香油
瓶，…………
分
根据题意，得
， …………………………………分
，解得 
． ……………………………………分
∴ 
．
答：购进、两种香油分别为80瓶、60瓶． …………………………分
⑵ 
(元)．
答：将购进的瓶香油全部销售完可获利240元． ……………………
分
2.不等式
1.
（海淀一模）求解不等式组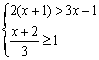
，并在数轴上表示出它的解集.
【答案】
.（数轴上表示的解集略）
2.
（宣武一模）解不等式组
并把解集在数轴上表示出来.
【答案】
解
,得
. …………………………………………………………………1分
解
,得
. ………………………………………………………………3分
. ……………………………………………………4分
解集在数轴上表示如下：
………………………………………………………… 5分
3.
(丰台一模)若
满足不等式组 
请你为选取一个合适的数，使得代数式
的值为一个奇数．
【答案】解这个不等式组，得 
……………………分
∴不等式组的解集为
． ……………………分
………………分
．………………………………分
当
时，原式＝
． …………………………………
分
（或当
时，原式
1．）（说明：取
，原式
，不得分．）
4. （石景山二模）个人发表文章、出版图书所得稿费的纳税计算方法是：（1）稿费不高于800元的不纳税；（2）稿费高于800元而不高于4000元，缴纳超过800元部分稿费的14％；
（3）稿费超过4000元的，缴纳全部稿费的11％．张老师得到一笔稿费，缴纳个人所得税420元，问张老师的这笔稿费是多少元？
【答案】∵ 4000×11％＝440＞420，
∴ 张老师的这笔稿费不超过4000元. ………………………1分
设张老师的这笔稿费为x元，根据题意，得
（x－800）×14％＝420． ………………………3分
解得 x＝3800． ………………………4分
答：张老师的这笔稿费为3800元． ………………………5分