08年北京市中考模拟分类汇编⑶
统计与概率
一、统计
⑴ 平均数、众数、中位数、方差
4.（海淀一模）从申奥成功的2001年开始到2007年，北京市全年空气质量达到二级和好于二级的天数分别为（单位：天）185，203，224，229，227，241，246，则北京这几年全年空气质量达到二级和好于二级的天数的平均值（取整数）约为（ ）天.
A.225 B.222 C.213 D.198
【答案】
.
1. （朝阳一模）要比较两位同学在五次体育测验中谁的成绩比较稳定，应选用的统计量是（ ）
平均数 
中位数 
众数 
方差
【答案】
2. （大兴一模）某制衣厂要确定一种衬衫不同号码的生产数量，在做市场调查时，该商家侧重了解的是这种衬衫不同号码的销售数量的（ ）
A. 平均数 B. 众数
C. 标准差 D. 中位数
【答案】 B
3.
(丰台一模)甲、乙两同学近期5次百米跑测试成绩的平均数相同，甲同学成绩的方差
，乙同学成绩的方差
，则下列对他们测试成绩稳定性的判断，正确的是（ ）
A．甲的成绩较稳定 B．乙的成绩较稳定
C．甲、乙成绩稳定性相同 D．甲、乙成绩的稳定性无法比较
【答案】 B
4. （石景山二模）某青年篮球队12名队员的年龄情况如下表：
| 年龄/岁 | 18 | 19 | 20 | 21 | 22 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
则这12名队员年龄的 （ ）
A．众数是20岁，中位数是19岁
B．众数是19岁，中位数是19岁
C．众数是19岁，中位数是20.5岁
D．众数是19岁，中位数是20岁
【答案】 D
5. （昌平二模）甲、乙两名同班同学的5次数学测验成绩（满分120分）如下：
甲：97，103，95，110，95
乙：90，110，95，115，90
经计算，它们的平均分
=100，
=100；方差是
=33.6，
=110，则这两名同学在这5次数学测验中成绩比较稳定的是
同学.
【答案】 甲
6.
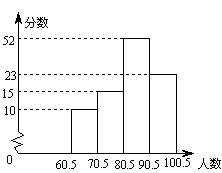
（朝阳一模）为了让学生知道更多的奥运知识，某中学举行了一次“奥运知识竞赛”．为了解这次竞赛成绩情况，抽取部分学生成绩（成绩取整数，满分为
分）作为样本，绘制了如下的直方图，请结合此图回答下列问题：
⑴ 此样本抽取了多少名学生的成绩？
⑵ 此样本数据的中位数落在哪一个范围内？
⑶ 若这次竞赛成绩
分以上（不含分）的学生可获奖，请估计获奖人数占参赛总人数的百分比是多少？
【答案】
方程两边同时乘以
，得
，…………………………………………2分
，
． ………………………………………………………4分
经检验：是原方程的解．……………………………………………5分
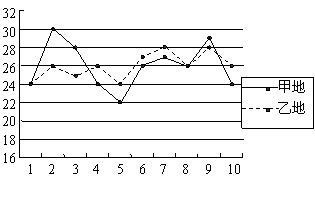
7.
（宣武一模）如图，是甲、乙两地5月下旬的日平均气温统计图，则甲、乙两地这10天日平均气温的方差大小关系为：
．
【答案】 >
⑵ 统计表和统计图
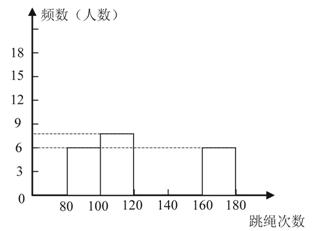
1. （大兴一模）为了进一步了解学生的身体素质情况体育老师对初三年级（1）班50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图．如下所示：
 |
| 组别 | 次数 | 频数（人数） |
| 第1组 |
|
|
| 第2组 |
|
|
| 第3组 |
|
|
| 第4组 |
|
|
| 第5组 |
|
|
第21题图
请结合图表完成下列问题：
（1）表中的
；
（2）请把频数分布直方图补充完整；
（3）这个样本数据的中位数落在第 组；
（4）若初三年级学生一分钟跳绳次数（
）达标要求是：
为不合格；
为合格；
为良；
为优．根据以上信息，请你给学校或初三年级同学提一条合理化建议：
．
【答案】（1）12；…………………………………………………………………………………1分
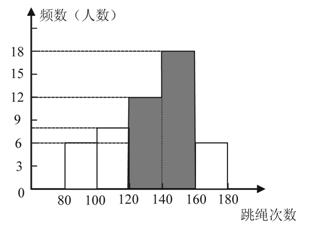
（2）画图答案如下图所示：………………………………………………………2分
（3）中位数落在第3组；………………………………………………………………3分
（4）只要是合理建议．………………………………………………………………4分
2.
(丰台一模)数学教师将相关教学方法作为调查内容发到全年级
名学生的手中，要求每位学生选出自己喜欢的一种，调查结果如下列统计图所示：
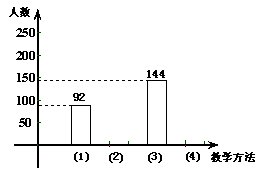
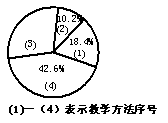
(1)请你将扇形统计图和条形统计图补充完整；
(2)写出学生喜欢的教学方法的众数；
(3)针对调查结果，请你发表不超过30字的简短评说。
【答案】
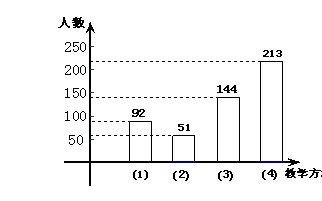
⑴
………………
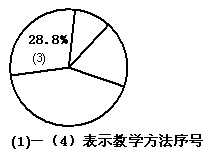
分
(名)
(名)
⑵ 学生喜欢第(4)种教学方法．众数是213．… …………………
分
⑶ 略．（合理合法即给分） ………………………………………
分
3. （宣武一模）“农民也可以报销医疗费了！”这是某市推行新型农村合作医疗的成果.村民只要每人每年交10元钱，就可以加入合作医疗，每年先由自己支付医疗费，年终时可以得到按一定比例返回的返回款.这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民，根据收集到的数据绘制了如下的统计图.
 |
根据以上信息，解答以下问题：
⑴ 本次调查了多少村民?被调查的村民中，有多少人参加合作医疗得到了返回款？
⑵ 该乡若有10000名村民，请你估计有多少人参加了合作医疗？要使两年后参加合作医疗的人数增加到9680人，假设这两年的年增长率相同，求这个年增长率.
【答案】⑴
240+60=300（人），240
%=6（人）； …………………………… 2分
⑵ 参加合作医疗的百分率为
%，
估计该乡参加合作医疗的村民有1000080%=8000（人）； …………………………… 3分
设年增长率为，由题意知
，
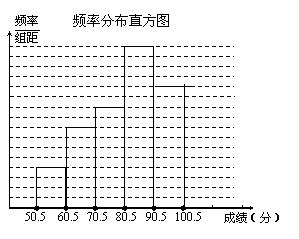
4. （石景山二模）为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成的频率分布表和频率分布直方图，解答下列问题：
⑴ 填充频率分布表中的空格；
⑵ 补全频率分布直方图；
⑶ 全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？（不要求说明理由）
答： ．
|
| 频率分布表 | ||
| 分组 | 频数 | 频率 |
| 50.5～60.5 | 4 | 0.08 |
| 60.5～70.5 | 8 | 0.16 |
| 70.5～80.5 | 10 | 0.20 |
| 80.5～90.5 | 16 | 0.32 |
| 90.5～100.5 | ||
| 合计 | ||
【答案】⑴ 答案如下表； ………………………2分
⑵ 答案如下图； ………………………4分
 |
| 频率分布表 | ||
| 分组 | 频数 | 频率 |
| 50.5～60.5 | 4 | 0.08 |
| 60.5～70.5 | 8 | 0.16 |
| 70.5～80.5 | 10 | 0.20 |
| 80.5～90.5 | 16 | 0.32 |
| 90.5～100.5 | 12 | 0.24 |
| 合计 | 50 | 1 |
⑶ 80.5～90.5. ………………………5分
二、概率
1. (丰台一模)在英语单词“Olympic Games”（奥运会）中任意选择一个字母，这个字母为“m”的
概率是 ．
【答案】
.
2. （大兴一模）如图，转动转盘，转盘停止转动时指针指向阴影部分的概率是
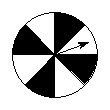【答案】
3. （海淀一模）一个口袋中有3个红球和6个黄球，这两种球除颜色外没有任何区别，随机的从口袋中任取出一个球，取到黄球的概率是 .
【答案】
.
4.
（朝阳一模）某校准备在八年级⑴班的
名团员中选
名作为“奥运志愿者”，其中团员晶晶被选中的概率为（ ）
【答案】
 |
5.
（宣武一模）如图，一个小球从
点沿制定的轨道下落，在每个交叉口都有向左或向右两种机会均等的结果，小球最终到达
点的概率是（ ）.
（A）
（B）
（C）
（D）
【答案】
6. （石景山二模） 从甲、乙、丙三人中选两名代表，甲被选中的概率为 （ ）
A．
B.
C.
D.1
【答案】 C
7. （昌平二模）下列事件中，是必然事件的是（ ）
Ａ．我市夏季的平均气温比冬季的平均气温高.
Ｂ．掷一枚均匀硬币，正面一定朝上.
Ｃ．打开电视机，正在播放动画片.
Ｄ．每周的星期日一定是晴天.
【答案】 A