九年级(下)二次函数单元检测题
一、选择题(每小题10分,共30分)
1、已知二次函数![]() 、
、![]() 、
、![]() ,它们的图像开口由小到大的顺序是( )
,它们的图像开口由小到大的顺序是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、抛物线![]() 的顶点坐标是( )
的顶点坐标是( )
A、(2,0) B、(-2,0) C、(0,2) D、(0,-2)
 3、二次函数
3、二次函数![]() 的图象沿
的图象沿![]() 轴向左平移2个单位,再沿
轴向左平移2个单位,再沿![]() 轴向上平移3个单位,得到的图象的函数解析式为
轴向上平移3个单位,得到的图象的函数解析式为![]() ,则b与c分别等于( )
,则b与c分别等于( )
A、6,4 B、-8,14 C、-6,6 D、-8,-14
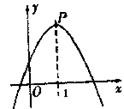
4、如图所示,抛物线顶点坐标是P(1,3),则函数y随自变量x的增大而减小
的x的取值范围是( )
A、x>3 B、x<3 C、x>1 D、x<1
5、二次函数![]() 的图象在
的图象在![]() 轴上截得的线段长为( )
轴上截得的线段长为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、抛物线![]() 与
与![]() 轴交点的个数为( )
轴交点的个数为( )
A、0 B、1 C、2 D、以上都不对
7、抛物线![]() ,对称轴为直线
,对称轴为直线![]() =2,且经过点P(3,0),则
=2,且经过点P(3,0),则![]() 的值为( )
的值为( )
A、-1 B、0 C、1 D、3
 8、若方程
8、若方程![]() 的两个根是-3和1,那么二次函数
的两个根是-3和1,那么二次函数![]() 的图象的对称轴是直线( )
的图象的对称轴是直线( )
A、![]() =-3 B、
=-3 B、![]() =-2 C、
=-2 C、![]() =-1 D、
=-1 D、![]() =1
=1
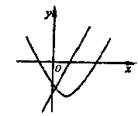
9、函数![]() 与
与![]() 的图象如图所示,
的图象如图所示,
则下列选项中正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
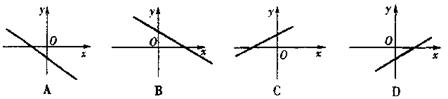
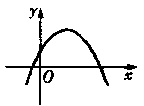 10、已知函数
10、已知函数![]() 的图象如图所示,则函数
的图象如图所示,则函数![]() 的图象是( )
的图象是( )
 |
二、填空题(每小题4分,共40分)
 1、若
1、若![]() 是二次函数,则
是二次函数,则![]() =______;
=______;
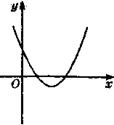
2、已知二次函数![]() 的图象如图所示,
的图象如图所示,
则a___0,b___0,c___0,![]() ____0;
____0;
3、抛物线![]() 的对称轴为直线_______,顶点坐标为______,与
的对称轴为直线_______,顶点坐标为______,与![]() 轴的交点坐标为________;
轴的交点坐标为________;
4、写出一个经过(0,-2)的抛物线的解析式_______________;
5、若二次函数![]() 的图象经过原点,则m=_________;
的图象经过原点,则m=_________;
6、抛物线![]() 与x轴交点的坐标为_________;
与x轴交点的坐标为_________;
7、函数![]() 有最____值,最值为_______;
有最____值,最值为_______;
8、已知函数![]() 的图象关于y轴对称,则m=________;
的图象关于y轴对称,则m=________;
9、关于x的一元二次方程![]() 没有实数根,则抛物线
没有实数根,则抛物线![]() 的顶点在第_____象限;
的顶点在第_____象限;
10、抛物线![]() 与x轴的正半轴交于点A、B两点,与y轴交于点C,且线段AB的长为1,△ABC的面积为1,则b的值为______。
与x轴的正半轴交于点A、B两点,与y轴交于点C,且线段AB的长为1,△ABC的面积为1,则b的值为______。
三、解答题:
1、根据条件求二次函数的解析式(每小题5分,共20分)
(1)抛物线过(-1,-22),(0,-8),(2,8)三点;
(2)抛物线过(-1,0),(3,0),(1,-5)三点;
(3)抛物线在x轴上截得的线段长为4,且顶点坐标是(3,-2);
(4)二次函数的图象经过点(-1,0),(3,0),且最大值是3。
2、(10分)已知抛物线过点A(-1,0),B(0,6),对称轴为直线x=1
(1)求抛物线的解析式
(2)画出抛物线的草图
(3)根据图象回答:当x取何值时,y>0
3、(10分)某旅社有客房120间,每间房间的日租金为50元,每天都客满,旅社装修后要提高租金,经市场调查,如果一间客房的日租金每增加5元,则每天出租的客房会减少6间。不考虑其他因素,旅社将每间客房的日租金提高到多少元时,客房日租金的总收入最高?比装修前的日租金总收入增加多少元?
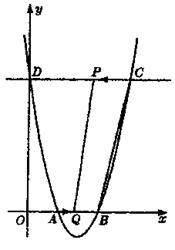
4、(10分)如图,二次函数![]() 的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
(1)求二次函数的解析式;
(2)设点A的坐标为(x,y),试求矩形ABCD的周长P关于自变量x的函数解析式,并求出自变量x的取值范围;
 (3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论。
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论。