初三三月份数学月考试卷

初三三月份数学月考试卷

出卷人：南昌十四中　余艳红

班级：　　　　  　　 姓名：　　　　 

一、我会选择（3分×10=30分）

⒈满足的整数的个数是（　　）

（A）5　（B）4　（C）3　（D）无数

⒉如图，量角器外缘上有A、B两点它们所表示的读数分别是80°、50°，则应为

（　　 ）.

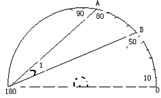（A）25° （B）15° （C）30°（D）50°

⒊根据图6中的信息，经过估算，下列数值与正方形网格中∠ɑ的正切值最接近

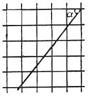的是（　　 ）.

（A）0.6246　　 （B）0.8121

（C）1.2252　　 （D）2.1809

⒋点A关于x轴的对称点为（2，－1），则点A的坐标为

　 （A）（－2，－1）　 （B）（2，1）　　 （C）（－2，1）　　（D）（2，－1）

⒌两圆的半径分别为3和4，圆心距为d，且这两圆没有公切线，则d的取值范围为 （A）d > 7　　 （B）1 < d <7　（C）3 < d <4　 （D）0 < d < 1

⒍使用直角钢尺检查某一工件是否恰好是半圆形的凹面，成半圆形的为合格，如图所示的四种情况中合格的是　　（　　）

⒎将一副直角三角板按图14叠放，则△AOB与△DOC的面积之比等于（　　　）.

（A）　　　　　 （B）　　　 （C）　　 　　　 （D）

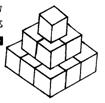
⒏一位美术老师在课堂上进行立体模型素描教学时，把14个棱长为 1分米的正方体摆在课桌上成如下右图形式，然后他把露出的表面都涂上不同的颜色，则被他涂上颜色部分的面积为（　　）

（A）33分米²（B）24分米²（C）21分米²（D）42分米²

⒐如下左图，弦CD经过AB的中点P，已知CP：DP=1：9，CD=10cm，则AB长为（）cm

A 3　　B 6　　C 9　　D　12

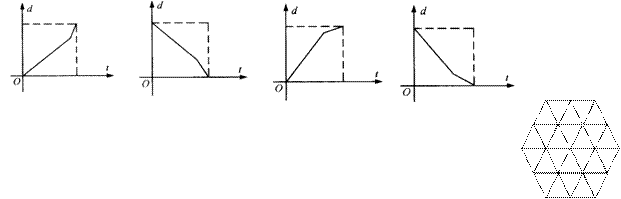
⒑某学生离家上学校，由于时间紧迫，一开始就跑步，待跑了足够长且累了则减速走完余下的路。若用纵轴表示离学校的距离d，横轴表示出发后的时间t，则较符合学生运动的（　　）

二、我会填空（3分×5=15分）

11、请在由边长为1的小正三角形组成的虚线网格中，画出一个所有顶点均在格点上，

且至少有一条边为无理数的等腰三角形．

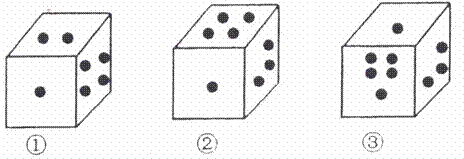
12、有一枚骰子，它的三种放法如下图所示，则这三种放法的底面上的点数之和是　　　　　  .

13、第一宇宙速度约为7919.米／秒，将它保留两个有效数字后的近似数是______________。

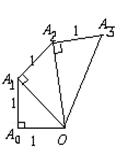14、11、已知A₀ A₁= A₁A₂₌ A₂A ₃OOA O，图中的螺旋形由一系列直角三角形组成，则第n个三角形的面积为　　　　 ，周长为　　　　　 .

15、在日常生活、生产和其他科学中存在大量的型的数量关系，例如：

利息=本金X利率　电压=电流强度X电阻

请写出一个除上面所举两例以外的实例：__________。

　　

友情提示：请将第一、二大题的答案写在下列答题卡内

题号

⒈

⒉

⒊

⒋

⒌

⒍

⒎

⒏

⒐

⒑

答案

题号

⒒

⒓

⒔

⒕

⒖

答案

三、我会计算：（6分×4=24分）

16、计算：

17解方程：3x²+5x-1=0

18一块如图所示的三角形地面，（1）用尺规作出AC边上的高（2）现准备种植每平方米售价10元的草皮以美化环境，则购买这种草皮至少需要多少元？

19、化简代数式，然后请你取一个你喜欢的x的值代入求　 值。

四、我会解答：（7分×3=21分）（第21题提供了二个题，请任选择一个作答，多作无效）

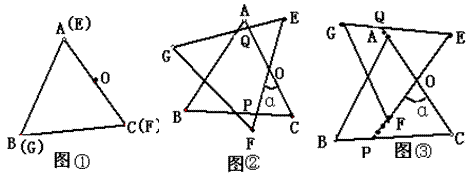
20、△ABC和△EFG是两块完全重合的等边三角形纸片,(如图①所示)O是AB(或EF)的中点,△ABC不动,将△EFG绕O点顺时针转α﹝0°＜α＜120°﹞角. (2007年江西课标样卷)

(1)　试分别说明α为多少度时,点F在△ABC外部、BC上、内部（不证明）？

（2）当点F不在BC上时，在图②、图③两种情况下（设EF或延长线与BC交于P，EG与CA或延长线交于Q，分别写出OP与OQ的数量关系，并将图③情况给予说明.

　

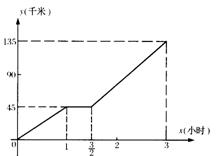21如图，坐标平面里的图像表示一汽车从甲地到乙地时间x与路程y之间的函数关系，横线表

示停车修理。（1）根据图像回答下列问题：

前1小时汽车的速度是多少千米／时；

停车修理的时间为多少？；后小时汽车的速度

是多少千米/时？甲、乙两地相距多少千米？

（2）适当选取图像中所给的数据，编一个一元一次

方程应用题，并列出方程（不要求解）

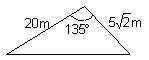
22、如图，海岛A四周20海里范围内是暗礁区，一艘货轮由东向西航行，在B处见岛A在北偏西60⁰，航行24海里后到C处，见岛A在北偏西30⁰，货轮继续向西航行，有无触礁危险？

五、我会应用：（10分×3=30分）

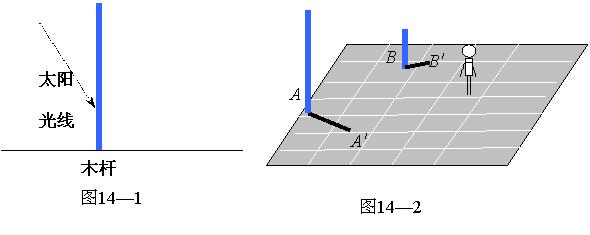
23、（1）一木杆按如图14—1所示的方式直立在地面上，请在图中画出它在阳光下的影子（用线段CD表示）；（2）图14—2是两根标杆及它们在灯光下的影子．请在图中画出光源的位置（用点P表示）；并在图如图，在直角坐标系中，以点P（2，1）为圆心，R为半径画圆．

（1）在画⊙P时，由于R的取值不同，⊙P与坐标系的公共点的个数就不同，请将你对这个问题的探究结果填入下表：

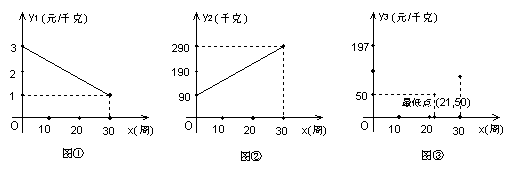
24、某水产基地种植某种食用海藻，从三月一日起的30周内，它的市场价格与上市时间的关系用图①线段表示；它的平均亩产量与时间的关系用图②线段表示；它的每亩平均成本与上市时间的关系用图③抛物线表示。（1）写出图①、图②、所表示的函数关系式；

　（2）若市场价×亩产量－亩平均成本 = 每亩总利润，问哪一周上市的海藻利润最大？最大利润是多少？

25、已知二次函数的图像过点A（2，0）．且与直线相交于B、 C两点，点B在x轴上，点C在y轴上。（1）求二次函数的解析式。

（2）如果P（x，y）是线段BC上的动点，O为坐标原点，试求S△POA的面积S与x之间的函数关系式，并求出自变量的取值范围。

（3）是否存在这样的点使PO=AO？若存在，求出P点的坐标；若不存在，请说明理由。