九年级数学上学期期末考试题
数 学 试 卷
班级 姓名 座号
一、选择题：本大题共6小题，每小题4分，共24分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．
1．一个数9的平方根是--------（ ）
A. 
B．3 C．±3 D．81
2．计算
的结果是--------------------（ ）
A.
B.
C.
D. 
3．下列图形中，是中心对称图形的是-----------------（ ）
A.菱形 B.等腰梯形 C.等边三角形 D.等腰直角三角形
4．一个钢球沿坡角
的斜坡向上滚动了
米，此时钢球距地面的高度是（ ）米
Ａ．
Ｂ．
Ｃ．
Ｄ．
5．一个三角形的两边长为3和6，第三边的边长是方程
的根，则这个三角形的周长是-------------------------------------------（ ）
Ａ.11 Ｂ.11或13 Ｃ.11和13 Ｄ.13
6．如图是每个面上都标有一个汉字的正方体的平面展开图，在此正方体上与“我”字相对的面上的汉字是（ ）
A．“城” B．“东” C．“中” D．“学”
二、填空题：本大题共12小题，每小题3分，共36分
7．当x＝
时，分式
无意义.
8．一元二次方程
的解是______________．
9．分解因式：
．
10．城东菜市场某水果店1至6月份的销售情况（单位：千克）为450、440、420、480、580、550，则这组数据的极差是 千克
11．投掷一枚普通的正方体骰子，则P（掷出的数字为偶数）＝ ．
12．若
，则
．
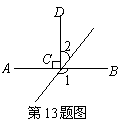
13．如图，
，垂足为
，则
度．
14．如图，□ABCD的周长为20，对角线
的长为5，则
的周长为 ．
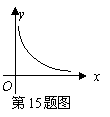
15．反比例函数
图象如图所示，则
随
的增大而
．
 | |||
 | |||
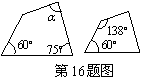
16．若如图所示的两个四边形相似，则
的度数是
17．若一元二次方程
有一根是
，则
．
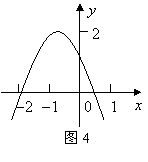18．如图4所示，二次函数
的图象经过点
，且与轴交点的横坐标分别为
，其中
，
，下列结论：
①
；
②
；
③
；
④
．
其中正确的个数有
提示：抛物线的对称轴是
，顶点坐标是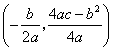
三、解答题（共90分）
19．计算（本题满分8分）
20．（8分）先化简下面的代数式，再求值：
，其中
21．用适当方法解下列方程：（每小题4分，共8分）
（1）
（2）
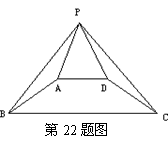
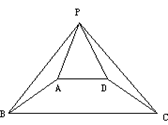
22．（8分）如图，已知四边形ABCD是等腰梯形，AB=CD，AD∥BC，PB=PC。求证：PA=PD。
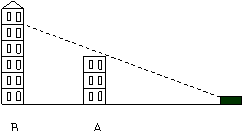23．（8分）小明开着汽车在平坦的公路上行驶,前放出现两座建筑物A、B(如图),在(1)处小颖能看到B建筑物的一部分,(如图),此时,小明的视角为30°,已知A建筑物高25米.
(1)请问汽车行驶到什么位置时,小明刚好看不到建筑物B?请在图中标出这个点.
(2)若小明刚好看不到B建筑物时,他的视线与公路的夹角为40°,请问他向前行驶了多少米?( 精确到0.1)
24．（本题满分8分）小辰家买了一辆小轿车，小辰连续记录了七天中每天行驶的路程：
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 路程（千米） | 36 | 29 | 27 | 40 | 43 | 72 | 33 |
请你用学过的统计知识解决下面的问题：
（1）小辰家的轿车每月（按30天计算）要行驶多少千米？
（2）若每行驶100千米需汽油8升，汽油每升
元，请你算出小辰家一年（按12个月计算）的汽油费用大约是多少元（精确到百元）．
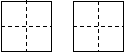
25．（8分）汉字是世界上最古老的文字之一，字形结构体现人类追求均衡对称、和谐稳定的天性．如图，三个汉字可以看成是轴对称图形．
（1）请在方框中再写出2个类似轴对称图形的汉字；
（2）小敏和小慧利用“土”、“口”、“木”三个汉字设计一个游戏，规则如下：将这三个汉字分别写在背面都相同的三张卡片上，背面朝上洗匀后抽出一张，放回洗匀后再抽出一张，若两次抽出的汉字能构成上下结构的汉字（如“土”“土”构成“圭”）小敏获胜，否则小慧获胜．你认为这个游戏对谁有利？请用列表或画树状图的方法进行分析并写出构成的汉字进行说明．
 |
解：（1）
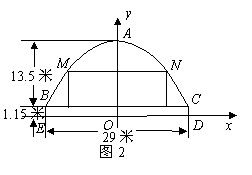
26．（8分）（13分））明珠大剧场座落在聊城东昌湖西岸，其上部为能够旋转的拱形钢结构，并且具有开启、闭合功能，全国独一无二，如图1．舞台顶部横剖面拱形可近似看作抛物线的一部分，其中舞台高度
米，台口高度
米，台口宽度
米，如图2．以
所在直线为轴，过拱顶
点且垂直于的直线为轴，建立平面直角坐标系．
（1）求拱形抛物线的函数关系式；
（2）舞台大幕悬挂在长度为
米的横梁
上，其下沿恰与舞台面接触，求大幕的高度（精确到
米）．
27．（13分）为了鼓励节能降耗，某市规定如下用电收费标准：每户每月的用电量不超过120度时，电价为a元/度；超过120度时，不超过部分仍为a元/度，超过部分为b元/度．已知某用户五月份用电115度，交电费69元，六月份用电140度，交电费94元．
（1）求a，b的值；（4分）
（2）设该用户每月用电量为x（度），应付电费为y（元）．
①分别求出
和＞120时，y与x之间的函数关系式；
②若该用户计划七月份所付电费不超过83元，问该用户七月份最多可用电多少度？
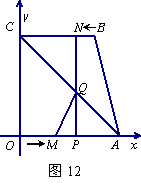
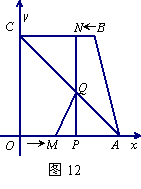28．（13分）如图12， 四边形OABC为直角梯形，A（4，0），B（3，4），C（0，4）． 点
从
出发以每秒2个单位长度的速度向运动；点
从
同时出发，以每秒1个单位长度的速度向
运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点作
垂直轴于点
，连结AC交NP于Q，连结MQ．
（1）点 （填M或N）能到达终点；
（2）求△AQM的面积S与运动时间t的函数关系式，
并写出自变量t的取值范围，当t为何值时，S的值最大；
（3）是否存在点M，使得△AQM为直角三角形？若存在，
求出点M的坐标，若不存在，说明理由．
 | |||
| |||
泉州市城东中学2008级九年级上学期期末考
数 学 答 题 卷
友情提示：请在方框里面作答，超出方框均不算分。
一、选择题：本大题共6小题，每小题4分，共24分．
1． 2. 3. 4. 5. 6.
二、填空题：本大题共12小题，每小题3分，共36分
7． 8. 9. 10. 11. 12.
13． 14. 15. 16. 17. 18.
三、解答题（共90分）
19．
解：原式＝
20．先化简再求值，其中
解：原式＝
21．（1）
（2）
22．证明：
23．解：
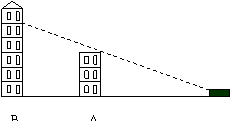
24．解：
⑴ ⑵
25．解：（1）
|
（2）
26．解：⑴
⑵
 |
27．解：（1）
(2) ①
②
28．解：（1）点 （填M或N）能到达终点
（2）