二次函数 应用问题
二次函数在各方面的应用比较广泛，本节中通过几个例题及几个练习题，举例说明它在一些问题中的应用.
例1 某商场以每件42元的价钱购进一种服装，根据试销得知：这种服装每天的销售量
（件），与每件的销售价
（元/件）可看成是一次函数关系：
1.
写出商场卖这种服装每天的销售利润
与每件的销售价之间的函数关系式（每天的销售利润是指所卖出服装的销售价与购进价的差）；
2. 通过对所得函数关系式进行配方，指出：商场要想每天获得最大的销售利润，每件的销售价定为多少最为合适；最大销售利润为多少？
分析：商场的利润是由每件商品的利润乘每天的销售的数量所决定。
在这个问题中，每件服装的利润为（
），而销售的件数是（
+204），那么就能得到一个与之间的函数关系，这个函数是二次函数.
要求销售的最大利润，就是要求这个二次函数的最大值.
解：（1）由题意，销售利润与每件的销售价之间的函数关系为
=（－42）（－3＋204），即=－32+
8568
（2）配方，得=－3（－55）2+507
∴当每件的销售价为55元时，可取得最大利润，每天最大销售利润为507元.
例2 某跳水运动员进行10米跳台跳水训练时，身体（看成一点）在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线（图中标出的数据为已知条件）.
在跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面
米，入水处距池边的距离为4米，运动员在距水面高度为5米以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误.
（1）求这条抛物线的解析式；
（2）在某次试跳中，测得运动员在
空中的运动路线是（1）中的抛物线，
且运动员在空中调整好入水姿势时，距
池边的水平距离为
米，问此次跳水会不会失误？
并通过计算说明理由.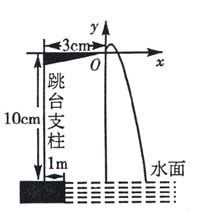 
分析：（1）在给出的直角坐标系中，要确定抛物线的解析式，就要确定抛物线上三个点的坐标，如起跳点O（0，0），入水点（2，－10），最高点的纵点标为
.
（2）求出抛物线的解析式后，要判断此次跳水会不会失误，就是要看当该运动员在距池边水平距离为米.，
时，该运动员是不是距水面高度为5米.
解：（1）在给定的直角坐标系下，设最高点为A，入水点为B，抛物线的解析式为
.
由题意，知O（0，0），B（2，－10），且顶点A的纵坐标为.
解得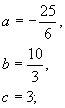 
或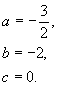 
∵抛物线对称轴在轴右侧，∴
又∵抛物线开口向下，∴
.
∴抛物线的解析式为
（2）当运动员在空中距池边的水平距离为米时，
即时，
∴此时运动员距水面的高为
因此，此次跳水会失误.
本节练习题如下：
1、某商场以每件30元的价格购进一种商品，试销中发现，这种商品每天的销量
（件）与每件的销售价（元）满足一次函数：
（1）写出商场卖这种商品每天的销售利润与每件的销售价间的函数数关系式.
（2）如果商场要想每天获得最大的销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？
2、如图，一边靠学校院墙，其它三边用40米长的篱笆围成一个矩形花圃，设矩形
的边
米，面积为
平方米.
（1）求：与之间的函数关系式，并求当
米2时，的值；
（2）设矩形的边
米，如果
满足关系式
即矩形成黄金矩形，求此黄金矩形的长和宽.
.
练习1答案：
当定价为42元时，最大销售利润为432元.
练习2答案：（1）
当时，
（2）当
则
①
又
②
由①、②解得
，
其中20
不合题意，舍去，
当矩形成黄金矩形时，宽为
，长为
.
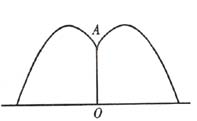
3、某地要建造一个圆形喷水池，在水池中央垂直于水面安装一个花形柱子OA，O恰在水面中心，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过OA的任一平面上，抛物线形状如图所示，如图建立直角坐标系，水流喷出的高度
与水平距离
之间的关系式是
. 
请回答下列问题：
1. 柱子OA的高度为多少米？
2. 喷出的水流距水平面的最大高度是多少米？
若不计其它因素，水池的半径至少要多少米，才能喷出的水流不至于落在池外？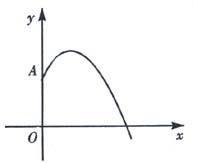 
练习3答案：
（1）OA高度为
米.
（2）当
时，
，即水流距水平面的最大高为
米.
（3）当
时，
其中
不合题意，
答：水池的半径至少要2.5米，才能使喷出的水流不至于落在池外.
二次函数的图象是一条抛物线，抛物线又是一种常见的图形，在实际生活中用处广泛，因此结合实际问题学习抛物线的有关性质，可以更加深刻地认识事物的本质.
1.
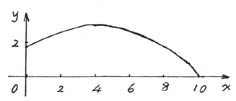
一男生掷铅球，铅球行进高度(m)，与水平距离
(m)之间的关系是 
1. 在直角坐标系画出函数图象，并求出铅球掷出的距离；
2. 在体育加试中，男生铅球的优秀成绩为11m，若上述抛物线顶点不变，开口方向不变，试计算成绩优秀时，铅球出手的最低高度是多少？
分析：求铅球掷出的距离，就是求
时，的值是多少.
当铅球掷出的距离为11m时，抛物线过点（11，0），并且抛物线的顶点不变，那么求出这条抛物线的解析式，并且求出出手高度（抛物线与轴交点）.
解：（1）当时， 
，解得 
.
不合题意，舍去. 铅球推出的距离为10米.
（2）抛物线配方成
, 顶点坐标为（4，3）
如果抛物线过（11，0），顶点为（4，3），设抛物线为
， 
， 
.
.
因此出手高度最低为
米.
例2 某公园草坪的护栏是由50段形状相同的抛物线形组成的、为牢固起见，每段护拦需按间距0.4m加设不锈钢管（如图）作成的立柱，为了计算所需不锈钢管立柱的总长度，设计人员利用如图所示的直角坐标计算.
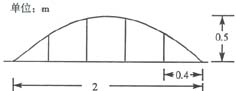
1. 求该抛物线的解析式；
2. 计算所需不锈钢管立柱的总长度.
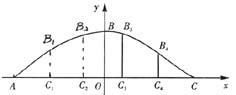
分析：为了求出抛物线的解析式，把抛物线放在直角坐标系中，根据题意可知道，
C（1，0），A（－1，0），B（0，0.5），且B为抛物线的顶点，从而可以求出抛物线的解析式.
要求不锈钢立柱的总长度，就要求出B1、B2、B3、B4的纵坐标，而B3与C3的横坐标为0.2，则可求出B3的纵坐标，同理，C4的横坐标为0.6，从而可求出所有立柱的长及所需钢管的总长度.
解：（1）在直角坐标系中，设函数解析式为
，B点坐标为（0，0.5），C点坐标为（1，0）
抛物线的解析式为
（2）分别过AC的五等分点C1、C2、C3、C4作轴的垂线，交抛物线于B1
B2、B3、B4点，则C1 B1、C2 B2、C3 B3、C4 B4的长就是一段护栏内的四条立柱的长，点C3、C4的坐标为（0.2，0）（0.6，0），则B3、B4的横坐标分别为
把
分别代入,
得
. 由对称性可求得B1、B2的纵坐标.
所以四条立柱的长为
C1 B1＝C4 B4＝0.32（m）, C2 B2=C3 B3=0.48(m).
所需不锈钢立柱的总长为
答：所需不锈钢立柱的总为长80m.
为了更好的巩固与二次函数知识应用问题有关的知识，下面的练习同学们可自己完成.
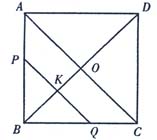1、已知：如图正方形ABCD的边长为
，在对角线BD上有一动点K，过K作PQ∥AC并交正方形的两边为P、Q，设BK＝，
＝.
求：（1）关于的函数关系式；
（2）画出函数图像。
练习1答案
（1）设AC与BD相交于O，当K在OB上时，
∵O为AD中点， K为PQ中点， ∴PQ＝2BK＝2
∵
（0<
<1）
当K在OD上运动时，KD＝2－， ∴PQ＝2（2－）,
（1≤＜2）
∴所求的函数关系式为
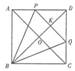
（2）函数图象如图所示。
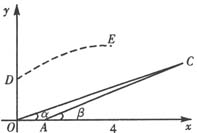2、如图，这是某空防部队进行射击训练时在平面直角坐标系中的示意图，在地面O、A两个观测点测得空中固定目标C的仰角分别为
，OA＝1千米， 
，位于O点正上方
千米D点处的直升飞机向目标C发射防空导弹，该导弹运动达到距地面最大高度3千米时，相应的水平距离为4千米（即图中E点）。
（1）若导弹运行轨道为一抛物线，
求该抛物线的解析式；
（2）说明按（1）中轨道运动的导
弹能否击中目标C的理由。
练习题2答案
（1）D（0，），E是抛物线的顶点，坐标为（4，3）
设抛物线的解析式 
（2）设C点坐标为
，则
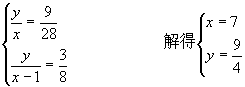
把
代入抛物线解析式，得
∴C在抛物线上，即导弹能击中目标。
3、如图，这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图，横断面的地平线为轴，横断面的对称轴为轴，桥拱的
部分为一段抛物线，顶点G的高度为8米，AD和
是两侧高为5.5米的支柱，OA和
为两个方向的汽车通行区，宽都为15米，线段CD和
为两段对称的上桥斜坡，其坡度为1：4
（1）求桥拱所在抛物
线的解析式
的长；
（2）BE和
为支撑斜坡的
立柱，其高都为4米，相应
的AB和
为两个方向的行
人及非机动车通行区，求AB和的宽.
（3）按规定，汽车通过该桥下时，载货最高处和桥拱之间的距离不得小于0.4米，今有一大型货汽车，装载某大型设备后，其宽为4米，车载大型设备的顶部与地面的距离均为7米，它能否从OA（或）区域安通过？请说明理由.
练习3答案
（1）设DG
所在的抛物线的解析式为
由题意得G（0，8），D（15，5.5）
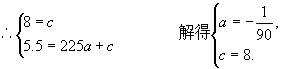
∴DGDˊ所在的抛物线的解析式为
.
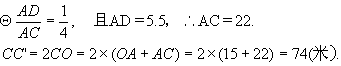
（2）
.
（米）.
答：AB和的宽都是6米.
（3）该大型货车可以从OA（或）区域安全通过
在中，当
时，
，
∴该大型货车可以从OA（或）区域安全通过.