2008年函数及其图象总复习教材教法分析
海淀区教师进修学校 方 菁
一、中考要求：见中考说明
| 基本要求 | 略高要求 | 较高要求 | |
| 平 面直 角坐 标系 | 会建立直角坐标系（包括在方格纸上）描述物体的位置； 在给定的直角坐标系中，会确定坐标与点之间的对应关系； 了解特殊位置点的坐标特征 | 由点的特殊位置，会求相关字母的范围； 已知点坐标，会求出点到轴的距离 | 在同一直角坐标系中，感受图形变换后点的坐标变化，会用点的坐标刻画点的移动； 能灵活运用不同的方式确定物体的位置 |
| 函 数及 其图 象 | 探索具体问题中的数量关系，了解常量和变量的意义； 结合实际问题了解函数的概念和三种表示方法； 会确定简单的函数（整式、分式和实际问题）中的自变量取值范围，并会求函数值； 会用描点法画出简单函数的图像 | 探索具体问题中的数量关系和变化规律，会用适当的方法刻画某些实际问题中变量之间的关系； 结合函数关系的分析，能对变量的变化趋势进行初步预测； 能结合图象对简单实际问题中函数关系进行分析 | |
| 一 次函 数 | 能结合具体问题探索一次函数的意义，会求它的表达式； 会画图象 | 会用性质解决“数”、“形”结合问题； 根据一次函数的解析式，会求其图象与坐标轴的交点坐标 | 能根据图象与解析式之间的对应关系，解决相关问题； 会解决与一次函数有关的实际问题 |
| 反 比例 函数 | 能结合具体情景探索反比例函数的意义，会求解析式，会画图象 | 会用反比例函数的性质；能用反比例函数的知识解 决相应的问题 | 能根据实际问题或图象解决反比例函数的问题 |
| 二 次函 数 | 能结合实际问题情景确定二次函数的表达式； 会用描点法画二次函数的图象 | 能从图象上认识二次函数的性质； 会根据公式确定图象的顶点、开口方向和对称轴； 会用二次函数的图象求一元二次方程的近似解 | 能解决简单的实际问题； 能解决与其他函数结合的实际问题 |
二、学习的章节
第17章 函数及其图象，第26章 二次函数
三、复习的依据
以《课程标准》为纲，华东师范大学教材、海淀区中考说明为本，海淀教师进修复习指导为依据，抓好三基（基础知识、基本技能、基本能力）、重点内容的落实.
注意《课程标准》与《教学大纲》的相同要求与不同点
降低要求之处：
1. 对《距离》只要求点到坐标轴的距离及同一坐标轴上两点间的距离公式(不能转化为一元二次方程根系关系)，不在同一数轴上两点间的距离公式不要求, (可用勾股定理转化为几何问题).
2. 二次函数交点式不要求.
3. 用待定系数法求函数解析式时，回避三元一次方程组，二元二次方程组，回避一元二次方程根与系数的关系.
提高要求之处：
1. 移动. 例9，例10，例18，例42，例43，例44
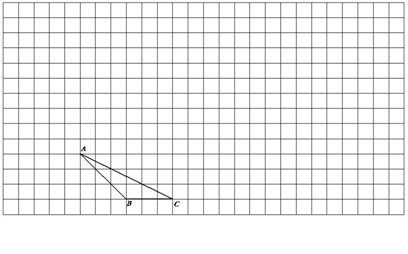
【图形的移动转化为点的移动】
例10 ★★ (海口市课改实验区2007) (1)请在如图所示的方格纸中，将△ABC向上平移3格，再向右平移6格，得△
，再将△绕点
按顺时针方向旋转
，得
△
，最后将△以点
为位似中心放大到2倍，得△
；
(2)请在方格纸的适当位置画上坐标轴(一个小正方形的边长为1个单位长度)，在你所建立的直角坐标系中，点C、
、的坐标分别为：点C(_____)、点 (_____)、
点 (_____)．
2. 估算 利用函数图象交点求近似值，预测. 例17，例32（2）
例17 新课程标准P36 例11
填表并观察下列两个函数的变化情况：
| X | 1 | 2 | 3 | 4 | 5 | … |
| Y1 = 50 + 2x | ||||||
| Y2 = 5x |
（1） 在同一个直角坐标系中画出上面两个函数的图象，比较它们有什么不同；
（2） 当 x 从1开始增大时，预测哪一个函数的值先到达100.
3. 直角坐标系 坐标轴的选取，图形变换. 例10
4. 应用. 多道例题
5. 直线与几何的结合（比例、勾股、面积等等）.
例25，例31，例44，例47，例49，例50，例51，例52 等等
6. 解题方法成为重点 多道例题
四、教材教法分析
（一）对直角坐标系的理解【数形结合】
【知识要点】
1. 特殊位置的点的坐标特点
各象限内的点, 坐标轴上的点 例1，例2，例3，例4
【点所在区域决定点坐标的正、负、零, 点到轴的距离决定点坐标的绝对值】
公式: 点到 x 轴的距离 = y
点到 y 轴的距离 = x
(垂线段的长) = （点坐标的绝对值）
几何（线段） 函数（坐标）
【转化为线段长用几何知识；转化为点的坐标用函数知识】 例25
象限角平分线上的点【利用坐标间的数量关系构造方程】 例5，例7（2）
第1、3象限角平分线上的点（ x、y ） x = y
第2、4象限角平分线上的点（ x、y ） x = - y
2. 两个具有特殊位置的点的坐标间的数量关系 例6
（1）对称性 （2）平行
【利用坐标间的数量关系构造方程】
【基本题型，基本方法】
1. 已知点的坐标 ★ 会求点到坐标轴的距离,
会求同一坐标轴上两点间的距离.
会求两坐标轴上两点间的距离, 会求点到原点的距离，会求仅有一点在坐标轴上的两点间的距离 （用勾股定理）
★ 由已知点的坐标求有关对称点的坐标 例6
★ 求图形变换后点的坐标，会用点的坐标刻化点的移动. 例10
2. 画点的坐标：（略)
3. 求点的坐标：
（1）定域定量法： 例7（1）
（2）构造方程法： 例5，例7（2）
（3）图象交点法：
（4） 观察图象法（含估算）
1）观察点的坐标： 例16，例28（2），例38等等
2）观察已知点有关对称点的坐标： 例6
3）观察函数图象与坐标轴交点的坐标：例16（1），例38，例39
4）观察两个函数图象交点的坐标： 例32（2）
5）观察点的坐标，求函数解析式： 例28（2）
（二）对函数有关概念的理解
【知识要点】
1. 函数定义 2. 函数的图象
【基本题型，基本方法】
1. 函数自变量取值范围
（1）解析式（使解析式有意义） 例11，
（2）图象（图象端点向 x 轴引垂线，由垂足对应的数看 x 的取值范围）例16（1）
★★（3）列表（表中自变量取值）
★★（4）应用（使实际问题有意义）
2. 函数值（实质是求代数式的值）： 例12（1）
3. 已知函数值，求自变量取值（实质是解方程）： 例12（2）
4. 会画函数图象： 例17
会画直角坐标系（三要素：方向、原点、单位长度）
会画函数图象：
一列表（不能取到的值加括号） 二描点（注意实心点与空心点）
三连线 （注意直线、射线、线段的区别；曲线、曲线段的区别）
四标解析式 （含自变量取值范围）
5. 会求函数图象上的特殊点的坐标：（并到三类函数）
（1）求与 y 轴的交点坐标， ( 0, c ) （看出来的）
（2）求与 x 轴的交点坐标， （算出来的）
1） ( x1,0 ),( x2,0 ) 令 y = 0 解方程解出来的，（Δ ≥ 0）
2） 已知( x1,0 )及对称轴，由对称性得( x2,0 ) （推出来的）
（三）对三类函数的理解（数形结合）
【知识要点】
| 函数 | 一次函数 | 反比例函数 | 二次函数 | |
|
解析式 | y = kx + b (k ≠o) |
(k ≠o) | y = ax2 + bx+c ( a ≠ 0 ) | |
|
结构 | 结构
| 结构
| 结构
| 结构
|
|
| 不平行于坐标轴的直线
| 加条件
| 对称轴平行y轴
| |
|
系数
|
定 向 |
|
|
|
| 定 轴 | —— | —— | ab符号 | |
|
定 点 （1）与y 轴的交点(交点恰在 y 轴上)
（2）抛物线 的顶点 | b 定点
常数项= 与y轴交点纵坐标 (常数项1 = 常数项2)
|
——
| c 定点
常数项= 与y轴交点纵坐标 ( 常数项1 = 常数项2 ) | |
| a、b、c
（- | ||||
|
定增减性 | k ＞ 0,y 随 x 增大而增大 k ＜ 0,y 随 x 增大而减小 | k ＞ 0,y 随 x 增大而减小 k ＜ 0,y 随 x 增大而增大 |
略 | |
|
| 定 点
| 令y = 0的根x
（x ，0） |
—— | 令y = 0的两根x1,x2 定点 （x1，0），（x2，0） |
形状
直线 
双曲线 
形状 加条件 结构
结构 
结构
结构
k 定向
k 定位置
a符号 开口方向
(0, b)
(0, c)
定点
，
）
令y = 0的根x
与x 轴的交点
定点
一次函数
【基本题型，基本方法】
1. 一次函数的解析式与它图象上的点【用方程思想】
1）求函数解析式 例15（1）（3）（4）（6）
【将点的坐标代入解析式，是构造关于“系数”方程的主要方法】
【转化点的坐标是求函数解析式的重要方法】
求函数解析式的步骤：
一设 （优选函数解析式，尽量用概念定系数，使待定的系数越少越好）
二构 （将点的坐标代入解析式，构造待定系数的方程或方程组，）
（用已知等量关系或几何条件，构造待定系数的方程或方程组）
三解 （解方程或方程组）
四回代（将解出来的系数代入所设的函数解析式）
例15（3） 若一次函数图象过A (2, -1)和B两点，其中点B是另一条直线y =﹣
x + 3与y 轴的交点，求这个一次函数的解析式. （定b待k）
2）求点的坐标 例15（2）（4）（5）（6）（7）
例15（7） 已知 y = 3x – 2 的图象经过点（ a，b ），且 a + b = 6，求a、b的值.
2. 一次函数中的数形结合【用数形结合的思想】（依形判数，由数思形）
看一次函数的图象
一看与 y 轴交点 ( 0, b )， 定常数项 b。 例16（1）
二看图象的走向定 k的符号：左低右高 k ＞ 0
左高右低 k ＜ 0 同步练习册 八册下 P17.3
三看图象的走向定函数的增减性： 例16（2）
左低右高 y 随 x 增大而增大,
左高右低 y 随 x 增大而减小
四看图象所在象限定k, b 符号：（略） 同步练习册 八册下 P17.1（2）
画一次函数的图象
例17 新课程标准P36 例11
填表并观察下列两个函数的变化情况：
| x | 1 | 2 | 3 | 4 | 5 | … |
| Y1 = 50 + 2x | ||||||
| Y2 = 5x |
（3） 在同一个直角坐标系中画出上面两个函数的图象，比较它们有什么不同；
（4） 当 x 从1开始增大时，预测哪一个函数的值先到达100.
3．图形的移动（翻转，平移，旋转）
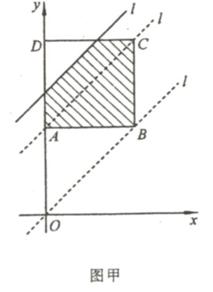
例19 （河南省2007）如图甲，边长为2的正方形ABCD中，顶点A的坐标是(0，2)．一次函数y = x + t的图像l随t的不同取值变化时，位于l的右下方由l和正方形的边围成的图像面积为S（阴影部分）
（1） 当t取何值时，S=3
（2） 在平面直角坐标系下（如图乙），画出S与t的图像。
 |
4. 与一次函数有关的实际问题 例20——例24
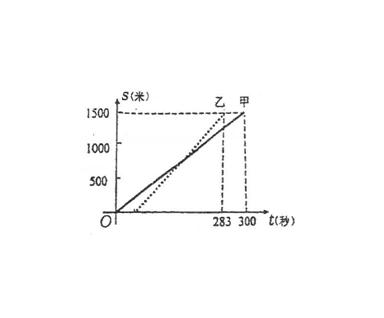
例21 甲、乙两人在一次赛跑中，路程s与时间t的关系如图所示（实线为甲的路程与时间的关系图像，虚线为乙），小王根据图像得到如下四个信息，其中错误的是： （ ）
(A) 这是一次1500米的赛跑
(B) 甲、乙两人中先到达终点的是乙
(C) 甲、乙同时起跑
(D) 甲在这次赛跑中的速度为5m/s
反比例函数
【基本题型，基本方法】
1. 反比例函数的解析式与它的图象上的点 例26，例27
例27 （1）（安徽省2007年） 近视眼镜的度数 y（度）与镜片焦距 x（米）成反比例. 已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数 y 与镜片焦距 x 之间的函数关系式是
. （优选y = 
）
（2） 已知 y = ( 2 - m )x m - 4是反比例函数，则 m = , 此函数图象在
第 象限. （优选y = kx - 1 ）
（3）（北京市海淀区2007年）已知反比例函数 
的图象经过
点（1，2），则函数 y = - kx 可确定为（ ）. （ 优选k = xy ）
（A）y = - 2x
（B）
y = 
（C）
（D）y = 2x
2. 反比例函数中的数形结合（依形判数、由数思形）
看反比例函数图象： 例28——例30
一看图象的位置定 k的符号：
一、三象限 k ＞ 0
二、四象限 k ＜ 0
二看图象的位置定函数的增减性：
一、三象限的每个象限内， y 随 x 增大而减小
二、四象限的每个象限内， y 随 x 增大而增大
例30（2）（山东省潍坊课改实验区2007）若M（
，y1）、N（
，y2）、P（
，y3）三点都在函数y=（k < 0）的图像上，则y1
、y2 、y3 的大小关系为 （ ）
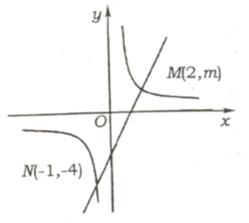（A）y2 >y3 >y1
（B）y2 >y1 >y3
（C）y3 >y1 >y2 （D）y3 >y2 >y1
3. 反比例函数的应用 例31
4. 相关的综合题 例32
例32 （2）（贵阳市课改实验区）如图，一次函数y= ax + b的图像与反比例函数y=的图象交于M、N两点
1）求反比例函数和一次函数的解析式；
2）根据图象写出使反比例函数的值大于一次函数的值的x的取值范围。
二次函数
【基本题型，基本方法】
1. 二次函数解析式与它图象上的点【用方程思想】 例33——例36
二次函数解析式的两种形式（注意隐含条件、优选解析式）：
y = ax2 + bx + c ( a ≠ 0 )
y = a(x – h)2 + k ( a ≠ 0 ) （已知对称轴、顶点）
例33 （4） 抛物线 y = 2x2 + bx – 5 过点A ( - 2, yA )，则 yA =
（6） 二次函数 y = ax2 + bx + c的图象与 x 轴交于点A ( - 3, 0 )，
对称轴x = -1，顶点C到x轴的距离为2，则设 y = ,
得方程为 ，解得 ，
此函数解析式为 . （优选顶点式）
2. 二次函数中的数形结合【用数形结合思想】（依形判数，由数思形）
看二次函数的图象：
一看与 y 轴交点 ( 0, c )， 定常数项 c. 例38
二看图象的开口方向定 a 的符号： 例37（1）（2）
开口向上 a ＞ 0
开口向下 a ＜ 0
三看抛物线与 x 轴的相对位置： 例37（4） 例41
抛物线与 x 轴有两个交点，⊿ ＞ 0；
抛物线与 x 轴有一个交点，⊿ ＝ 0；
抛物线与 x 轴无交点， ⊿ ＜ 0.
四看抛物线对称轴与 y 轴的相对位置： 例40（1）
对称轴在 y 轴的左侧，a 、b 同号：
对称轴在 y 轴的右侧，a 、b 异号.
五看图象的走向定函数的增减性：（以对称轴为界）
左低右高 y 随 x 增大而增大,
左高右低 y 随 x 增大而减小
六看部分图象对应的取值范围： 例37（3）
（图象端点向 x 轴引垂线，由垂足对应的数看 x 的取值范围）
（图象端点向 y 轴引垂线，由垂足对应的数看 y 的取值范围）
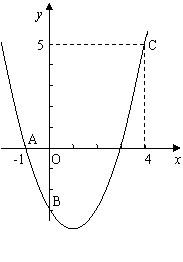例38（沈阳市2007）如图，二次函数y=ax2+bx+c的图象经过A、B、C三点.
（1）观察图象写出A、B、C三点的坐标，并求出此二次函数的解析式；
（2）求出此抛物线的顶点坐标和对称轴。
画二次函数图象 （略）
3．图形的移动（翻转，平移，旋转） 例42——例44
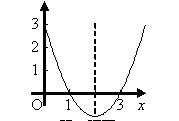
例42（1）（山东省潍坊课改实验区2007）抛物线y=ax2+bx+c如图所示，则它关
于y轴对称的抛物线的解析式为 。
4.
二次函数的应用
例45，例46
例45 （吉林省2007）如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距.某项研究表明，一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据：
| 指距d（cm） | 20 | 21 | 22 | 23 |
| 身高h（cm） | 160 | 169 | 178 | 187 |
（1） 求出h与d之间的函数关系式（不要求写出自变量d的取值范围）：
（2） 某人身高为196cm，一般情况下他的指距应是多少？
5. 相关的综合题 例47——例52
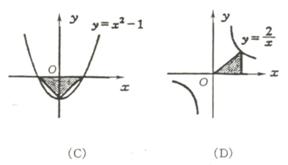
例51下列图中阴影部分的面积与算式
+（）2
+ 2-1的结果相同的是 （ ）
(四) 对“点的坐标代入函数解析式”的认识
1. 将已知点的坐标代入函数解析式，构造有关系数的方程； 例33（1）（2）
2. 已知函数解析式及其图象上一点的某坐标，求这点的坐标 例33（3）
【将点的坐标代入函数解析式，构造这点另一坐标的方程】
3. 已知函数解析式及图象上一点（a，b），但a，b未知，求点坐标 例15（7）
【将点的坐标代入函数解析式，构造关于a，b的方程】
【还须一个条件，构造关于a，b的另一个方程】
4. 函数解析式中有待定系数k，点的某坐标a不知道，求函数解析式及点的坐标
【将点的坐标代入函数解析式，构造关于a，k的方程】 例33（4）
5. 用函数解析式中待定系数a、b表示点的坐标，将点的坐标代入另一函数解析式，构造关于a，b的方程
6. 求两个已知函数图象的交点坐标.
【解这两个函数解析式联立的二元一次方程组】
(五) 构造函数解析式中待定系数的方程的方法：
1. 利用函数的定义（隐含它们最高项的系数 ≠ 0）
— 一次函数 x的最高指数
= 1
函数定义 —— 二次函数 x的最高指数
= 2
— 反比例函数 x的指数 = - 1
2. 函数图象上一点坐标满足函数解析式（注意转化点的坐标）
【待定系数法构造关于“系数”方程的主要方法】
3. 利用题目的条件直接构造方程
【用含有待定系数的代数式表示点的坐标】
如，二次函数图象的顶点在x轴上（令 y = 0，Δ ≥ 0 ） 例35
4. 利用几何中公式、定理做为等量关系构造方程 例49
【用含有待定系数的代数式表示线段长】
如，面积公式、勾股定理、相似三角形对应边成比例 等
5. 利用图形中的等量关系构造方程 如， 线段和差 等 例25
(六) 学会分析方法：
如，函数中的待定系数
已知
转化点
文字——符号
的坐标 几何条件
点的坐标 已知的等量关系
代入函数
用系数的代数
解析式 式表示 …
构造关于系数 ( 如，a、b ) 的方程
(如， 定c 待a 、b ) 待定的系数越少越好
定系数 ( 如，a、b、c ) 的值
求函数解析式（如，y = ax2 + bx + c ( a ≠ 0 ) ）