2008年函数总复习题
海淀区教师进修学校 方 菁
[典型例题与练习]
平面直角坐标系
例1（1）(上海市2007) 已知a<b<0，则点A(a-b，b)在第_______象限．
（2） (沈阳市2007) 若点P(a，b)在第四象限，则点Q(b，-a)在第______象限．
（3） (贵阳市，2007) 若点M ( 1 + a，2b – 1 ) 在第二象限，则点
N ( a - 1，1 - 2b ) 在第 象限.
（4） (哈尔滨市2007) 已知坐标平面内点A(m，n)在第四象限，那么点B(n，m)在( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
例2 已知点M（3x + 2, -x - 2）在第三象限，则x的取值范围为 .
例3 （广西，2007）已知点( 2m, m – 4 )在第四象限，且m为偶数，则m的值是 .
例4 (海南省2007) 如果点A(m，n)在第三象限，那么点B(0，m + n)在 ( )
(A)x轴正半轴上 (B)x轴负半轴上 (C)y轴正半轴上 (D)y轴负半轴上
例5 已知点Q（2m2 + 4, m2 + m + 6）在第一象限的角平分线上，则m = .
例6 （1） (常州市2007) 点A(-1，2)关于y轴的对称点的坐标是 _______；点A关于原点的对称点的坐标是________．
（2） 已知点A (a, -7), B ( 5, b), 若A﹑B两点关于x轴对称，
则a = ，b = .
（3） (北京市朝阳区，2007) 若点P(m，2)与点Q(3，n)关于原点对称，则m、n的值分别是 、 .
（4） (山东省2007) 将一张坐标纸折叠一次，使得点 (0，2) 与 (-2，0) 重合，则点(
，0)与_______重合．
（5）（辽宁省，2007）已知a < 0，那么点P ( - a2 - 2, 2 – a ) 关于x轴的对称点P’在第 象限.
（6）(宁夏回族自治区2007) 点(-1，4)关于坐标原点对称的点的坐标是 ( )
(A) (-1，-4) (B) (1，-4) (C) (1，4) (D) (4，-1)
（7） (北京市石景山区，2007)点P(2，-3)关于y轴的对称点的坐标是( ).
（A）(2，3) （B）(-2，-3) （C）(-2，3) （D）(-3，2)
例7 （1） (广州市2007) 点P在第二象限，若该点到x轴的距离为
、到y轴的距离为1，则点P的坐标是
( )
(A) (-l，) (B)
(-，1) (C) (，-1) (D) (1，)
（2） 点P坐标为 ( 2 - a，3a + 6 )，且点P到两坐标轴的距离相等，则点P的坐标是( ).
（A）(3，3) （B）(3，-3) （C）(6，-6) （D）(3，3)或(6，-6)
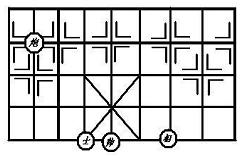
例8 (海口市课改实验区2007) 如图：如果“士”所在位置的坐标为 (-1，-2)， “相” 所在位置的坐标为(2，-2)，那么，“炮”所在位置的坐标为________．
例9 ★★ (四川省郫县课改实验区2007) 在上面的网格图中按要求画出图形，并回答问题：
(1) 先画出△ABC向下平移5格后的△
，再画出△ABC以点0为旋转中心，沿顺时针方向旋转
后的△
；
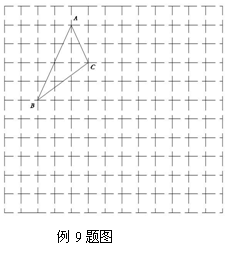(2) 在与同学交流时，你打算如何描述(1)中所画的△的位置?
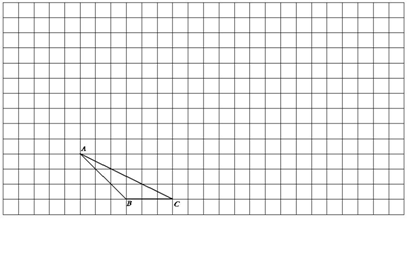
例10 ★★ (海口市课改实验区2007) (1)请在如图所示的方格纸中，将△ABC向上平移3格，再向右平移6格，得△，再将△绕点
按顺时针方向旋转，得
△
，最后将△以点
为位似中心放大到2倍，得△
；
(2) 请在方格纸的适当位置画上坐标轴(一个小正方形的边长为1个单位长度)，在你所建立的直角坐标系中，点C、
、的坐标分别为：点C(_____)、点 (_____)、
点 (_____)．
函数及其图象
例11 （1）
(北京市2007) 在函数y =
中，自变量x的取值范围是__________．
（2）(苏州市2007) 函数y =
中自变量x的取值范围是________．
（3）(常州市2007) 在函数y =
中，自变量x的取值范围是_______．
（4）(山东省潍坊课改实验区2007)
函数y =
自变量x的取值范围是______．
（5）(甘肃省2007) 在函数y = 
中，自变量x的取值范围是 ( )
(A) x≥4 (B) x≤4 (C) x>4 (D) x<4
（6）(广州市2007) 函数y=
中，自变量x的取值范围是 ( )
(A) x≥o (B) x>0且x≠l (C) x>O (D)x≥o且x≠1
例12（1） 已知y = 
，当x = 3 时，y = ，当 x = 
时，y = .
（2） 已知 y = -3x + 2，当 y = 4时，x = .
例13 已知 函数 y = 5x + 2，不画图象，判断点 (-2, -8)、(-1, 3)、(-
,0)、(0,)在不在这个函数图象上.
例14（1） (泰州市，2007)为了加强公民的节水意识，某市制定了如下用水收费标准：每户每月的用水不超过l0t时，水价为每吨1．2元；超过l0t时，超过的部分按每吨1．8元收费．该市某户居民5月份用水xt(x>10)，应交水费y元，则y关于x的关系式是 。
（2）(曲靖市，2007)公民的月收入超过1000元时，超过部分须依法缴纳个人
所得税，当超过部分在500元以内(含500元)时税率为5％，那么公民每月所纳税款y(元)与月收入z(元)之间的函数关系式是 ，（不用写出自变量取值范围）.某人月收人为1360元，则该人每月应纳税 元．
（3）(呼和浩特市，2007)等腰△ABC周长为l0cm，底边BC长为ycm，腰AB长
为xcm． ①写出y关于x的函数关系式；②求x的取值范围；③求y的取值范围·
一次函数
1.一次函数的解析式与图象上点的坐标【用方程思想】
|
|
（2）(河南省2007) 点M(-2，k)在直线y=2x+1上，M到x轴的距离d=_______．
（3）若一次函数图象过A (2, -1)和B两点，其中点B是另一条直线y =﹣
x + 3与y 轴的交点，求这个一次函数的解析式.
（4） 已知两条直线 y1 = (m – 1)x + m2 – 5 与 y2 = x – 1的交点恰在y轴上，且y1随x增大而减小，写出y1与x之间的函数关系式及此直线与两坐标轴的交点坐标.
（5）直线y = kx + b 与直线y = 5﹣4x平行，且与直线y = ﹣3（x﹣6）相交，交点恰在y轴上，求这条直线的函数解析式.
（6）直线与x轴交于点A（﹣4，0），与y轴交于点B，若点B到x轴的距离为2，求这条直线的函数解析式.
（7）已知 y = 3x – 2 的图象经过点（ a，b ），且 a + b = 6，求a、b的值.
2. 一次函数中的数形结合【用数形结合思想】
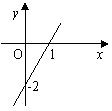例16 （1）（贵阳市课改实验区2007）已知一次函数y=kx+b的图象（如图），当x＜0时，y的取值范围是
（A）y ＞ 0 （B）y ＜ 0
（C）- 2 ＜ y ＜ 0 （D）y ＜ - 2
（2） （福州市2007）已知正比例函数y = kx （k≠0）过第二、四象限，则 （ ）
（A）y随x的增大而减小 （B）y随x的增大而增大
（C）当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而减小
（D）不论x如何变化，y不变
例17 新课程标准P36 例11
填表并观察下列两个函数的变化情况：
| X | 1 | 2 | 3 | 4 | 5 | … |
| Y1 = 50 + 2x | ||||||
| Y2 = 5x |
（1） 在同一个直角坐标系中画出上面两个函数的图象，比较它们有什么不同；
（2） 当 x 从1开始增大时，预测哪一个函数的值先到达100.
3．图形的移动（翻转，平移，旋转）
例18 （四川省含成都市2007）在平面直角坐标系中，直线y=kx+b（k，b为常数，k≠0，b＞0）可以看成是将直线y=kx沿y轴向上平行移动b个单位而得到的，那么将直线y=kx沿x轴向右平行移动m个单位（m＞0），得到的直线方程是 .
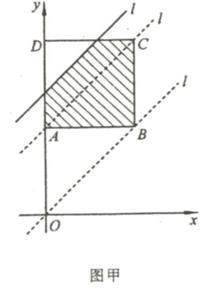
例19 （河南省2007）如图甲，边长为2的正方形ABCD中，顶点A的坐标是(0，2)．一次函数y = x + t的图像l随t的不同取值变化时，位于l的右下方由l和正方形的边围成的图像面积为S（阴影部分）
（1） 当t取何值时，S=3
（2） 在平面直角坐标系下（如图乙），画出S与t的图像。
 |
4. 与一次函数有关的实际问题
例20 （山东省潍坊课改实验区2007）已知某山区的平均气温与该山的海拔高度的关系见下表：
| 海拔高度（单位“米”） | 0 | 100 | 200 | 300 | 400 | … |
| 平均气温（单位“°C”） | 22 | 21.5 | 21 | 20.5 | 20 | … |
（1） 若海拔高度用x（米）表示，平均气温用y（°C）表示，写出y与x之间的函数关系式；
（2） 若某种植物适宜生长在18°C~20°C（包含18°C，也包含20°）的山区，请问该植物适宜种植在海拔为多少米的山区？
例21 （甘肃省2007）甲、乙两人在一次赛跑中，路程s与时间t的关系如图所示（实线为甲的路程与时间的关系图像，虚线为乙的路程与时间的关系图像），小王根据图像得到如下四个信息，其中错误的是： （ ）
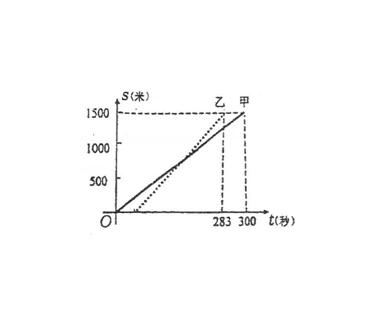(A) 这是一次1500米的赛跑
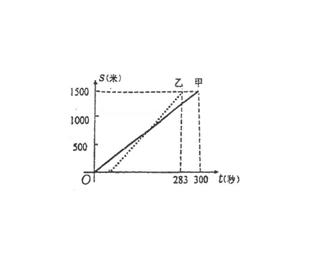(B) 甲、乙两人中先到达终点的是乙
(C) 甲、乙同时起跑
(D) 甲在这次赛跑中的速度为5m/s
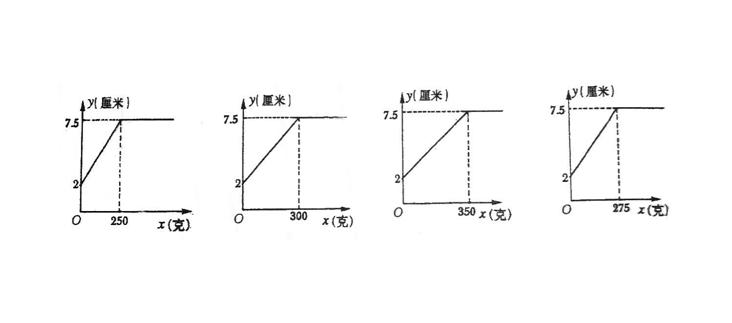例22 （黄冈市2007）某班同学在探究弹簧的长度跟外力的变化关系是，实验记录得到的相应数据如下表：
| 砝码的质量 （x克） | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 指针的位置 （y厘米） | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
则y关于x的函数图像是： （ ）
(A) (B) (C) (D)
例23 （1） ★★（沈阳市2007）某市的A县和B县春季育苗，急需化肥分别为90吨和60吨，该市的C县和D县分别储存化肥100吨和50吨，全部调配给A县和B县，已知C、D两县运化肥到A、B两县的运费（元/吨）如下表所示。
|
运费 目的地 | C | D |
| A | 35 | 40 |
| B | 30 | 45 |
出 发 地（1） 设C县运到A县的化肥为x吨，求总运费W元与x吨的函数关系式，并写出自变量x的取值范围；
（2） 求最低总运费，并说明总运费最低时的运送方案。