九年级数学函数总复习题3

2008年函数总复习题

海淀区教师进修学校　　　 方　 菁　　　2008.3.25

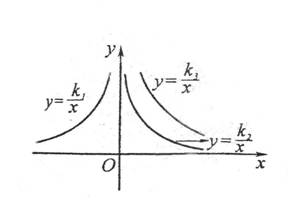（3）（河南省2007）如图是三个反比例函数y = 、y = 、y = 在x轴上方的图像，由此观察得到k₁、k₂、k₃的大小关系为（　  ）

　　　　　　　　　　　　　　　　　　　　　　 　　　　　 

(A) k₁ > k₂ > k₃　　 (B) k₂ > k₃ > k₁

(C) k₃ > k₂ >k₁　　　　(D) k₃ > k₁ > k₂

3. 反比例函数的应用

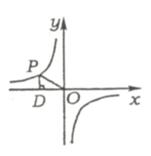例31（南昌市2007）如图，点P是反比例函数y = 上的一点，PD⊥x轴于点D，则△POD的面积为_______.

4. 相关的综合题

例32 （1）（辽宁省2007年）已知一次函数 y = kx + b的图象经过第一、二、四象限，则反比例函数 y = 的图象是（  ）.

(A) 第一、二象限　　　　  (B) 第三、四象限

 (C) 第一、三象限　　　　  (D) 第二、四象限

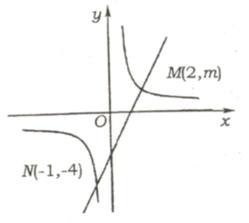
（2）（贵阳市课改实验区2007）如图，一次函数y = ax + b的图像与反比例函数y = 的图象交于M、N两点

　　　　1）求反比例函数和一次函数的解析式；

　2）根据图象写出使反比例函数的值大于一次函数的值的x的取值范围。

（3）（镇江市2007）已知一次函数y = kx + k的图象与反比例函数y = 的图象交于点P（4，n）。

1）求n的值。　　 2）求一次函数的解析式。

二次函数

1.　　  二次函数解析式与它图象上的点【用方程思想】

例33（1）抛物线 y = 2x² + bx – 5 过点A ( - 2, 9 )，则关于“b”的方程为　　　　　  ，此抛物线的解析式为　　　　　  .

（2）（安徽省2007年）已知函数 y = x² + bx – 1 的图象经过点（3，2）.

 1）求这个函数的解析式；

2）画出它的图象，并指出图象的顶点坐标；

（3）抛物线 y = 2x² - 3x – 5 过点A ( n, 9 )，则关于“n”的方程为　　　　　  ，解得 n = 　　.

（4）抛物线 y = 2x² + bx – 5 过点A ( - 2, y_A )，则 y_A = 　　　　 

（5） 二次函数 y = ax² + bx+ c的图象的顶点A 的坐标为 ( 1, - 3 )，且经过点 B ( -1, 5 )，则设 y = 　　　　　, 得方程为  　　　　，解得　　　　，此函数解析式为 　　　　　　 . （优选顶点式）

（6）二次函数 y = ax² + bx + c的图象与 x 轴交于点A ( - 3, 0 )，对称轴x = -1，顶点C到x轴的距离为2，则设 y = 　　　　　　　, 得方程为　　　　　　 ，解得　　　　　  ，此函数解析式为 　　　　　　　　　 .　（优选顶点式）

例34（1） y = - 2x² + 5x – 3 与 y轴的交点的坐标为　 　　　，

（2） y = 2x² – 5x + c 与 y 轴的交点为（ 0，3 ），则有c = 　　　 .

（3） y = - 2x² + 5x – 3 与x 轴的交点坐标为　　　　 、　　　　 .

（4）（安徽省2007年）已知函数 y = x² + bx – 1 的图象经过点（3，2）.　

1）求这个函数的解析式；

2）画出它的图象，并指出图象的顶点坐标；

例35　（1）（常州市2007年）抛物线y = x² - 6x + c 的顶点在 x轴上，则 c 的值是（  ）.

（A） 9　　（B） 3　　 （C） - 9　　 （D） 0

（ 顶点在 x轴上、抛物线与轴相切、抛物线与轴有且仅有一个交点

←　　 →　　　 △ = b² – 4ac = 0）

（2）抛物线 y = - x² + 4x + n - 2 的顶点 P 在 x 轴上，求此抛物线与两坐标轴的交点的坐标.

例36（1）  抛物线y = - 2 ( x – 3 )² – 7 对称轴 x = 　　 ,

顶点坐标为　　　　  ；

（2）　抛物线 y = 2x² + 12x – 25 化为　　　　　　　　 ,

对称轴 x = 　　　　　, 顶点坐标为　　　　　　 .

（3）（河北省2007）若将二次函数y=x²－2x + 3配方为y =（x－h）² + k的形式，则y=　　　　　

（4）（贵州市课改实验区2007）抛物线y= - 4（x+2）²+5的对称轴是　　　　　 。

2.　　  二次函数中的数形结合【用数形结合思想】

例37（1） 抛物线 y = - 3x² + 5x - 4开口　　　 , 

y = 4x² – 6x + 5 开口　　　　.

（2）已知： 二次函数 y = ( m – 3 ) x² + 2mx + m + 2，其中m 为常数，且满足-2 < m < 3，此抛物线的开口　　 ，与 x 轴　　　 交点（填有、无），与 y 轴的交点在x 轴　　　　（填上方、下方）.

　  （3） 如果二次函数y = 2x² + ( 2a – b )x + b，当且仅当

 1 < x < 2 时，y < 0，那么 a、b 的值是　　　　　 .

（4）（天津市2007）已知二次函数y=ax²+bx+c，且a＜0，a-b+c＞0，则一定有　（　　　）

（A）b² - 4ac＞0　　　（B）b² - 4ac=0　　 （C）b² - 4ac＜0　（D）b² - 4ac≤0

例38 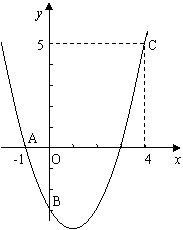（沈阳市2007）如图，二次函数y=ax²+bx+c的图象经过A、B、C三点.

1）观察图象写出A、B、C三点的坐标，并求出此二次函数的解析式；

2）求出此抛物线的顶点坐标和对称轴。

	-3

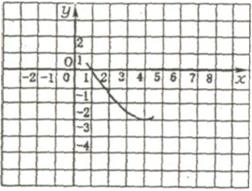
例39 （1）（贵阳市课改实验区2007）已知抛物线y=(x - 4)² - 3的部分图像(如图) 图像再次与x轴相交时的坐标是　　　　　　　　　　　　　　　　　　   （　　 ）

(A)　(5，0)　　　 (B)　(6，0)　　　　 (C)　(7，0)　　　　 (D)　(8，0)

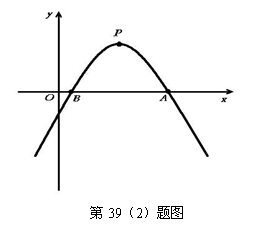
（2） (昆明市2007) 如图，已知二次函数y= (a≠0)的图象的顶点P的横坐标是4，图象交x轴于点A(m，0)和点B，且m>4，那么AB的长是　  (　　)

　　(A)4+m　　　 (B)m　 　　 (C)2m一8　　　 (D)8—2m