立体图形与平面图形
一、立体图形
1. 柱体
棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫棱柱.
圆柱:以矩形的一边所在直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆柱.
2. 锥体
棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫棱锥.
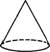
圆锥:以直角三角形一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥.
3. 球体
半圆以它的直径为旋转轴,旋转所成的曲面所围成的几何体叫球体.
4. 多面体
围成棱柱和棱锥的面是平的面,像这样的立体图形叫多面体.
棱柱有三棱柱、四棱柱、五棱柱等.棱锥也有三棱锥、四棱锥、五棱锥等.
二. 画立体图形
1. 三视图法
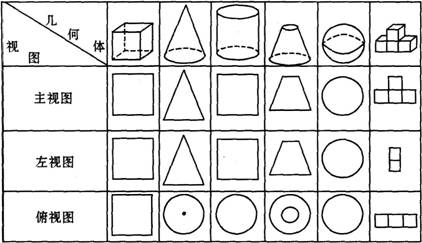
从正面、上面和侧面(左面或右面)三个不同的方向看一个物体,然后描绘三张所看到的图,即视图,这样就把一个物体转化为平面的图形.
从正面看到的图形称为正视图;从上面看到的图形称为俯视图;从侧面看到的图形称为侧视图,按观察方向不同,有左视图,右视图.
注:⑴正视图与俯视图的长度相等,且相互对正,即“长对正”;
⑵ 正视图与侧视图的高度相等,且相互平齐,即“高平齐”;
⑶ 俯视图与侧视图的宽度相等,即“宽相等”.
2. 欧拉公式
多面体具有的顶点数,棱数和面数满足欧拉公式:
顶点数+面数-棱数=2
三、柱体、锥体的展开
| 名称 | 几何体图形 | 平面展开图 | 底面形状 | 侧面展开形状 |
| 正方体 |
|
| 正方形 | 长方形 |
| 圆锥 |
|
| 圆 | 扇形 |
| 圆柱 |
|
| 圆 | 长方形 |
四、常见几何体的主视图
【典型例题】
例1. 下列说法是否正确?正确的打“√”,不正确的打“×”,并简要说明理由.
(1)柱体的上、下两个面一样大
(2)圆柱和圆锥的底面都是圆,圆柱的侧面是长方形,圆锥的侧面是三角形
(3)棱柱的底面是四边形,侧面可能是三角形
(4)棱锥的侧面都是三角形
(5)球体、圆柱、圆锥都不是多面体.
分析:要对以上各种说法作出正确的判断,应从熟悉柱体、锥体、球体这些立体图形入手,把握它们各自的特征,弄清它们之间的区别.
解:(1)√.柱体包括圆柱和棱柱.圆柱的两个底面都是大小一样的圆,棱柱两个底面都是一样大的三角形或多边形.
(2)×.圆柱和圆锥的侧面都是弯曲的面.而长方形、三角形都是平的面,两者显然有区别.
(3)×.棱柱的底面除了四边形以外,还可以是三角形等其它图形,棱柱的侧面都是四边形.
(4)√.棱锥的所有棱都交于一点,侧面都是三角形.
(5)√.多面体都是由平的面围成的立体图形,而球体、圆柱、圆锥并不都是由平面围成的.
说明:留心生活中的物体,并能从中抽象出立体图形,除了注意不同类立体图形的区别,更应注意同类立体图形的细微差别.
例2. 能否组成一个22条棱,10个面,15个顶点的棱柱或棱锥?为什么?
分析:本题很难利用图形作出判断、考虑到棱柱或棱锥都是多面体,多面体都应满足“欧拉公式”.
解:根据欧拉公式,顶点数+面数-棱数=2
当顶点数为15,面数为10时,棱数应为:![]()
因此,不能组成一个棱数为22,面数为10,顶点数为15的棱柱或棱锥.
说明:欧拉公式体现了多面体中顶点数、面数与棱数之间的关系,已知其中的两个数就可以求出第三个数.另外,还可以用它来判断具有某些条件的多面体是否存在.
例3. 填空
正方体是由_________个顶点,_________条棱,_________个面组成的,它还具有以下特点(写出三个)___________________________.
解:正方体是由8个顶点,12条棱,6个面组成的,它还具有以下特点:所有的棱都相等,所有的面都是正方形,它是一个多面体.(或柱体、四棱柱等)
例4. 用火柴摆出正方形,用多少根火柴才能摆出6个正方形?尽可能多地设想各种方案.并画出你的图形.(要求摆出的6个正方体的边长限于一根火柴的长)
解:第一种方法:摆平面图形
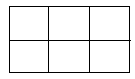
需要用17根火柴.
第二种方法:摆三棱柱
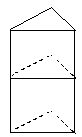
需要用15根火柴.
第三种方法:摆正方体
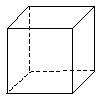
需要用12根火柴.
例5.如图,下面是一个物体的三视图,试描述该物体的形状.

分析:由物体的三视图想象物体的形状,要几个视图联系起来看.从正视图中可看出它是由两个部分叠加或是左边挖掉了一个形体,再对照俯视图,左视图便可知道右边上面加了半个圆柱体,圆柱下面是一个长方体,并且圆柱体的左面与长方体左面平齐,柱体的底面直径与长方体的宽一样.
解:该物体的形状如图所示:

说明:由视图想象物体的形状一般按以下步骤进行:
(1)分线框,把几个视图联系起来看,把物体大致分成几部分;(2)识形体,定位置,根据每一部分的视图想象出它的形体,并确定它们的相互位置;(3)综合起来想整体,确定各个部分的形体及相互位置后,整个物体的形状也就清楚了.
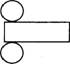
例6. 如图所示是一个几何体的两个视图,求该几何体的体积(![]() 取3.14,长度单位cm)
取3.14,长度单位cm)
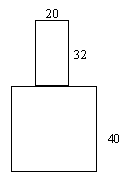
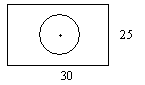
正视图 俯视图
分析:从所给两个视图可以确定,设几何体是由两部分组成的,下面是一个长方体,它的长、宽、高分别是30cm、25cm、40cm.上面是一个圆柱体,底面圆的直径是20cm,长为32cm,所以该几何体的体积是这两部分体积之和.

解:长方体体积为:30×25×40=30000cm3
圆柱体体积为:3.14×102×32=10048 cm3 30000+10048=40048cm3
答:几何体体积为![]() .
.
例7. 如图所示的立方体,将其展开得到的图形是( )


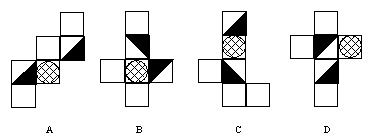 (例8图)
(例8图)