九年级数学第三章测试题
班级 姓名 号次
一、填空题：（38%，1——6题每一个空格1分，第7题3分。）
1、二次函数
中，二次项系数是 ，一次项系数是 ， 常数项是 。
2、二次函数
中，图象是 ，开口 ，对称轴是直线 ，顶点坐标是（ ），当X
时，函数Y随着X的增大而增大，当X 时，函数Y随着X的增大而减小。当X= 时，函数Y有最 值是 。
3、抛物线
中，对称轴是 ，图象与Y轴的交点是（
），这点关于对称轴的对称点的坐标是（
），图象与X轴的交点的坐标是（ ），（
）。当X 时，Y=0，当 X 时，Y〈0，当X 时，Y〉0。
4、抛物线
，是由抛物线 ，先向 平移
单位，再向
平移
单位得到的。
5、已知函数
当
时，图象是直线；当 
时，图象是抛物线；当
时，抛物线过坐标原点。
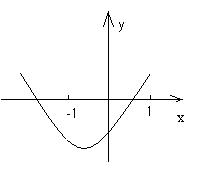
6、已知抛物线
（如图），与
轴交于
点A
则
的符号是 ，
的符号是
，
的符号是
，
的是 ，
的符号是 ，
的符号是 ，
的符号是 。
7、用配方法把二次函数
化成
的形式，即
。
二、选择题：（30%）
1、在同一坐标系中，三条抛物线
的共同点是（
）
A、关于轴对称，开口向上；
B、关于轴对称，
随的增大而增大；
C、关于轴对轴，顶点在原点； D、关于轴对称，随的增大而减少。
1
2、在函数
，以为自变量的二次函数有（
）
A、1个； B、2个； C、3个； D、4个。
3、二次函数
的图象与轴的交点个数是（
）
A、1个； B、2个； C、1个或者2个； D、0个。
4、周长为30的等腰三角形，设腰长为，则的取值范围为（ ）
A、
；
B、
；
C、
D、
。
5、二次函数
，当
时的取值范围是（ ）
A、
； B、
； C、
；
D、或。
6、二次函数的图象的对称轴位置（
）
A、只与有关；
B、只与有关；
C、只与
有关； D、与
都有关。
7、一元二次方程
的两根为-3，-1，则抛物线的对称轴是（
）
A、直线
；
B、直线
；
C、直线
；
D、直线
。
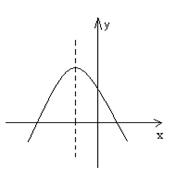
8、已知二次函数的图象如图，
则在“①
②
③
④
”
正确的个数是（ ）
A、1； B、2； C、3； D、4。
9、如果抛物线
的顶点在轴的下方，那么是（
）
A、大于零； B小于零； C大于等于零； D、小于等于零。
10、一个二次函，当
时，
；当时，
；当时，
，
这个二次函数解析式是（ ）
A、
；
B、
；
C、
；
D、
。
三、解答题：（32%）
1、已知二次函数
的顶点坐标为（-1，-3），求
的值。
2
2、已知二次函数的图象过点（4，-3），且当
时，
，求这个二次函数的解析式。
3、如图，用长20米的篱笆，一面靠墙围成一个长方形的园子，怎样围才使园子的面积最大？最大面积是多少？
4、已知二次函数
。
（1） 证明不论为何实数，二次函数的图象与轴有两个交点；
（2） 当函数图象经过点（3，6）时，确定的值。
3
（住宿必做）
5、抛物线
的顶点为（-2，1），且 两根之差的绝对值等于2，求抛物线的函数解析式。（8%）
6、已知二次函数
。
（1）
当它的图象与轴交于点A（0，5）时，求
的值；
（2）
对于（1）所求出的二次函数，设其图象与的交点从左到右依次是B，C，若点P
是BC上的一个动点（可以与B重合，但不能与C重合），点D的坐标为（0，3），写出四边形ADPC的面积S关于的函数关系式；
（3）
当为何值时S最大，这个最大值是多少？
4