初三数学上学期期中考试试卷
(100分钟完成,满分150分)
| 题号 | 一 | 二 | 三 | 四 | 总分 |
| 得分 |
一、填空题(每小题3分,满分36分)
1.
方程![]() 的根是______________.
的根是______________.
2.
方程![]() 的根是________________.
的根是________________.
3.
分解因式:![]() _______________________.
_______________________.
4.
在公式![]() 中,已知正数R、R1(
中,已知正数R、R1(![]() ),那么R2=
.
),那么R2=
.
5.
用换元法解方程![]() 时,可设y=
时,可设y=![]() ,那么原方程可化为关于y 的整式方程是
.
,那么原方程可化为关于y 的整式方程是
.
6.
某电子产品每件原价为800,首次降价的百分率为![]() ,第二次降价的百分率为2
,第二次降价的百分率为2![]() ,那么经过两降价后每件的价格为_____________________元(用
,那么经过两降价后每件的价格为_____________________元(用![]() 的代数式表示).
的代数式表示).
7.
![]() 如图1,已知舞台
如图1,已知舞台![]() 长10米,如果报幕员从点
长10米,如果报幕员从点![]() 出发站在舞
出发站在舞
台
|
报 幕(
幕(![]() ,结果精确到0.1米).
,结果精确到0.1米).
8.
如图2,在![]() 中,点D、E分别在边AB、AC上,DE∥BC,
中,点D、E分别在边AB、AC上,DE∥BC,![]() ,则
,则![]() .
.
9.
|
∠B=![]() ,则∠F=
.
,则∠F=
.
10.
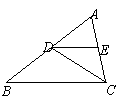 在△ABC中,点D、E分别在边AB、AC上,要使△ADE与△ABC相似,只须添加一个条件,这个条件可以是___________(只要填写一种情况) .
在△ABC中,点D、E分别在边AB、AC上,要使△ADE与△ABC相似,只须添加一个条件,这个条件可以是___________(只要填写一种情况) .
11.
在△ABC中,中线AD和CE相交于G,则![]() _________.
_________.
12. 如图3, 在△ABC中, 点D、E分别在AB、AC上,DE//BC,
|
二、选择题(每小题4分,满分16分)
13. 下多项式中,在实数范围内能分解因式的是………………………………………( )
(A)![]() ; (B)
; (B)![]() ;
;
(C)![]() ; (D)
; (D)![]() .
.
14. 下列方程中, 有实数根的是………………………………………………………( )
(A)![]() ;
(B)
;
(B)![]() ;
;
(C)![]() ;
(D)
;
(D)![]() .
.
15. 如果点D、E分别在ΔABC的两边AB、AC上,下列条件中可以推出DE∥BC的是( )
(A) = ,= ; (B) = ,= ;
(C)
= ,= ;
(D) =![]() ,=
,= ![]() .
.
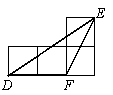
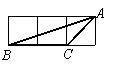
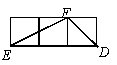
16. 如图4,小正方形的边长均为l,△ABC与△DEF的顶点都在小正方形的顶点上,则
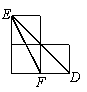 △DEF与△ABC相似的是……………………………………………………………( )
△DEF与△ABC相似的是……………………………………………………………( )
 | |||||||
 |  | ||||||
 | |||||||
|
三、(第17、18题每小题9分,第19、20、21题每小题10分,满分48分)
17.解方程:![]() .
.
18.方程组: 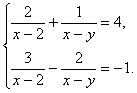
19. 函数![]() 图象上一点P的纵坐标比横坐标多1, 求这个点的坐标.
图象上一点P的纵坐标比横坐标多1, 求这个点的坐标.
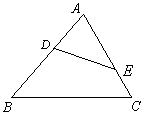 20. 如图5,在△abc中,点D、E分别在边AB、AC上,
20. 如图5,在△abc中,点D、E分别在边AB、AC上,![]() ,且
,且![]() 厘米,
厘米,![]() 厘米,
厘米,![]() 厘米,求线段
厘米,求线段![]() 的长.
的长.
|
 21.已知:如图6,在四边形ABCD中,AD//BC,点E在边CD上,AE的延长线与BC的延长相交于点F,
21.已知:如图6,在四边形ABCD中,AD//BC,点E在边CD上,AE的延长线与BC的延长相交于点F,![]() .
.
求证:∠D=∠B.
|
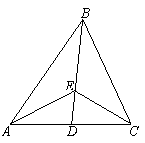 四、(第22、23、24题每小题12分,第25题14分,满分50分)
四、(第22、23、24题每小题12分,第25题14分,满分50分)
22.已知:如图7,△ABC中,点E在中线BD上, ![]() .
.
求证:(1)![]() ; (2)
; (2)![]() .
.
|
23.现有甲、乙两辆货车将一批货物从A地运往B地,每车都装满,乙车比甲车每车多运2吨, 甲车运200吨比乙车运200吨要多运5次,求甲、乙两辆货车每次各运几吨.
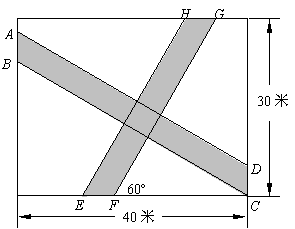
24.如图8,有一块长为40米,宽为30米的长方形绿地.其中有两条互相垂直的笔直的道路(图中的阴影部分),道路的一边GF与长方形绿地一边的夹角为60º,且道路的出入口的边AB、CD、EF、GH的长度都相同,已知道路面积为137平方米,求道路出入口的边的长度.
|
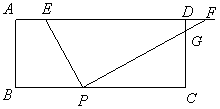 25. 在矩形
25. 在矩形![]() 中,
中,![]() ,
,![]() ,点P在BC上,且
,点P在BC上,且![]() ,动点
,动点![]() 在边
在边![]() 上,过点
上,过点![]() 作
作![]() 分别交射线
分别交射线![]() 、射线
、射线![]() 于点
于点![]() 、
、![]() .
.
|
 (2) 当点E在移动过程中,△DGF是否可能为等腰三角形?如可能,请求出AE的长;如不可能,请说明理由.
(2) 当点E在移动过程中,△DGF是否可能为等腰三角形?如可能,请求出AE的长;如不可能,请说明理由.
初三数学期中考试试卷参考与评分意见
一、1.![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() 4.
4. ![]() ;
;
5. ![]() 6.
6. ![]() ; 7. 3.8 ; 8. 2:5 ;
9. 60º或70º;
10. 可填DE//BC或∠AED=∠B或
; 7. 3.8 ; 8. 2:5 ;
9. 60º或70º;
10. 可填DE//BC或∠AED=∠B或![]() 等; 11. 2:3; 12. 3:4.
等; 11. 2:3; 12. 3:4.
二、13.D; 14. B; 15. C; 16. B.
三、17.解:![]() ,(3分)
,(3分) ![]() (2分)
(2分)
![]() ,(2分)
,(2分)
经检验:![]() 是原方程的根,
是原方程的根,![]() 是增根.(2分)
是增根.(2分)
所以原方程的根是![]() .
.
18. 解:设![]() ,
,![]() (1分) 则原方程组可化为
(1分) 则原方程组可化为![]() (2分)
(2分)
解此方程得![]() (2分) ∴
(2分) ∴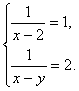 (1分) ∴
(1分) ∴ 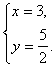 (2分)
(2分)
经检验: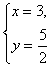 是原方程组的解,∴所以原方程组的解是
是原方程组的解,∴所以原方程组的解是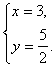 (1分)
(1分)
19. 解:设点![]() ,(2分)
,(2分) ![]() ,(2分)
,(2分) ![]() ,(2分)
,(2分)
![]() ,(2分) ∴点P的坐标为
,(2分) ∴点P的坐标为![]() 或(
或(![]() .(2分)
.(2分)
20.解:∵![]() ,
,![]() ,(1分) ∴
,(1分) ∴![]() ∽
∽![]() .(2分)
.(2分)
∴![]() .(2分) ∵
.(2分) ∵![]() 厘米,
厘米,![]() 厘米,
厘米,![]() 厘米,
厘米,
∴![]() ,(2分) 解得
,(2分) 解得![]() .(2分) ∴
.(2分) ∴![]() 厘米.(1分)
厘米.(1分)
21. 证明:∵![]() ,∴
,∴![]() .(2分)∵AD//BC,∴
.(2分)∵AD//BC,∴![]() (2分)
(2分)
∴![]() .(2分) ∴DE//BC.
(2分)
.(2分) ∴DE//BC.
(2分)
∴四边形ABCD是平行四边形.(1分) ∴∠B=∠D.(1分)
四、22.证明:(1)∵![]() ,
,![]() ,∴
,∴![]() ∽
∽![]() .(2分)
.(2分)
∴![]() ,(2分) 即
,(2分) 即![]() .(1分)
.(1分)
(2)∵![]() 是
是![]() 边上的中点,∴
边上的中点,∴![]() .∵
.∵![]() ,∴
,∴![]() ,(2分)
,(2分)
又∵![]() .(1分)∴
.(1分)∴![]() ∽
∽![]() .(2分)∴
.(2分)∴![]() .(2分)
.(2分)
23. 解:甲货车每次各运![]() 吨,(1分) 则乙货车每次各运(
吨,(1分) 则乙货车每次各运(![]() )吨.(1分)
)吨.(1分)
由题意得 ![]() .(3分) 化简整理得
.(3分) 化简整理得
![]() .(2分)
.(2分)
解得![]() . (2分) 经检验
. (2分) 经检验![]() 都是原方程的根,
都是原方程的根,
但![]() 不合题意舍去,(1分) ∴
不合题意舍去,(1分) ∴![]() ,
,![]() (1分)
(1分)
答:甲、乙两辆货车每次各运8吨、10吨.(1分)
24.解:道路出入口的边的长度为![]() 米.(1分)
米.(1分)
过点F作FM⊥EH,可求得EH=![]() ,可得小正方形的边长为
,可得小正方形的边长为![]() 米.(2分)
米.(2分)
![]() ,(3分)
,(3分) ![]() ,(1分)
,(1分)
![]() , (1分)
, (1分) ![]() .(2分)
.(2分)
![]() 不符合题意,舍去.(1分)
不符合题意,舍去.(1分)
答:道路出入口的边的长度为2米.(1分)
25. 解:(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() .(1分)
.(1分)
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ;
;
∵![]() ,∴
,∴![]() ;∵EH=AB=2, ∴
;∵EH=AB=2, ∴![]() ,(2分)
,(2分)
∵![]() ,∴∠EPH=90º–∠GPC=∠PGC,(1分)
,∴∠EPH=90º–∠GPC=∠PGC,(1分)
∴![]() ∽
∽![]() .(1分)∴
.(1分)∴![]() (1分)
(1分)
∴![]() .(1分)
.(1分)
∵![]() ,∴
,∴![]() ,(2分) (
,(2分) (![]() ).(1分)
).(1分)
(2)当点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() 不可能.(2分)
不可能.(2分)
当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ,
,![]() ,
,![]() .
.
此时可解得![]() ,即当点E与点A重合时,
,即当点E与点A重合时,![]() 是等腰三角形.(2分)
是等腰三角形.(2分)