初三数学
第三次月考考试试卷
(满分：120分 时间：120分钟 )
一、填空题（共30分）
1、
2、已知在⊙O中，弦AB的长为8㎝，圆心O到弦AB的距离为3㎝，则⊙O的半径是______
3、用长为4㎝,5㎝,6㎝的三条线段围成三角形的事件,是________ 事件..
4、某工厂今年利润为a万元，计划今后每年增长m﹪，两年后的利润为____________
5、若圆锥的底面半径为3㎝，母线长是5㎝，则它的侧面展开图的面积为____________.
6、用反证方法证明“在△ABC中，不能有两个钝角”的第一步是假设：
7、在数轴上与表示
的点的距离最近的整数点所表示的数是
．
8、请写出有一个解是-1的一元二次方程：__________
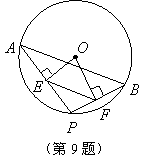
9、如图，点
⊙O是上两点，
，点
是⊙O的动点（与不重合），连结
，过点
分别作
于
，
于
，则
．
10、如图，矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E，GB=8㎝
AD=2㎝，则EF=
 | |||
 | |||
二、选择题：（18分）
11、下列各式是二次根式的是（ ） （第10题）
（A）
（B）
（C）
（D）
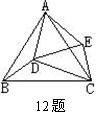
12、如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( )
（A） ΔABC和ΔADE （B） ΔABC和ΔABD
（C） ΔABD和ΔACE （D） ΔACE和ΔADE
13、已知扇形的半径是12㎝，圆心角是60°，则扇形的弧长是（ ）
（A）24 ∏㎝ （B）12 ∏ ㎝ （C）4 ∏ ㎝ （D）2∏㎝
14、已知两圆的半径分别为3㎝和4㎝，两个圆的圆心距为10㎝，则两
圆的位置关系（ ）
（A）内切 （B）相交 （C）外切 （D）外离
15、初三（1）班每一个同学都将自己的相片向全班其他同学各送一张表示留念，全班共送了2550张相片，如果全班有x名学生，根据题意，列出方程为 ( )
（ A）x(x+1)=2550 (B)x(x-1)=2550 (C)2x(x+1)=2550 (D)x(x-1)=2550×2
16、⊙O的半径为13㎝，弦AB∥CD，AB=24㎝，CD=10㎝，则AB与CD间的距离为（ ）
（Ａ）7㎝ （Ｂ）17㎝ （Ｃ）5㎝ （Ｄ）7㎝或17㎝
三、（本大题共3小题，17题6分，18、19题各7分，共20分）
17、计算：
18、解方程：x2-3x-4=0
19、如图，AB、BC、CD分别与⊙O相切于E、F、G，且AB∥CD，BO=6㎝，CO=8㎝，求BC长
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
四、（本大题共两小题，每小题8分，共16分）
20、阅读下面的解答过程，请判断其是否有错，请你写出正确解答：
已知：m是关于x的方程mx2-2x+m=0的一个根，求m的值。
解：把x=m代入原方程，化简得m3=m，
两边同时除以m得：m2=1
所以： m=1
把m=1代入原方程检验可知，
m=1符合题意。
答：m的值是1
21、布袋中有红、黄、蓝三种颜色的球各一个,
(1)从中先摸出一个球,记录下它的颜色,将它放回布袋,搅匀,再摸出一个球,记录下颜
色,求得到的两个颜色中有“一红一黄”的概率;
(2)如果摸出第一个球后不放回布袋,再摸第二个球,这时得到的两个颜色中有“一红一
黄”的概率是多少?
五、（本大题共2小题，第22小题8分，第23小题9分，共17分）
22、要设计一本书的封面，封面长27㎝，宽21㎝，正中央是一个与整个封面长宽比例相
同的矩形，如果要使四周的彩色边衬所占面积是封面面积的四分之一，上、下边衬等
宽，左右边衬等宽，应如何设计四周边衬的宽度？（保留根号）
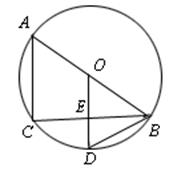
23、如图，AB是圆O的直径，BC是弦，OD⊥BC于E，交BC于D。
（1）请写出四个不同类型的正确结论；
（2）连结CD，设∠CDB=α，∠ABC=β，试找出α与β之间的一种关系式，并给予证明。
六、（本大题共2小题，第24小题9分，第25小题10分，共19分）
24、某地方有座弧形的拱桥，如图，桥下的水面宽为7.2米,拱顶高出水面2.4米,现有一
艘宽3米,船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这
座拱形桥吗?
 | |||||
 | |||||
 | |||||
25．在同一平面直角坐标系中有6个点：
，
，
．
（1）画出
的外接圆⊙P，并指出点
与⊙P的位置关系；
（2）若将直线
沿
轴向上平移，当它经过点时，设此时的直线为
．
①判断直线与⊙P的位置关系，并说明理由；
②再将直线绕点按顺时针方向旋转，当它经过点
时，设此时的直线为
．求直线与⊙P的劣弧
围成的图形的面积（结果保留
）．
万年二中第三次考试试卷答案
初 三 数 学
一、填空题
1、3
2、5㎝
3、必然事件
4、a（1+m﹪）2 5、15∏㎝2
6、假设△ABC中有两个角是钝角 7、3 8、略 9、5 10、4
二、选择题:
11-16 C C C D B C
三、17、0 18、x1=4 x2=-1 19、10㎝
四、20、解: 把x=m代入原方程化简得m3-m=0 ∴ m(m2-1)=0 ∴m(m+1)(m-1)=0
∴m=0或m+1=0或m-1=0 ∴m1=0 m2=-1 m3=1
21、(1) 
(2) 
五、22、解:设中央矩形的长与宽的比为9x,7x,由题意得:
9x×7x=
×27×21 解得:x=
∴中央矩形的长为:9x=
宽为:7x=
∴左右边宽为:
- 
上下边宽为: 
- 
23、(1）不同类型的正确结论有：
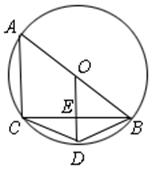①BE=CE；②BD=CD；③∠BED=90°；④∠BOD=∠A；⑤AC//OD；⑥AC⊥BC；
⑦
；⑧
；⑨△BOD是
等腰三角形；⑩
；等等。
(2) ①答：α与β之间的关系式为：
(1分)
证明: (略) (4分)
说明：如得出α与β之间的关系式为：
或α>β且证明
正确也对。
六、24、解：假设圆心在O处，连接OB，OD，过O作OK⊥AB于K，交CD于K，
交圆O于G点。设圆O的半径为r，则：
（r-2.4）2+3.62=r2
解得:r=3.9
∴OK=3.9-2.4=1.5米
当CD=3米时,HD=1.5米,则
OH2=3.92-1.52
OH=3.6
∴ HK=OH-OK=3.6-1.5=2.1米＞2米
∴此货船能顺利通过这座拱形桥.
25、．解：（1）所画⊙P如图所示，由图可知⊙P的半径为
，而
．
点在⊙P上．·········································· 3分
（2）
①
直线向上平移1个单位经过点，且经过点
，
，
，
．
．
则∠PDG=90°，
．直线与
相切．
（另法参照评分）……………………..7分
②
，
，
．
．
，
．
直线与劣弧围成的图形的面积为
． ……10分