初三数学下学期第一次月考试卷

一、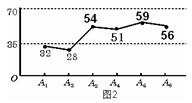填空题（每题3分，共30分）　　　　　　　　　　　　　　　　　

1、因式分解：　　　　　　　  .

2、103000用科学记数法可表示为______________。

6题图

3、函数中，自变量x的取值范围是______________。

4、某校初三（2）班想举办班徽设计比赛，全班50名同学，计划每位同学交设计方案一份，拟评选出10份为一等奖，那么该班某位同学获一等奖的概率为______________。

5、针对药品市场价格不规范的现象，药监部门对部分药品的价格进行了调整，已知某药品原价为a元，经过调整后，药价降低了60%，则该药品调整后的价格为______________元。

6、图2是一组数据的折线统计图，这组数据的极差是　　　　　 ，平均数约是　　　　 .（保留到整数位）

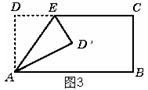
7、将矩形ABCD沿AE折叠，得到如图3所示的图形，已知∠CED^。=60°，则∠EAD =_______

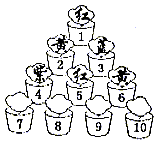
8、 把编号为1，2，3，4，…的若干盆花按下图所示摆放，花盆中的花按红、黄、蓝、紫的颜色依次循环排列，则第8行从左边数第6盆花的颜色为______________色。

7题图

　　　　

8题图

9题图

　　　 ……

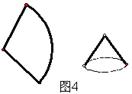
9、用一张面积为8πcm的扇形纸张卷成一个如图4 所示的圆锥，已知圆锥的母线是底面半径的两倍，则圆锥底面半径是___________.

10．已知△ABC的三边长分别为6cm、8cm、10cm，则这个三角形的外接圆的面积为__________cm²。（结果用含π的代数式表示）

二、选择题（每小题3分共18分）

11、一名同学所做的 5 道练习题： ① ；② ；③ ;　④ ；⑤ ；他做对的题数是（　　　　）

　A.  0　　　 B.　 1　　　 C.　 2　　　D.　 3

12、同时抛掷两枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，下列事件中是不可能事件的是（　　）

A. 点数之和为12　　　　  　　B. 点数之和小于3

 C. 点数之和大于4且小于8　　 D. 点数之和为13

 13. 已知，则m+n的值为（　　）

　　A. 　　　　　　　　B. 　　　　　C. 3　　　　　　　　　　 D. 不确定

　14、如图，C是⊙O上一点，O是圆心，若的度数为（　　）

　　A. 　　　　　　　 B. 　　　　 C. 　　　　　　　D. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

16题图

15题图

14题图

　　 　　　

 

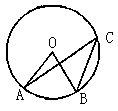
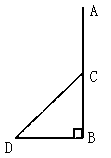
 15、如图，电线杆AB的中点C处有一标志物，在地面D点处测得标志物的仰角为45^o，若点D到电线杆底部点B的距离为a，则电线杆AB的长可表示为（　　）

　　A. a　　　　　　　　　　　　　　B. 2a　　　　　　 　　 C. a　　　　　　　　　　D.

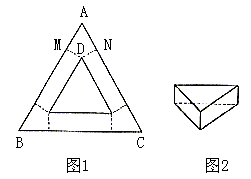
 16. 用一块等边三角形的硬纸片（如图1）做一个底面为等边三角形且高相等的无盖的盒子（边缝忽略不计，如图2），在的每个顶点处各需剪掉一个四边形，其中四边形AMDN中，MDN的度数为（　　）

　　A. 　　　　　　　　　　B. 　　　　　　　C. 　　　　　　　D.

三、解答题：

17、计算：　 （本题为5分）

18、（本小题满分7分）

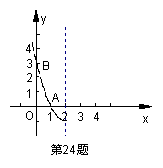已知抛物线的对称轴是经过点（2，0）且与y轴平行的直线，抛物线与x轴相交于点A（1，0），与y轴相交于点B（0，3），其在对称轴左侧的图像如图所示。

⑴ 求抛物线所对应的函数关系式，并写出抛物线的顶点坐标。

⑵ 画出抛物线在对称轴右侧的图像，并根据图像，写出当x为何值时，y<0。

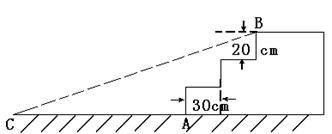19．（本题7分）如图，某公园入口处原有三级台阶，每级台阶高为20 cm,，深为30 cm，为方便残疾人士，拟将台阶改成斜坡，高台阶的起点为A，斜坡的起始点为C（如图所示），现将斜坡的坡角∠BCA设计为12°，那么斜坡起点C应离A点多远？

（精确到1 cm，sin12°=0.208，cos12°=0.978，tan12°=0.213）

20．某校七年级在学校团委的组织下，围绕“八荣八耻”开展了一次知识竞赛活动，

竞赛规则：每班代表队都必须回答27道题，答对一题得5分，答错或不答都倒扣1分。 

（1）在比赛到第18题结束时，（3）班代表队得分为78分，这时（3）班答对了多少道题？（7分）

（2）比赛规定，只有得分超过100分（含100分）时才能获奖。在第（1）小题的条件下，（3）班代表队在后面的比赛中至少还要答对多少题才有可能获奖？请简要说明理由。

21、（本小题满分8分）

如图，⊙O的半径是，圆心与坐标原点重合，在直角坐标系中，把横坐标、纵坐标都是整数的点称为格点。

⑴　   写出⊙O上所有格点的坐标：

___________________________________________________。

⑵ 设为经过⊙O上任意两个格点的直线。

① 满足条件的直线共有多少条？

② 求直线同时经过第一、二、四象限的概率。

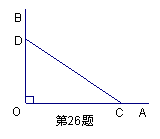
22．（本题为2分+2分+5分）如图，，点C、D分别在OA、OB上。

⑴ 尺规作图（不写作法，保留作图痕迹）：作的平分线OP；作线段CD的垂直平分线EF，分别与CD、OP相交于E、F；连结OE、CF、DF。

⑵ 在所画图中，

① 线段OE与CD之间有怎样的数量关系：_____________。

② 求证：△CDE为等腰直角三角形。

23．（本题满分为9分）某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试，考分都以同一标准划分成“不及格”、“及格”、“优秀”三个等级，为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考试考分等级，所绘制的统计图如图所示，试结合图形信息回答下列问题：

（1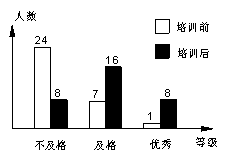）　  这32名学生培训前考分的中位数所在的等级是　　　 ，培训后考分的中位数所在的等级是　　　　．

（2）　　这32名学生经过培训，考分等级

“不合格”的百分比由　　  下降到　　　　  ．

（3）估计该校整个初二年级中，培训后考分

等级为“合格”与“优秀”的学生共有　　　　名．

（4）你认为上述估计合理吗？理由是什么？

答：　　　　　　  ，理由　　　　　　　　　　　　　　 　　　　　　 ．

五、探究题（每题10分，共20分）

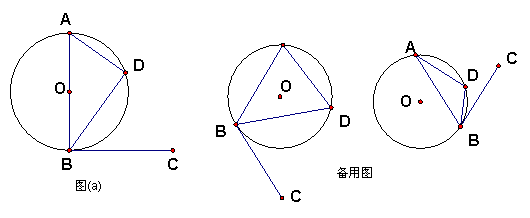
24. 如图(a)，已知AB是⊙O的直径，CB是⊙O的切线，B为切点，D是⊙O上一点(不A、B重合）.

（1）　  求证：∠DAB =∠DBC；

（2）　  若AB不是⊙O的直径，其它条件不变，(1)中的结论还成立吗？若成立

则给出你的证明；若不成立，请说明理由.

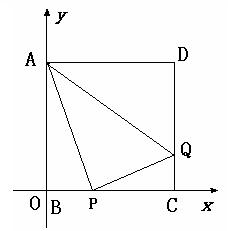
25. 如图所示，在平面直角坐标系中，正方形ABCD的边长为4，点Ｂ在系原点上，

P是BC上一动点，QP⊥AP交DC于Q，设PB=x，△ADQ的面积为y.

（1）求y与x之间的函数关系式，并写出自变量x的取值范围.

（2）（1）中函数若是一次函数，求出直线与两坐标轴围成的三角形面积，若是二

次函数，请利用配方法求出抛物线的对称轴和顶点坐标.

（3）点P是否存在这样的位置，使△APB的面积是△ADQ的面积的，若存在，

求出点P的坐标，若不存在，请说明理由.

 

24．（1）由题意，得c=3，a+b+3=0，，即　 2分（仅列出一个关系式，得1分）

解方程组，得

∴抛物线所对应的函数关系式为，

抛物线的顶点坐标为·································································· 4分

（2）画图．······································································································ 5分

由图像得，当1<x<3时，y<0。···························································· 6分

25．（1）格点坐标为：、、、、

、、、·················································· 2分

（2）满足条件的直线共有28条 ·································································· 4分

（3）“直线同时经过第一、二、四象限”记为事件A，它的发生有4种可能，所有事件A发生的概率P(A)=，即直线同时经过第一、二、四象限的概率为．···················· 6分

26．（1）画出角平分线、线段的垂直平分线。············ 3分（仅画出一条得2分）

（2）① ··························································································· 4分

② 方法一：∵EF是线段CD的垂直平分线，

∴FC=FD ·································································································· 5分

∵△COD为直角三角形，E为CD的中点

∴

∴

设CD与OP相交于点G，

∵

∴································································ 6分

又CE=OE=EF，

∴，同理

∴，△CDF等腰为直角三角形。·································· 7分

方法二：过点F作FM⊥OA、FN⊥OB，垂足分别为M、N。····· 5分

∵OP是∠AOB的平分线，

∴FM=FN。

又EF是CD的垂直平分线，

∴FC=FD。

∴Rt△CFM≌Rt△DFN，∠CFM=∠DFN。······································ 6分

在四边形MFNO中，由∠AOB=∠FMO=∠FNO=90°，得∠MFN=90°

∴∠CFD=∠CFM+∠MFD=∠DFN+∠MFD=∠MFN=90°

∴△CDF为等腰直角三角形。··························································· 7分

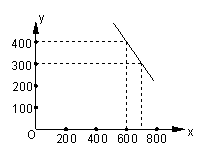
24. 某公司试销一种成本单价为500元/件的新产品，规定试销时的销售单价不低

于成本单价，又不高于800元/件，经试销调查发现销售量y（件）与销售单

价x（元/件）可近似看作一次函数的关系（如图所示）．

（1）根据图象，求一次函数的表达式；

（2）设公司获得的毛利润（毛利润=销售总价-成本总价）为S元．①试用销

售单价x表示毛利润S；②试问销售单价定为多少时，该公司获得最大毛利润？

最大毛利润是多少？此时的销售量是多少？