九年级数学相似教学质量检测试题
时间:120分钟 满分150分 得分:
一、精心选一选(下列各小题的四个选项中,有且只有一个是符合题意的,把你认为符合题意的答案代号填入答题表中,每小题3分,共39分)
1.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是( )A.19 B.17 C.24 D.21
2.下列说法不正确的是( )
 A.所有的矩形是相似的 B.含
A.所有的矩形是相似的 B.含![]() 直角三角形与含
直角三角形与含![]() 角的直角三角形是相似的
角的直角三角形是相似的
C.所有边数相等的正多边形是相似的 D.所有的等边三角形都是相似的
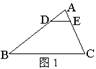
3.如图1,![]() ∽
∽![]() ,若
,若![]() ,则
,则![]() 与
与![]() 的
的
 相似比是( )A.1:2 B.1:3 C.2:3 D.3:2
相似比是( )A.1:2 B.1:3 C.2:3 D.3:2
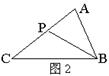
4.如图2,点P是![]() 的边AC上一点,连结BP,以下条件中,不能判定
的边AC上一点,连结BP,以下条件中,不能判定
![]() ∽
∽![]() 的是( )
的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
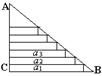
 5.如图3,小正方形的边长均为1,则图中三角形(阴影部分)与
5.如图3,小正方形的边长均为1,则图中三角形(阴影部分)与![]() 相似的是( )
相似的是( )
 |
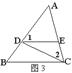
6.如图,D、E分别在边AB、AC上,且![]() ,则图中相似三角形有( )
,则图中相似三角形有( )
 A.1对 B.2对 C.3对 D.4对
A.1对 B.2对 C.3对 D.4对
 7.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的的矩形彩条,如图,在
7.某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的的矩形彩条,如图,在![]() 中,
中,![]() ,仿效裁下宽为
,仿效裁下宽为![]() 的矩形纸条
的矩形纸条![]() ,……,若使得裁得的矩形纸条的长都不小于
,……,若使得裁得的矩形纸条的长都不小于![]() ,则每张直角三角形彩纸能裁成的矩形纸条的总数是( )
,则每张直角三角形彩纸能裁成的矩形纸条的总数是( )
A.24 B.25 C.26 D.27
8.按下列方法把![]() 的三边缩小为原来的
的三边缩小为原来的![]() ,如图,任取一点O,连结
,如图,任取一点O,连结![]() 并取它们的中点
并取它们的中点![]() 得
得![]() ,则下列说法正确的个数是(
)
,则下列说法正确的个数是(
)
①![]() 与
与![]() 是位似图形;②
是位似图形;②![]() 与
与![]() 相似图形;③
相似图形;③![]() 与
与![]() 的周长比为
的周长比为![]() ;④
;④![]() 与
与![]() 的面积比为
的面积比为![]() A.1 B.2
C.3 D.4
A.1 B.2
C.3 D.4
 9.(2007绵阳市)如图,在正方形ABCD的外侧,作等边△ADE,BE、CE分别交AD于G、H,设△CDH、△GHE的面积分别为S1、S2,则( )
9.(2007绵阳市)如图,在正方形ABCD的外侧,作等边△ADE,BE、CE分别交AD于G、H,设△CDH、△GHE的面积分别为S1、S2,则( )
 A.3S1 =
2S2 B.2S1
= 3S2 C.2S1 =
A.3S1 =
2S2 B.2S1
= 3S2 C.2S1 =![]() S2 D.
S2 D.![]() S1 = 2S2
S1 = 2S2
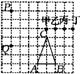
10.(2007成都市)如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为![]() ,那么大“鱼”上对应“顶点”的坐标为( )
,那么大“鱼”上对应“顶点”的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.(2007安徽芜湖市)如图, 在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3、AE=4,则CH的长是 ( )
A. 1 B. 2 C. 3 D.4
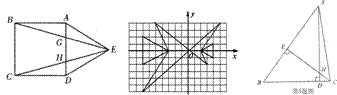
12.(2007山东烟台)如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使![]() ∽
∽![]() ,则点
,则点![]() 应是甲、乙、丙、丁四点中的( )
应是甲、乙、丙、丁四点中的( )
A.甲 B.乙 C.丙 D.丁
13.(2007浙江宁波)如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )
(A)24m (B)22m (C)20 m (D)18 m
二、细心填一填(每题3分,共27分)
14.如图,身高为![]() 的小明AB站在河边的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD的倒影为
的小明AB站在河边的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD的倒影为![]() 在一条视线上,已知河BD的宽度为
在一条视线上,已知河BD的宽度为![]() ,则树CD的高为 。
,则树CD的高为 。
15.如图,测量小玻璃管口径的量具ABC,AB的长为![]() ,AC被分为50等份,如果小玻璃管口DE正好对着量具上30等份处,(
,AC被分为50等份,如果小玻璃管口DE正好对着量具上30等份处,(![]() ),那么小玻璃管口径DE的长为
),那么小玻璃管口径DE的长为
16.(2007绵阳市)如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点O为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1∶2,则线段AC的中点P变换后对应的点的坐标为 .
17.(2007福建厦门)如图,在平行四边形ABCD中,AF交DC于E,交BC的延长线于F,∠DAE=20°,∠AED=90°,则∠B=
度;若![]() ,AD=4厘米,则CF=
厘米.
,AD=4厘米,则CF=
厘米.
18.某课外活动小组的同学在研究某植物标本时,测得叶片①最大宽度是![]() ,最大长度是
,最大长度是![]() ;②最大宽度是
;②最大宽度是![]() ,最大长度是
,最大长度是![]() ;③最大宽度是
;③最大宽度是![]() 。请你用所学的知识估算叶片③的完整叶子的最大长度,结果约为
。请你用所学的知识估算叶片③的完整叶子的最大长度,结果约为 ![]() 。
。
19.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为 cm.

![]() 20.如图,平行四边形ABCD中,AE∶EB=1∶2,BF∥DE,如果
20.如图,平行四边形ABCD中,AE∶EB=1∶2,BF∥DE,如果![]() ,则四边形FDGH的面积为
,则四边形FDGH的面积为
21.(2007湖北荆门)圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(如图所示).已知桌面的直径1.2米,桌面距离地面1米.若灯泡距离地面![]() 米,则地面上阴影部分的面积为
米,则地面上阴影部分的面积为 ![]()
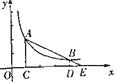 22.(2007眉山市)如图,A、B是反比例函数y=
22.(2007眉山市)如图,A、B是反比例函数y=![]() 的图象上的两点.AC、BD都垂直于x轴,垂足分别为C、D.AB的延长线交x轴于点E.若C、D的坐标分别为(1,0)、(4,0),则ΔBDE的面积与ΔACE的面积的比值是
的图象上的两点.AC、BD都垂直于x轴,垂足分别为C、D.AB的延长线交x轴于点E.若C、D的坐标分别为(1,0)、(4,0),则ΔBDE的面积与ΔACE的面积的比值是
三、解答题:(共84分◆认真解答,一定要细心哟!相信你是最棒的!)
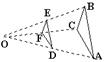
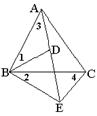 1.(12分)如图,点
1.(12分)如图,点![]() 是
是![]() 内一点,点
内一点,点![]() 是
是![]() 外的一点,且
外的一点,且![]() ,图中有与
,图中有与![]() 相等的角吗?如果有,请找出来,并说明理由。
相等的角吗?如果有,请找出来,并说明理由。
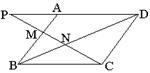 2.(12分)如图,
2.(12分)如图,![]()
![]() 中,
中,![]() 是
是![]() 上的一点,连结
上的一点,连结![]() 并延长交
并延长交![]() 的延长线于
的延长线于![]() ,交对角线
,交对角线![]() 于
于![]() ,求证:
,求证:![]()
3.(12分)(2007福建泉州市)如图,在梯形ABCD中,AD∥BC,∠B=∠ACD
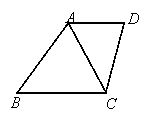 ⑴请再写出图中另外一对相等的角;
⑴请再写出图中另外一对相等的角;
⑵若AC=6,BC=9,试求梯形ABCD的中位线的长度。
4.(12分)(2007山东潍坊)如图(1),线段![]() 过圆心
过圆心![]() ,交⊙
,交⊙![]() 于
于![]() 、
、![]() 两点,PC切⊙
两点,PC切⊙![]() 于点
于点![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() 。(1)写出图(1)中所有相等的角(除直角外),并给出证明;(2)若图(1)中的切线
。(1)写出图(1)中所有相等的角(除直角外),并给出证明;(2)若图(1)中的切线![]() 变为图(2)中割线
变为图(2)中割线![]() 的情形,
的情形,![]() 与⊙
与⊙![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,写出图(2)中相等的角(写出三组即可,除直角外);(3)在图(2)中,证明:
,写出图(2)中相等的角(写出三组即可,除直角外);(3)在图(2)中,证明:![]()
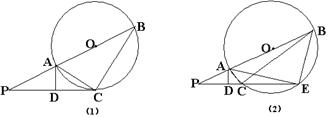 |
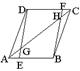
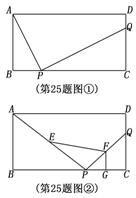 5.(12分)(2007福建三明市)已知:如图①,②,在矩形
5.(12分)(2007福建三明市)已知:如图①,②,在矩形![]() 中,
中,![]() =4,
=4,![]() =8,
=8,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点.(1)如图①,若
上的点.(1)如图①,若![]() ,
,![]() =2,求
=2,求![]() 的长;(2)如图②,若
的长;(2)如图②,若![]() ,且
,且![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,求四边形
的中点,求四边形![]() 的面积.
的面积.
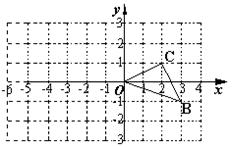 6.(12分)(2006淮安)如图,已知
6.(12分)(2006淮安)如图,已知![]() 是坐标原点,
是坐标原点,![]() 两点的坐标分别为(3,
两点的坐标分别为(3,![]() )、(2,1)。(1)以
)、(2,1)。(1)以![]() 点为位似中心在
点为位似中心在![]() 轴的左侧将
轴的左侧将![]() 放大两倍,(即新图与原图的相似比为2),画出图形;(2)分别写出
放大两倍,(即新图与原图的相似比为2),画出图形;(2)分别写出![]() 、
、![]() 两点的对应
两点的对应![]() 、
、![]() 的坐标;(3)如果
的坐标;(3)如果![]() 内部一点
内部一点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),写出
),写出![]() 的对应点
的对应点![]() 的坐标。
的坐标。
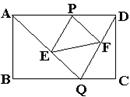 7.(12分)如图,已知矩形
7.(12分)如图,已知矩形![]() 的边长
的边长![]() ,点
,点![]() 是
是![]() 上一动点(异于
上一动点(异于![]() 、
、![]() ),
),![]() 是
是![]() 边上的任意一点,连接
边上的任意一点,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于
于![]() 。(1)求证:
。(1)求证:![]() ∽
∽![]() ;(2)设
;(2)设![]() 的长为
的长为![]() ,试求
,试求![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式;(3)当Q在何处时,
的函数关系式;(3)当Q在何处时,![]() 的周长最小。
的周长最小。