第一学期九年级期末数学练习卷(二)
一、选择题(每题2分,共24分)
1. 下列根式中,与![]() 不是同类二次根式的是 ( )
不是同类二次根式的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 抛物线![]() 与
与![]() 轴的交点坐标是( )
轴的交点坐标是( )
A.(2,0) B.(![]() 2,0) C.(0,
2,0) C.(0,![]() 4,) D.(0,4)
4,) D.(0,4)
3. 一元二次方程![]() 的解是 ( )
的解是 ( )
A.![]() B、
B、![]() C、
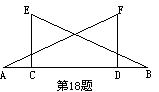
C、![]() D、
D、![]()
4. 两圆相切,圆心距为9 cm,已知其中一圆半径为5 cm,另一圆半径为( ).
A.14 B.5 C.4 D.14或4
5. 若式子![]() 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A. x≥-2 B.x>1 C. x>-2且x≠1 D. x≥-2且x≠1
6.若圆锥侧面积是底面积的2倍,则这个圆锥的侧面展开图的圆心角是 ( )
A.120° B.135° C.150° D.180°
7. 矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对角线平分一组对角
8. 国家统计局发布的统计公报显示:2001到2005年,我国GDP增长率分别为8.3%,9.1%,10.0%,10.1%,9.9%.经济学家评论说:这五年的年度GDP增长率之间相当平稳.从统计学的角度看,“增长率之间相当平稳”,说明这组数据的( )较小.
A.中位数 B.标准差 C.平均数 D. 众数
 9.在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成三角形,又能拼成平行四边形和梯形的可能是( )
9.在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成三角形,又能拼成平行四边形和梯形的可能是( )
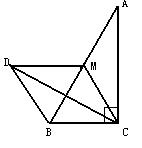
10. 如图,点A、B、C在⊙O上,AO∥BC,∠OAC=15°,则∠AOB的度数是( )
 A.15° B.20° C.30° D.40°
A.15° B.20° C.30° D.40°
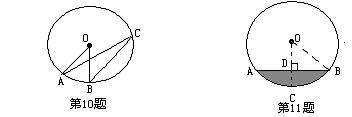
11. 某小区一处圆柱形输水管道的圆形截面如图所示.若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度CD为4cm.则这个圆形截面的半径是( )
A.20 B. 18 C. 12 D.10
12. 造一个池底为正方形,深度为2.5的长方形无盖蓄水池,池壁的造价为120元/m2, 池底的造价为240元/m2,总造价为8640元,求池底的边长. 若设池底的边长为 ![]()
![]() .根据题意列出方程是:( )
.根据题意列出方程是:( )
A. 240![]() B. 240
B. 240![]()
C. 480![]() D. 480
D. 480![]()
二、填空题(每题2分,共16分)
13. 计算:![]() = ;
= ;![]() = .
= .
14. 若一组数据1,2,3,x的极差为6,则x的值是 .
15.请你写出一个根为![]() ,另一根满足
,另一根满足![]() 的一个一元二次方程: .
的一个一元二次方程: .
16.一件产品原来每件的成本是100元,由于连续两次降低成本,现在的成本是81元,则平均每次降低成本是 % .
17.请你写出一个开口向上,对称轴为直线x=2的抛物线: .
18. 如图,已知AD=BC、EC⊥AB、DF⊥AB,C、D为垂足,要使ΔAFD≌ΔBEC,还需添加一个条件.若以“ASA”为依据,则添加的条件是 .
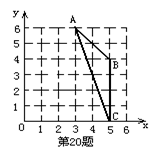
19. 如图,将一把宽2cm的直尺如图放置,直尺经过圆心O且与⊙O分别交于点A、B、C、D.若AB=8cm,则CD = cm.
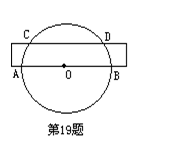
20. 如图,△ABC的顶点在格点上,则△ABC外接圆的圆心坐标是 .
三、解答题
21.(本题4分) 22. (本题4分)
计算:![]() 解方程:
解方程:![]()
23. (本题8分)
已知二次函数![]() .
.
(1)在所给的直角坐标系中,画出该函数的图象;
(2)写出该函数图象的对称轴、顶点坐标和图象与![]() 轴的交点坐标;
轴的交点坐标;
 (3)观察函数图象,写出
(3)观察函数图象,写出![]() 时,x的取值范围.
时,x的取值范围.
24. (本题8分)
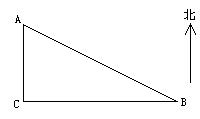
某海关缉私艇在C处发现在正北方向30km的A处有一艘可疑船只,测得它正以75km/h的速度向南偏东方向航行.缉私艇随即以60km/h的速度向正东方向航行,并在B处拦截,问缉私艇从C处到B处需航行多长时间?
25. (本题8分)
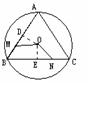
在Rt△ABC中,∠C=90º,∠A=30º ,CM为斜边AB的中线,将△ACM沿CM折叠至如图所示位置,连接BD.
|
(2)若BC=2,求四边形BCMD的面积.
26. (本题9分)
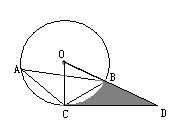
如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°.
(1) 试判断直线CD与⊙O的位置关系,并说明理由.
(2) 若⊙O的半径长为1,求由弧BC、线段CD和BD所围成的阴影部分面积(结果保留和根号).
27. (本题9分)
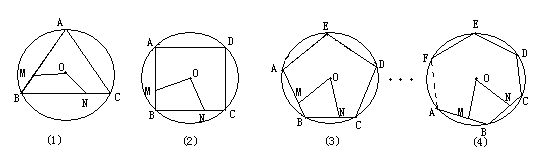
如图(1)、(2)、(3)…(n),M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.
①求图(1)中∠MON的度数;
②图(2)中∠MON的度数是 ,图(n)中∠MON的度数是 ;
③试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
28. (本题10分)
如图,四边形ABCD为矩形,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于点P,连接MP.已知动点运动了x秒.
(1) 请直接写出PN的长;(用含x的代数式表示)
(2) 若0≤x≤1,试求MPA的面积S与时间x秒的函数关系式及S的最大值.
(3) 若0≤x≤3,MPA能否为一个等腰三角形?若能,试求出所有x的对应值;若不能,试说明理由.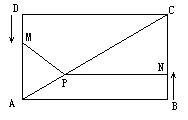
2007~2008学年度第一学期九年级期末数学练习卷(二)
参考答案
一、选择题(每题2分,共24分)
1. B 2. D 3. C 4. C 5. D 6. D 7. B8. B 9. C 10. C 11. D 12. A
二、填空题(每题2分,共16分)
13.![]() ,
,![]() ; 14. 7 ; 15.
; 14. 7 ; 15. ![]() ; 16. 10% ; 17.
; 16. 10% ; 17.![]() .;
.;
18. CE=DF; 19.![]() ; 20.(1,2).
; 20.(1,2).
三、解答题
21.(本题4分) 22. (本题4分)
解:原式=![]() ----4分
解:
----4分
解:![]() ----2分
----2分
=![]() ---------4 分
---------4 分
![]() ----4分
----4分
23. (本题8分)
解:(1)略.-----2分
(2)![]()
![]() ;
;
![]()
![]() .-----6- 分
.-----6- 分
(3)![]() -------------------8分
-------------------8分
24. (本题8分)
由题意得方程:![]()
解得:x=![]() (小时)---------------7分
(小时)---------------7分
答:缉私艇从C处到B处需航行![]() 小时.-------8分
小时.-------8分
25. (本题8分)
证明:(1)在Rt△ABC中,因为CM为斜边AB的中线.
所以,BM=CM.
又因为∠A=30 º,所以,∠ABC=60º.
所以BM=CM=BC
即△BCM为正三角形.------4分
(2)因为∠DMC=∠AMC=120º.
所以,∠DMB=60º,
所以,DM∥BC,又因为DM=AM=BM=BC.
所以四边形BCMD为平行四边形.------6分
所以![]()
![]() .--------8分
.--------8分
26. (本题9分)
解:(1)CD与⊙O相切.-----2分
∵∠BOC=2∠A=60°,又∵OB=OC
∴∠BCO=60°,∠BCD =30°
∴∠DCO=90°,即OC⊥CD,
点C在圆上,∴CD与⊙O相切.---------5分
(2)在Rt△OCD中,∠BOC=60°,OC=1.
∴CD=![]() ,
,![]() .
. ![]() .
.
∴阴影部分面积=![]() -----------9分
-----------9分
27. (本题9分)
 解:①过O点分别作OD⊥AB,OE⊥BC.
解:①过O点分别作OD⊥AB,OE⊥BC.
在正△ABC中,BM=CN,∴EN=DM,OD=OE.
Rt△ODM≌OEN,∴∠DOM=∠NOE.
∴∠MON=∠DOE=120°.-----------4分
②∠MON=90°,∠MON=72°.------7分
③![]() ------------------9分
------------------9分
28. (本题10分)
解:(1)由△CNP∽△CBA可得PN=![]() ---2分
---2分
(2)S=![]() ----------------------5分
----------------------5分
![]() --------------------------7分
--------------------------7分
(3)当x=1,或![]() --------10分
--------10分