第二学期
九年级数学第二学期期中测试卷
| 题号 | 一 | 二 | 三 | 四 | 总分 | 评卷人 | 复核人 |
本试卷满分150分(前三大题100分,第四大题50分)考试时间120分钟。
| 得分 | 评卷人 |
|
|
![]() 一、本大题有10个小题,每小题3分,共30分。每小题给出的四个选项中只有一个是正确的,请将题后的代号填入题后的括弧内。
一、本大题有10个小题,每小题3分,共30分。每小题给出的四个选项中只有一个是正确的,请将题后的代号填入题后的括弧内。
1、在代数式3m+n, -2mn, p, 0, 中单项式的个数为 ( )
A、 5 B、4 C、3 D、 2
2、下列选项中不是正六棱柱三视图的是 ( )
 |
A
B
C
D![]()
![]()
3、若关于x的方程 - =0有增根,则m的值为 ( )
A、 3 B、 2 C、 1 D、 -1
![]() 4、函数y=√x-3中,自变量x的取值范围是
(
)
4、函数y=√x-3中,自变量x的取值范围是
(
)
A、x>3 B、x≥3 C、x>-3 D、x≥-3
5、1nm为十亿分之一米,而个体中红细胞的直径约为
0.m,那么人体中红细胞直径的纳米数用科学记数法表示为 ( )
A、7.7×103mm B、7.7×102mm
C、7.7×104mm D、以上都不对
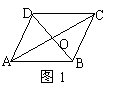 6、如图1,□ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是
(
)
6、如图1,□ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是
(
)
A、1< m <11 B、2< m <22
C、10< m <12 D、5< m <6
7、一组数据的方差为s2,将这组数据的每个数据
![]() 都乘以2,所得到的一组新数据的方差是
(
)
都乘以2,所得到的一组新数据的方差是
(
)
A、 S2 B、S2 C、2S2 D、4S2
8、若一个圆的内接正三角形、正方形、正六边形的边心距分别为r1,r2,r3,则
r1:r2:r3等于 ( )
![]()
![]()
![]()
![]() A、1:2:3 B、 √3 :√2:1 C、1:√2:√3 D、3:2:1
A、1:2:3 B、 √3 :√2:1 C、1:√2:√3 D、3:2:1
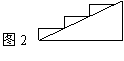
9、如图2,在高为2m,坡角为30°的楼梯上铺地毯,地毯的长度至少应计( )
![]()
![]() A、 4m B、 6m C、4√2m D、 2+2√3m
A、 4m B、 6m C、4√2m D、 2+2√3m
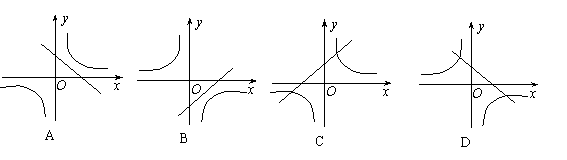
![]() 10在同一直角坐标系中,函数y=kx-k与y= (k≠0)的图象大致
( )
10在同一直角坐标系中,函数y=kx-k与y= (k≠0)的图象大致
( )
| 得分 | 评卷人 |
|
|
二、填空题:本大题共10个小题,每小题3分,共30分。把答案填在题中的横线上。
11、分解因式:x2+4x+4= .
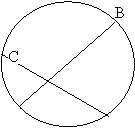
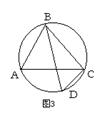
12、如图3,点A、B、C、D在圆周上,∠A =65°,则∠D = .
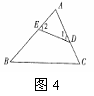
13、如图4,D、E两点分别在AC、AB上,且DE与BC不平行,请填上一个你认为合适的条件: ,使得△ADE∽△ABC.
14、若一个多边形的每个外角都等于30°,则这个多边形的内角和等于 .
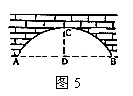
15、如图5,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为 .
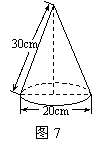
 16、如图6,AB是⊙O的直径,C是⊙O上一点,若AC:BC=4:3,AB=10cm,OD⊥BC于点D,则BD的长为
.
16、如图6,AB是⊙O的直径,C是⊙O上一点,若AC:BC=4:3,AB=10cm,OD⊥BC于点D,则BD的长为
.
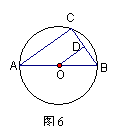
17、图7是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽的纸的面积
为 cm2(π取3.14).
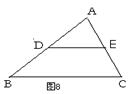
18、如图8,DE是△ABC的中位线,S△ADE = 3,则S△ABC = .
19、某种商品的价格标签已经看不清,售货员只知道某种商品的进价为800元,打七折售出后,仍可获利5%,你来帮助售货员重新填好价格标签应
为 元。
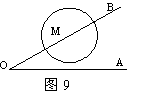
20、如图9,已知∠AOB = 30 ,M为OB边上一点,以M为圆心、2cm为半径作⊙M.若点M在OB边上运动,则当OM= cm时,⊙M与OA相切.
 |
| 得分 | 评卷人 |
|
|
三、解答题:本大题共5个小题,共40分。要写出必要的文字说明、证明过程及演算步骤。
![]()
![]()
![]() 21、计算:√8 +( )-1- 4cos45°-2÷ ×2(6分)
21、计算:√8 +( )-1- 4cos45°-2÷ ×2(6分)
![]() 22、已知双曲线y= 和直线y=kx+2相交于点A(
22、已知双曲线y= 和直线y=kx+2相交于点A(![]() ,
,![]() )和点B(
)和点B(![]() ,
,![]() ),且x12+x22=10,求
),且x12+x22=10,求![]() 的值.(8分)
的值.(8分)
23、如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?(8分)
 |
24、某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品50件。已知生产一件A种产品用甲种原料9千克,乙种原料3千克,生产一件B种产品,需要甲种原料4千克,乙种原料10千克。按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来。(9分)
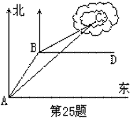
25、一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?(9分)
| 得分 | 评卷人 |
|
|
四、解答题:本大题共5个小题,共50分。要写出必要的文字说明、证明过程及演算步骤。
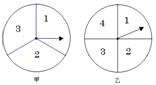 26、同时转动如图所示的甲、乙两个转盘,求两个转盘所转到的两个数字之和为奇数的概率(用树状图或列表法分析求解).(8分)
26、同时转动如图所示的甲、乙两个转盘,求两个转盘所转到的两个数字之和为奇数的概率(用树状图或列表法分析求解).(8分)
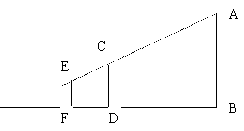 27、九年级(1)课外活动小组利用标杆测量学校旗杆的高度,标杆CD等于3m,标杆与旗杆的水平距离BD=15m,人的眼睛距地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m。求旗杆AB的高度。(8分)
27、九年级(1)课外活动小组利用标杆测量学校旗杆的高度,标杆CD等于3m,标杆与旗杆的水平距离BD=15m,人的眼睛距地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m。求旗杆AB的高度。(8分)
28、张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15立方米的无盖长方体运输箱,且此长方体运输箱底面的长比宽多2米。现在已知购买这种铁皮每平方米需要20元,问张大叔购回这张矩形铁皮共花多少元钱?(10分)
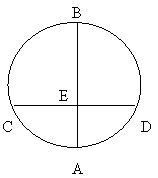
29、在一次数学实验探究课中,需要研究同一个圆中两条线段的关系问题,某同学完成了以下部分的记录,单位:cm(12分)
| 测 量 结果 | 第一次
| 第二次
V | 第三次
| |||||||||
| AE | 2.00 | 3.00 | 4.00 | |||||||||
| BE | 6.00 | 5.00 | 5.00 | |||||||||
| CE | 3.00 | 7.50 | 2.00 | |||||||||
| DE | 4.00 | 2.00 | 10.00 | |||||||||
| AE×BE | ||||||||||||
| CE×DE |
(1)请计算 AE×BE,CE×DE的值,并填入上表相应的位置。
(2)猜想对在同一个圆中,两条线段相交,被交点分成的两条线段的积有什么关系?并试着证明。
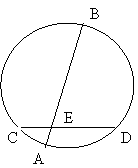
(3)利用上述结论,解决问题:AB为⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径R.
![]()
![]() 30、如图,△ABO的顶点A是双曲线y=
与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B,且S△ABO= (12分)
30、如图,△ABO的顶点A是双曲线y=
与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于点B,且S△ABO= (12分)
(1) 求两函数的解析式。
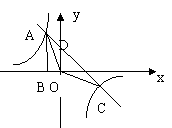 (2)若直线与双曲线相交于A、C两点,求交点A、C、D的坐标和△AOC的面积。
(2)若直线与双曲线相交于A、C两点,求交点A、C、D的坐标和△AOC的面积。