九年级数学(下)全册过关检测
（考试时间：120分钟；满分120分）
班级 姓名 得分
一．选择题(每小题3分,共30分,将正确答案的选项填在以下表格中)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1. 在△ABC中，A，B为锐角，且有
，则这个三角形是( )
A. 等腰三角形; B.直角三角形; C.钝角三角形; D. 锐角三角形
2.sin70°、cos70°、tan70°的大小关系是( )
A.sin70°>cos70°>tan70°; B. tan70°>cos70°>sin70°;
C. cos70°> sin70º> tan70°; D. tan70º > sin70º >cos70º
3.已知△ABC中，AD是高，AD=2，DB=2，CD=2
，则∠BAC= ( )
A. 1050 B. 150 C.1050或150 D. 600
4. 已知圆柱的侧面积是100πcm2，若圆柱底面半径为r（cm），高线长为h（cm），则h关于r的函数的图象大致是( )
5.直角坐标平面上将二次函数y＝-2(x－1)2－2的图象向左平移１个单位，再向上平移１个单位，则其顶点为( )
A.(0，0) B.(1，－2) C.(0，－1) D.(－2，1)
6.函数
的图象与
轴有交点，则
的取值范围是( )
A．
B．
C．
D．
7. 已知⊙O1与⊙O2内切，它们的半径分别为2和3，则这两圆的圆心距d满足( )
A、d=5 B、d=1 C、1<d<5 D、d>5
8.某工厂在抽查的100件产品中,有95件正品,5件是次品,从中任抽一件是次品的概率为( )
A.0.05 B. 0.5 C. 0.95 D.95
9.盒中装有5个大小相同的球，其中3个白球，2个红球，从中任意取两个球，恰好取到一个红球和一个白球的概率是( )
A. 
B．
C．
D.
10．直线
不经过第三象限，那么
+3的图象大致为( )
y
y
y
y
 |  | ||||
 | |||||
O x
O
x
O x
O x
A B C D
二.填空题(每小题3分,共30分,将正确答案填写在横线上)
1.在Rt⊿ABC中，∠C＝90°，BC＝10，AC＝4，则cosB= ,tanA= ；
2.等腰三角形的腰长为3，底边长为2，则底角的余弦值为 ；
3. 若∠A为锐角，且
，则∠A＝ ；
4抛物线
，若其顶点在轴上，则
．
5.已知二次函数
，则当 时，其最大值为0．
6.若一个圆锥的母线长为5cm,高为4cm,则圆锥的侧面展开图的面积为 .
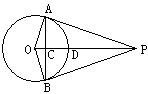7.如图，P是⊙O外一点，OP垂直于弦AB于点C，交
于点D，连结OA、OB、AP、BP。根据以上条件，写出三个正确结论（OA=OB除外）：
①
；②
;③
。
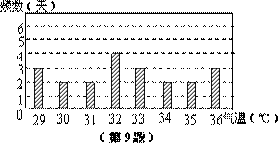8. 根据某市去年7月份中某21天的各天最高气温（℃）记录，制作了如图的统计图，由图中信息可知，记录的这些最高气温的众数是
℃，其中最高气温达到35℃以上（包括35℃）的天数有
天.
9.如果抛物线
和直线
都经过点P(2，6)，则
_______，
=_______，直线不经过第_______象限，抛物线不经过第_______象限．
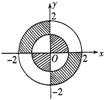
10.如图，是以直角坐标原点O为圆心的两个同心圆，则其阴影部分的面积之和为 ；(结果保留π)
三．解答题.（共60分,写出必要的步骤,直接写出答案不得分）
1. (8分)已知，如图，
，
，求
的余弦和正切，
的正弦和余切.
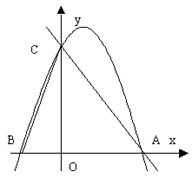
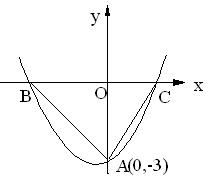
2.(10分)如图,二次函数y=ax2+bx+c的图象与x轴交于B,C两点,与y轴交于A点.
(1).根据图象确定a,b,c的符号;
(2)如果点A的坐标为(0,-3),∠ABC=450, ∠ACB=600,求这个二次函数的解析式.
3.(10分)某商人如果将进货价为8元的商品按每件10元出售，每天可销售100件，现采用提高售出价，减少进货量的办法增加利润，已知这种商品每涨价1元其销售量就要减少10件，问他将售出价定为多少元时，才能使每天所赚的利润最大？并求出最大利润．
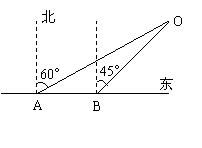4.(10分)如图，某船由西向东航行，在点A测得小岛O在北偏东60°，船行了10海里后到达点B，这时测得小岛O在北偏东45°。由于以小岛O为圆心16海里为半径的范围内有暗礁，如果该船不改变航向继续航行，有没有触礁的危险？通过计算说明。（供选用数据：
，
）
5．(10分)
如图，河对岸有铁塔AB，在C处测得塔顶A的仰角为30°，向塔前进14米到达D，在D处测得A的仰角为45°，求铁塔AB的高。
6.(12分)如图已知一交函数y=-2x+6的图象与x轴交于点A，与y轴交于点C；二次函数y=ax2+bx+c(a≠0)的图象过A、C两点，并且与x轴交于另一点B（B在负半轴上）。
（1）当S△ABC=4S△B0C时，求抛物线y=ax2+bx+c的解析式和此函数顶点坐标。
（2）以OA的长为直径作⊙M，试判定⊙M与直线AC的位置关系，并说明理由。
