第一学期九年级数学期中练习卷（一）
| 题 号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 总 分 |
| 得 分 |
|
|
|
|
|
|
|
|
|
一、选择题(每小题2分，共24分)
1．式子在实数范围内有意义，x的取值范围是（ ）.
A. x ＞ 1 B. x ≥ 1 C. x ＞ －1 D. x ≤ 1
2．一元二次方程x2－1＝0的根为（ ）．
A. x＝1 B. x＝－1 C. x1＝1，x2＝－1 D. x1＝0，x2＝1
3．具备下列条件的四边形中，不一定是平行四边形的是（ ）.
A．两组对边分别相等 B．两组对边分别平行
C．两条对角线相等 D．两条对角线互相平分
4．顺次连接等腰梯形各边中点所得的四边形必定是（ ）.
Ａ．矩形 Ｂ．等腰梯形 Ｃ．正方形 Ｄ．菱形
5. 下列计算正确的是（ ）.
A．3－2＝9 B．＋＝
C．（1＋）（1－）＝1 D．＝2
6．2007年4月17日国家测绘局首次公布了我国十座名山的海拔
高度（如图所示），这组数据的极差是（ ）.
A．3079.3米
B．1300.2米
C．4379.5米
D．1779.1米
7. 数据2，4，3，6，
的平均数是5，则这个样本的方差是（ ）.
A．8 B．5 C．2 D．3
8. 
，那么
的值为（ ）.
A. 1
B. －1 C.
D.
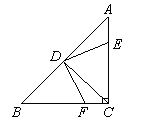9．如图，在△ABC中，∠C＝90°，∠A＝∠B，CD是中线，点E、F分别在边AC和BC上，且AE＝CF，则图中全等三角形有（ ）.
A．4对 B．3对 C．2对 D．1对
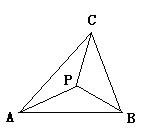10．如图，点P是△ABC内的一点，若PB＝PC，则（ ）.
A．点P在∠ABC的平分线上
B．点P在∠ACB的平分线上
C．点P在边AB的垂直平分线上
D．点P在边BC的垂直平分线上
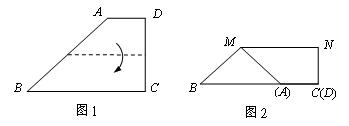11. 如图1，梯形ABCD中， ÐC＝ÐD＝90°， AD＝6，BC＝18．若将AD叠合在BC上，出现折痕MN，如图2所示，则MN的长度为（ ）.
A．9 B．12
C．15 D．21
12．
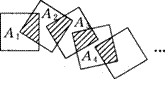将n个边长都为l cm的正方形按如图所示的方法摆放，点A1，A2，……，A n分别为正方形的中心，则n个这样的正方形重叠部分(阴影部分)的面积之和为（ ）.
A．
cm2
B．n cm2
Ｃ．
cm2 D．
cm2
二、填空题(每小题2分，共12分)
13. 方程x（x－3）＝3－x的解为_ __________ .
14．把方程x2＋6x－5＝0配方，得（x＋a）2＝b的形式，则所得的方程为 .
15．梯形的上底长为5cm，中位线长为8 cm，下底长为 cm .
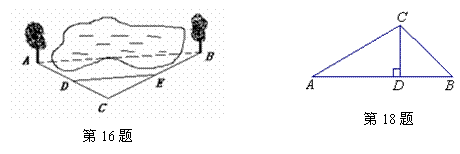
16. 如图，池塘边有两棵小树A、B，现测得线段AC和BC的中点分别为点D、E，且DE＝18．4 m，则这两棵小树之间的距离为 m．
17．已知菱形的边长为10 cm，一条对角线的长为12 cm，则菱形的面积为
cm
．
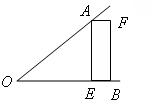
18．如图，在△ABC中，∠B＝45°，∠ACB＝105°，CD⊥AB于点D，若AC＝8，则BC＝ ．
三、计算与求解（每小题5分,共20分）
19．计算：＋(－1)3－2×
20.计算： （
＋1）0－＋∣－∣．
21．解方程：（x＋2）2＝x＋2.
22．解方程：x2 —1＝2x .
四、（本题4分）
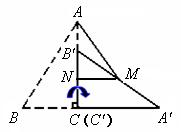
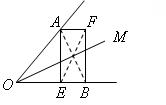
23．如图，已知∠AOB，OA＝OB，点E在OB边上，四边形AEBF是矩形．请你只用无刻度的直尺在图中画出∠AOB的平分线（请保留画图痕迹）．
五、（每小题7分，共14分）
24．两组邻边分别相等的四边形我们称它为筝形．
如图，在筝形ABCD中，AB＝AD，BC=DC，AC与BD相交于点O.
（1）下列判断正确的有
（填序号）.
①AC、BD互相垂直 ②AC、BD互相平分
③AC平分∠BAD、∠BCD ④BD平分∠ABD、∠ADC
（2）求证：①△ABC≌△ADC.
25．某农场去年种植了10亩地的南瓜，亩产量为2000
，根据市场需要，今年该农场扩大了种植面积，并且全部种植了高产的新品种南瓜，已知南瓜种植面积的增长率是亩产量的增长率的2倍，今年南瓜的总产量为60 000kg，求南瓜亩产量的增长率．
六、（本题7分）
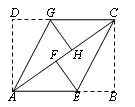
26． 如图，将Rt△ABC绕点C按顺时针方向旋转90°到△A’B’C’的位置，已知斜边AB＝10cm，BC＝6 cm，设A’B’的中点为M，B’C’的中点为N，连接AM，MN．
（1）△AMN是何种三角形？说明你的理由；
（2）求AM的长．
七、（本题9分）
27．
如图，ABCD是矩形纸片，翻折∠B、∠D，使BC、AD恰好落在AC上．设F、H分别是B、D落在AC上的两点，E、G分别是折痕CE、AG与AB、CD的交点．
(1) 求证：四边形AECG是平行四边形；
(2) 若AB＝4cm，BC＝3cm，求线段EF的长；
八、（本题10分）
28.在△ABC中，∠ACB=90°，AC = BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E；
（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE＝AD＋BE；
（2）当直线MN绕点C旋转到图2的位置时，写出DE、AD、BE具有的等量关系（不要证明）；
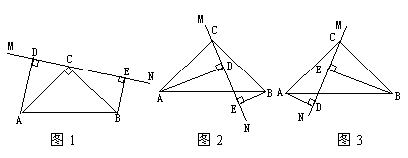（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明.
2007/2008学年度第一学期九年级数学期中练习卷
参考答案及评分标准
一、选择题（每小题2分，共24分）
1. B 2. C 3. C 4.D 5. D 6. D 7. A 8. A 9. B 10. D 11. B 12. C
二、填空题（每小题2分，共12分）
13. x1＝－1，x2＝3 14.（x＋3）2＝14 15.11 16.36.8 17. 96 18. 4
三、（每小题5分，共20分）
19.解：原式＝2－1－………………………………………………3分
＝－1. ……………………………………………………5分
20. 解：原式＝1－3＋………………………………………………3分
＝1－2.………………………………………………………5分
21. 解：x1＝－1，x2＝－2 …………………………………（解错一个扣2分）
22. 解：x1＝＋1，x2＝－＋1 …………………（解错一个扣2分）
四、（本题4分）
23．
解：
射线OM即为所求. …………………（不写结论扣1分）
五、（每小题7分，共14分）
24．（1） ①③………………………………………3分
（2）证明：在
和
中，
，
，
，·································································· 6分
．·························································································· 7分
25. 解：设南瓜亩产量的增长率为
，则种植面积的增长率为
．······························· 1分
根据题意，得
10（1＋2x）·2000（1＋x）＝60 000．···································································· 4分
解这个方程，得
，
（不合题意，舍去）．······································· 6分
答：南瓜亩产量的增长率为
．………………………………………………………7分
六、（本题7分）
26. 解：△AMN是直角三角形．………………………1分
（1）在△A′B′C′中，Ｍ、N分别是A′B′、B′C′的中点，
∴MN∥A′C′, ……………………………………2分
∵A′C′⊥B′C′， ∴MN⊥B′C′ ．
∴△AMN是直角三角形．………………………3分
（2）∵A′C′=AC=＝＝8（cm），
∴MN=
A′C′=4（cm）．………………………4分
而B′ N=C′N＝B′C′＝BC=３（cm），
∴AN=AC－C′N=8－3=5（cm）.……………………………………………………5分
∴AM=
（cm）.………………………………7分
七、（本题10分）
27．（1）证明：根据题意和图形的对称性，
∠ACE＝∠ACB，∠CAG＝∠CAD，
∵四边形ABCD是矩形，∴∠ACB＝∠CAD.
∴∠ACE＝∠CAG. ……………………………………………………………2分
∴CE∥AG. ……………………………………………………………3分
∵CG∥AE，……………………………………………………………4分
∴四边形AECG是平行四边形. ……………………………………5分
（2）解：设EF为x，则根据题意BE＝x，AE＝4－x.
∵AB＝4cm，BC＝3cm，∴AC＝5cm，BC＝CF＝3cm，AF＝2cm.
在Rt△AEF中，AE2＝AF2＋EF2.即（4－x）2＝22＋x2. ………………7分
解得x＝1.5.
∴EF为1.5 cm. ………………………………………………………9分
八、（本题10分）
28．（1）证得△ADC≌△CEB；………………………………………2分
证得DE＝AD＋BE；…………………………………………5分
（2）DE=AD－BE；………………………………………………………7分
（3）DE=BE－AD. ………………………………………………………8分
证明. ………………………………………………………………10分