九年级数学期中练习卷（2）
一、选择题(每小题2分，共24分)
1．已知等腰三角形的一个底角等于36°，则这个等腰三角形的顶角等于 （ B ）
A．148° B．108° C．72° D．36°
2．一元二次方程x2 －x = 0的根为 （ C ）
A．x = 0 B．x = 1
C．x 1 = 0，x 2 = 1 D．x 1 = 0，x 2 = －1
3．依次连接各边中点，所得图形是菱形的是 （ ）
A.任意四边形 B.梯形 C.矩形 D.菱形
4、当m＜0时，化简
的结果是
( )
A、-1 B、1 C、m D、-m.
5．平行四边形、矩形、菱形、正方形都具有的性质 （ B ）
A．对角线相等 B．对角线互相平分
C．对角线平分一组对角 D．对角线互相垂直
6．将方程
左边变成完全平方式后，方程是
（ ）
A．
B．
C．
D．
７．如果
在实数范围内有意义，那么x的取值范围是
（ ）
A、x≠2 B、x＜2 C、x＞2 D、x≥2
8、一元二次方程
的根的情况是
（ ）
A．有两个不相等的实数根 B．有两个相等的实数根
C．没有实数根 D．无法判断
9、若关于x的方程
无实根，则k可取的最小整数为 （ ）
A、2 B、1 C、0 D、
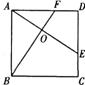
10．如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，
AE、BF相交于点D，下列结论①AE=BF；②AE⊥BF；③ AO=OE；
④S△AOB =S四边形DEOF中，错误的有 ( )
A．4个 B．3个 C．2个 D．1个
二、填空题(每小题3分,共12分)
11． 某同学参加校田径运动会跳远比赛，6次试跳的成绩分别为4.35m，4.22m，4.63m，4.70m，4.41m，4.45m，该同学试跳成绩的极差为 m．
12、若一组数据1、2、3、x的极差是6，则x的值为 ．
13、
是关于x的方程 (x － a)(x
－ 2)＝ 0的一个解， 则a =
．
14．化简
。
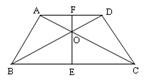15．如图，等腰梯形ABCD中，AD∥BC，对角线AC，BD相交于O，
过O作EF
BC，分别交AD，BC于F，E两点，则图中全等三角
形有______对。
16、已知直角三角形的面积为5
，一条直角边的长为
，则它的
另一条直角边的长为 。
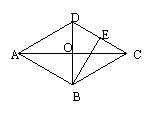
17、已知：菱形ABCD中，对角线AC = 16 cm，BD = 12 cm，
BE⊥DC，垂足为E，则BE的长为 ．
18．一个等腰三角形的一个角为30°，腰长为4cm，那么，该三角形的面积等于 ．
三:解答题 (每小题5分，共20分)
19、
。
20、
。
21．解方程 x2
－ 4
x ＋1 = 0。
22、解方程：
。
四、说理与证明 (第23、24题每小题6分，第25题8分，共20分)
23、某射击队的甲、乙两位运动员在一次比赛中分别射击10次，他们的成绩如下：
| 甲 | 8 | 8 | 9 | 5 | 9 | 10 | 7 | 9 | 6 | 9 |
| 乙 | 7 | 7 | 8 | 7 | 8 | 9 | 8 | 9 | 9 | 8 |
试运用所学知识说明谁的成绩好。
24、如图，在□ABCD中，点E、F分别在CD、AB的延长线上，且AE=AD，CF=CB．
求证：（1）DE = BF；
（2）四边形AFCE是平行四边形。
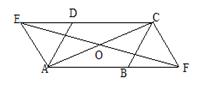
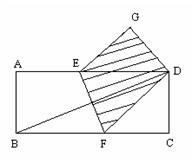25、如图：把矩形纸片ABCD按如图方式折叠，使顶点B和D重合，折痕为EF，连接BD．
求证：（1）△DEF是等腰三角形；
（2）BD⊥EF。
五、（本题满分8分）
26．已知，一个三角形两边长分别是6和8，第三边长是x2－16x＋60=0的一个实数根，试求第三边的长及该三角形的面积.
六、（本题满分8分）
27．据报道，我省农作物秸杆的资源巨大，但合理利用量十分有限，2006年的利用率只有30%，大部分秸杆被直接焚烧了，假定我省每年产出的农作物秸杆总量不变，且合理利用量的增长率相同，要使2008年的利用率提高到60%，求每年的增长率。(取
≈1.41)
七、(本题8分)
28．如图，梯形ABCD中，AD∥BC，AB ＝CD ＝ 3 cm，∠C ＝ 60°，BD⊥CD．
（1）求BC、AD的长；
（2）有一个动点P从点B开始沿BC边向点终C以1 cm/s的速度运动，试写出四边形APCD的面积S 与运动时间t之间的函数关系式；
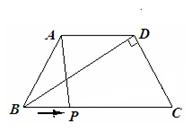（3）当t为何值时，△BPD是等腰三角形？说明你的理由。
参考答案
一、
1．B 2。C 3。C 4。A 5。B 6。A 7。C 8。A 9。D 10。D
二、
11．0．48 12。7或-3 13。1
14。
15。5对 16。
17．
18。4或
三、
19．解：原式=
=
20．解：原式=
=
21．解：
。 
， 
。
22．解：
。
。
四、
23．略
24．证：（1）∵四边形ABCD是平行四边形，∴AD=CB，∠ADC=∠ABC。∴∠ADE=∠CBF。
由AE=AD，CF=CB可得，∠ADE=∠AED，∠CBF=∠CFB。
∴在△ADE和△CBF中，∠ADE=∠CBF ，∠AED =∠CFB， AD=CB，
∴△ADE≌△CBF。∴DE = BF。
（2）∵AB∥CD，AB=CD，DE = BF，
∴AF∥CE，AF=CE。
∴四边形AFCE是平行四边形．
25．证明：（1）由矩形ABCD可得AD∥BC ，∴∠BFE=∠DEF。
有由折叠可得∠BFE=∠DFE。∴∠DFE=∠DEF。∴DE=DF。
即 △DEF是等腰三角形。
（2）连接BE，可证四边形BFDE是菱形。∴BD⊥EF。
五、
26、解：解方程，可得x=6，或x=10。即第三边的长为6或10 。
当第三边的长为6时，三角形的面积=
（平方单位）
当第三边的长为10时，三角形的面积=24（平方单位）
六、（本题8分）
27．解：设我省每年产出的农作物秸杆总量为a，合理利用量的增长率是x，……1分
由题意得： 30%a（1＋x）2=60%a，即（1＋x）2=2…………5分
∴x1≈0.41，x2≈－2.41(不合题意舍去)。……7分
∴x≈0.41。……8分
七．（本题8分）
28．（1）BC ＝2CD ＝ 6 cm，AD ＝AB ＝ 3 cm，
（2）当P点从B点出发运动t秒时，BP ＝2t，∴PC ＝6－ t．
过D作DE⊥BC于E，则DE ＝BD=
t, S梯形APCD＝ ´（AD +
PC）·DE＝
．
（3）∵∠C ＝ 60°，∴∠CBD=30°。
若BP=DP，则BP=
BC=3，此时t=3；
若BD=BP，则BP=
，此时t=。