| 题目 | 一题 | 二题 | 三题 | 四题 | 总分 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
|
|
|
|
九年级数学第二次月考试卷
时间：120分钟 满分：100分
一、选择题（请把正确选项写在答案卷上，每题3分，共计30分）
1、 式子
在实数范围内有意义，则X的取值范围是（ ）
（A）
≥
（B）
（C）≤2
（D）≥2
2、 下列根式中，最简二次根式是（ ）
A. B. C. D.
3、 有一人患了流感，每轮传染中平均一个人传染了个人，则经过两轮传染后，患流感的总人数400，所列方程是 （
）
（A）
=400
（B）
=400
（C）
=400
（D）
=400
4、“从布袋中取出一个红球的概率为0”，这句话的含义是（ ）
(A) 布袋中红球很少 (B) 布袋中全是红球
(C) 布袋中没有红球 (D) 不能确定
5、扇形的半径为30cm，圆心角为120°，此扇形的弧长是（ ）
（A）10 cm （B）20 cm （C）10πcm （D）20πcm
6、下列事件中是必然事件的是（ ）。
（A）太阳每天都从东方升起 ； （B）度量三角形的内角和结果是360°；
（C）投掷一枚硬币，正面向上； （D）某射击运动员射击一次，中靶心。
7、下面四张扑克牌中，属于中心对称图形的是（ ）
 |
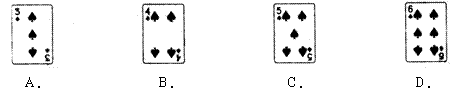8、⊙O的半径R=5cm，点P与圆心O的距离OP=3cm，则点P与⊙O的位置关系是（ ）。
（A）点P在⊙O外 （B）点P在⊙O上
（C）点P在⊙O内 （D）不确定
9、如图所示三圆同心于点O，AB=4cm，CO⊥AB于O，则图中阴影部分的面积为（ ）。
(A) 4cm2 (B)1cm2 (C)4兀cm2 (D)兀cm2
10、 如图，水平放置的一个油管的截面半径为13cm，其中有油部分油面宽
为24cm，则截面上有油部分油面高
（单位：cm）等于（ ）
（A）8cm （B）9cm（C）10cm（D）11cm
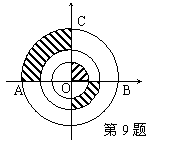
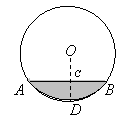
二、填空题（每小题2分，共20分）
1、方程
的解是
.
2、从6名男同学和2名女同学中派一名同学去观看排球比赛，男同学被派去的概率是 .
3、如图，一个油桶靠在墙边，量得WY=2m，并且XY⊥WY，这个油桶的底面半径是__________。
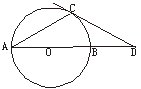
4、如图：A、B、C是⊙O上的三点，∠BAC= 45°，则∠BOC=____
5、如图，在“世界杯”足球比赛中，甲带球向对方球门PQ进攻。当他带球冲到A点时，同伴乙已经助攻冲到B点。有两种射门方式：第一种是甲直接射门；第二种是甲将球传给乙，由乙射门。仅从射门角度考虑，应选择第 种射门方式。
 |
6、已知点A（－3，－2），点B与点A关于原点对称，点C与点A关于X轴对称，则点B、C的坐标分别是B（ ）、C（ ）。
7、半径为3的一个圆与另一个圆相切，而且圆心距为5，则另一个圆的半径是____________.
8、一个直角三角形的两条直角边长是方程
的两个根，则此直角三角形的外接圆的半径是
9、如图：点D是等边△ABC的边BC上一点，△ABD绕点A逆时针旋转到
△ACE的位置 ，则∠DAE＝
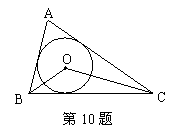
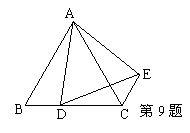10、如图所示，⊙O为△ABC的内切圆，
，
，
则
三、解答下列问题（每小题4分，共20分）
1、计算： 
+（
）2 +（
）0
2、解方程：
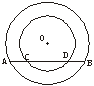
3、如图：两个同心圆，作一直线交大圆于A、B，交小圆于C、D，AC与BD有何关系？请说明理由.
4、已知a、b均为正数。
Ⅰ）观察：①若a＋b=2，则≤1 ②若a＋b=3，则≤
③若a＋b=4，则≤2 ……
Ⅱ）猜想：①若a＋b=2000，则≤___________，
②若a＋b=m，则≤____________
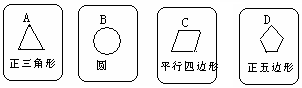
5、有四张背面相同的纸牌A，B，C，D，其正面分别画有四个不同的几何图形（如图）．小华将这4张纸牌背面朝上洗后摸出一张，放回洗后再摸出一张．求：两次摸出的牌面图形都既是中心对称图形又是轴对称图形的纸牌的概率．
 |
四、（每小题6分，共30分）
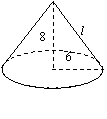
1、如图：圆锥的底面半径为6cm，高为8cm，求（1）这个圆锥的侧面积（4分）；（2）这个圆锥的全面积。（2分）
2、如图AB在⊙O的直径，点D在AB的延长线上,且BD=OB,点C在⊙O上,
∠CAB=30°。
(1)CD是⊙O的切线吗？说明你的理由;（4分）
(2)AC=_____，请给出合理的解释. （2分）
3、甲、乙、丙三位小朋友做写1、2、3数字游戏，每人随机写出一个数字。解决下列问题：
（1）用适当的方法表示所有可能出现的结果有多少种？（2分）
（2）求三个人写出相同数字的概率；（2分）
（3）求其中至少有两个人写的是数字“1”的概率是多少？（2分）
4、某商店进购某种商品出售，若按每件盈利2元售出，每天可售出200件，现在采取提高商品售价减少销售量的办法增加利润，如果这种商品每件的销售价每提高1元，其销售量就减少10件，问应将每件商品提高多少元出售时，才能使平均每天利润为1210元？（6分）
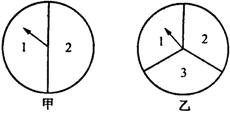5、小华和小红用如图所示的两个转盘做游戏，游戏规则如下：分别顺时针旋转两个转盘，当两个转盘所转到的数字之积为奇数时，小华得2分；当所转到的数字之积为偶数时，小红得2分。问：
（1）这个游戏对双方公平还是不公平？说明理由。（4分）
（2）若不公平，如何修改游戏规则才能使游戏对双方公平？（2分）
九年级数学第二次月考参考答案
一、 DCACD； ABCDA。
二、 （1）X=±5；（2）3／4 ；（3）2m；（4）90°；（5）第二种；（6）
B（3，2）、C（－3，2）；（7）2或8；（8）2.5；（9）60°；（10）120°
三、1、7； 2、X1=7，X2=－2； 3、AC=BD，理由略。 4、1000，m/2；
5、图或表略，共有16种可能的结果，其中既是中心对称图形又是轴对称图形的只有一种：（BB），每种出现的可能性相等；∴P（都既是中心对称图形又是轴对称图形）=1/16。
四、1、（1）S侧=60πcm2 （2）S全=96πcm2
2、（1）CD是⊙O的切线。理由提示：连接OC、BC，证OC⊥CD。
（2）AC=CD，理由：由（1）得∠CAB=30°∠D=30°∴∠CAB=∠D
∴AC=CD。
3、（1）树形图略，共有27种可能出现的结果；
（2）P（三人写出数字都相同）=3/27=1/9；
（3）P（至少两人是写1）=7/27。
4、解：设每件商品应提高X元出售时，才能使平均每天利润为1210元，得
（2+X）（200—10X）=1210
即—10X2+180X—810=0
即 X2-18X+81=0
∴（X-9）2=0
∴X1=X2=9
答：略。
5、解：列表或画树形图：
| 乙 甲 | 1 | 2 | 3 | |
| 1 | 1×1=1 | 2×1=2 | 3×1=3 | |
| 2 | 1×2=2 | 2×2=4 | 3×2=6 | |
|
| |||
（1）由表或图可知：共有6种可能的结果出现，它们出现的可能性相等；其中
积=奇数（2种）；积=偶数（4种）
∴P（积为奇数）=2/6=1/3；
∴P（积为偶数）=4/6=2/3；
∴小华得分：1/3×2=2/3
∴小红得分：2/3×2=4/3
∴这个游戏对双方不公平。
（2）（方法多种，能使双方得分相等即可）其一：将数字之积为奇数时小华得2分改为得4分，则对双方公平。