九年级数学(下)第一次月考试卷
数 学 试 题
一、选择题(本大题共12个小题,每小题3分,共36分)。
1.下列计算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.下列函数中,自变量x的取值范围是x>2的函数是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3. 关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0,则a的值为( )
A. 1 B. -1 C. 1或-1 D. 0
4.如图,将正方形图案绕中心O旋转180°后,得到的图案是 ( )

5.某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成,其俯视图如图所示,则此工件的左视图是( )
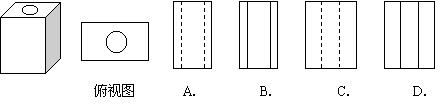 |
6.如图,![]() 内接于⊙O,
内接于⊙O,![]() ,
,![]() ,则⊙O的半径为( )
,则⊙O的半径为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

 | |||
 | |||
7.正方形网格中,![]() 如图放置,则
如图放置,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边![]() 为直径的半圆内种菜,他家养的一只羊平时拴在
为直径的半圆内种菜,他家养的一只羊平时拴在![]() 处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
A.3m B.5m C.7m D.9m
9.随机掷一枚均匀的硬币两次,落地后至少有一次正面朝上的概率是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 10.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运
10.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运
动,连结DP,过点A作AE⊥DP,垂足为E,设DP=![]() ,AE=
,AE=![]() ,
,
则能反映![]() 与
与![]() 之间函数关系的大致图象是( )
之间函数关系的大致图象是( )




A B C D
11.已知:二次函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.当![]() 时,
时,![]() 随
随![]() 的增大而减小 B.若图象与
的增大而减小 B.若图象与![]() 轴有交点,则a≤4
轴有交点,则a≤4
C.当![]() 时,不等式
时,不等式![]() 的解集是
的解集是![]()
D.若将图象向上平移1个单位,再向左平移3个单位后过点![]() ,则
,则![]()
12.如图,正方形![]() 的面积为1,
的面积为1,![]() 是
是![]() 的中点,则图中阴影部分的面积是( )
的中点,则图中阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
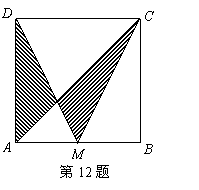 | |||
 | |||
二.填空题(本大题共4个小题,每小题4分,共16分)
13.已知:关于![]() 的一元二次方程
的一元二次方程![]() 没有实数根,其中
没有实数根,其中![]() 、
、![]() 分别为
分别为
⊙O1和⊙O2的半径,![]() 为此两圆的圆心距,则⊙O1和⊙O2的位置关系为
。
为此两圆的圆心距,则⊙O1和⊙O2的位置关系为
。
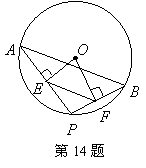
14.如图,点![]() 是上⊙O两点,
是上⊙O两点,![]() ,点
,点![]() 是⊙O上的动点(
是⊙O上的动点(![]() 与
与![]() 不重合),连结
不重合),连结![]() ,过点
,过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() ,则
,则![]() .
.
15.如图,已知![]() ,点
,点![]() 在
在![]() 边上,四边形
边上,四边形![]() 是矩形.请你只用无刻度的直尺在图中画出
是矩形.请你只用无刻度的直尺在图中画出![]() 的平分线(请保留画图痕迹).
的平分线(请保留画图痕迹).
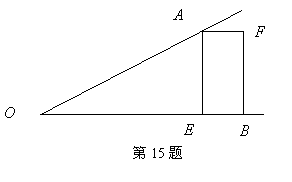
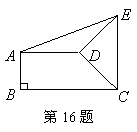
16.如图,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,将腰
,将腰![]() 以点
以点![]() 为中心逆时针旋转
为中心逆时针旋转![]() 至
至![]() ,连结
,连结![]() ,则
,则![]() 的面积是 .
的面积是 .
三.解答题(本大题共8个小题,共68分)
17.(本小题满分6分)计算:![]()
18.(本小题满分6分)解方程:x2+3=3(x+1)
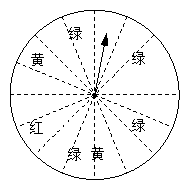
19.(本小题满分7分)在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券10元.
(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费125元,你会选择转转盘还是直接获得购物券?说明理由.
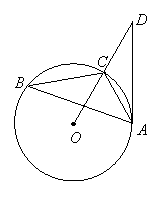
20.(本小题满分8分)如图,已知:![]() 内接于
内接于![]() ,点D在OC的延长线上,
,点D在OC的延长线上,![]() ,
,![]() . (1)求证:
. (1)求证:![]() 是⊙O的切线; (2)若
是⊙O的切线; (2)若![]() ,求
,求![]() 的长.
的长.
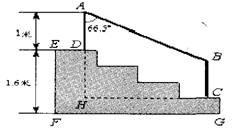
21.(本小题满分9分)某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为l.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66. 5°.
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度![]() (即AD+AB+BC,结果精确到0.1米).
(即AD+AB+BC,结果精确到0.1米).
(参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
22.(本小题满分10分)某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
| 型号 | A | B |
| 成本(万元/台) | 200 | 240 |
| 售价(万元/台) | 250 | 300 |
⑴该厂对这两型挖掘机有哪几种生产方案?
⑵该厂如何生产能获得最大利润?
⑶根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产获得最大利润?(注:利润=售价-成本)
23.(本小题满分10分)请阅读下列材料:
问题:如图(2),一圆柱的底面半径为5dm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线。小明设计了两条路线:
路线1:侧面展开图中的AC。如下图(2)所示:
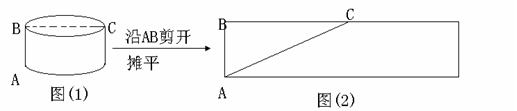
设路线1的长度为![]() ,则
,则![]()
路线2:高线AB + 底面直径BC。如上图(1)所示:
设路线2的长度为![]() ,则
,则![]()
![]()
∴![]() ∴
∴![]() 所以要选择路线2较短。
所以要选择路线2较短。
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1dm,高AB为5dm”继续按前面的路线进行计算。请你帮小明完成下面的计算:
路线1:![]() ___________________;
___________________;
路线2:![]() __________
__________
∵![]() ∴
∴ ![]() (填>或<) 所以应选择路线_________(填1或2)较短.
(填>或<) 所以应选择路线_________(填1或2)较短.
|
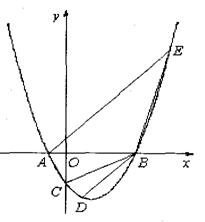
24.(本小题满分12分)设抛物线![]() 与x轴交于两个不同的点A(一1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
与x轴交于两个不同的点A(一1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线![]() 交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.