08年北京市中考模拟分类汇编⑽
几何综合
1.
(大兴一模)矩形ABCD中,AD=2,![]() ,现将一个直径MN为2的量角器如图25-1摆放,使其
,现将一个直径MN为2的量角器如图25-1摆放,使其![]() 线的端点N与C重合,M与B重合,O为MN的中点,量角器的半圆弧与矩形ABCD的对角线AC、BD分别交于P、Q,设P、Q在量角器上的读数分别是
线的端点N与C重合,M与B重合,O为MN的中点,量角器的半圆弧与矩形ABCD的对角线AC、BD分别交于P、Q,设P、Q在量角器上的读数分别是![]() 、
、![]() .
.
⑴ 求![]() 与
与![]() 之间的函数关系式.(不必写出自变量的取值范围).
之间的函数关系式.(不必写出自变量的取值范围).
⑵ 将量角器绕C点逆时针旋转,使它的直径落在AC上,如图25-2所示,![]() 为
为![]() 的中点,此时量角器的半圆弧交DC于K,若K点的读数为
的中点,此时量角器的半圆弧交DC于K,若K点的读数为![]() ,那么
,那么![]() 与
与![]() 的数量关系是什么,请说明理由.
的数量关系是什么,请说明理由.
⑶ 如图25-2所示,若![]() ‖
‖![]() ,求出此时AB的长.
,求出此时AB的长.
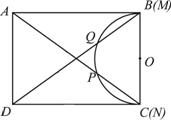
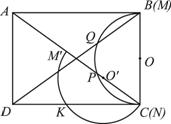

图25-1 图25-2 图25-3
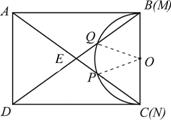
【答案】⑴ 连结OQ、OP
∵ABCD是矩形,
∴AC=BD.
∴BE=CE.
∴∠EBO=∠OCE
∵OQ=OB, 图25-1
∴∠EBO=∠OQB.
∴∠BOQ=180°-2∠EBO.
同理可证
∠COP=180°-2∠OCE.
∴∠BOQ=∠COP= x°. ……………………2分
∴y°=∠COQ=180°-∠BOQ=180°-x°
∴y =180-x. ………………………3分
⑵ z与y的数量关系是:z=y ……………………4分
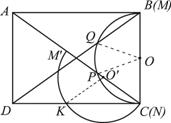 如图25-2,连结O′K、OP、OQ.
如图25-2,连结O′K、OP、OQ.
∵∠ACD+∠BCA=90°,
∴∠ACD=90°-∠BCA.
∴z°=180°-2∠ACD
=180°-2(90°-∠BCA )
=2∠BCA
=180°-∠COP. 图25-2
∴z =180-x.
∵y=180-x,
∴z=y. ……………………………5分
⑶ 如图25-3,连结B M′、M′K、KO
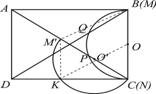 ∵M′C是量角器的直径,
∵M′C是量角器的直径,
∴∠M′KC=90°.
∵∠BCD=90°,
∴∠M′KC+∠BCD=180°. 图25-3
∴BO∥M′K.
∵M′B∥KO,
∴M′KOB是平行四边形,………………………………6分
∴M′K=BO=![]() BC=1.
BC=1.
∵M′C=MN=2,
∴M′K=![]() M′C.
M′C.
∴∠ACD=30°. ……………………………………7分
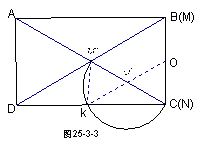 ∴AC=4
∴AC=4
∴![]()
∴M′与对角线的交点重合如图25-3-3,
在Rt△ADC中,
∵AD=2,
∴DC=2![]() .
.
∵ABCD是矩形,
∴DC=AB=2![]() . ……………………………8分
. ……………………………8分
2.
(丰台一模)如图,![]() 为直角三角形,
为直角三角形,![]() ,
,![]() ,
,![]() ;四边形
;四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,且点
,且点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,点
在同一条直线上,点![]() 与点
与点![]() 重合.
重合.
⑴ 求边![]() 的长;
的长;
⑵ 将![]() 以每秒
以每秒![]() 的速度沿矩形
的速度沿矩形![]() 的边
的边![]() 向右平移,当点
向右平移,当点![]() 与点
与点![]() 重合时停止移动,设
重合时停止移动,设![]() 与矩形
与矩形![]() 重叠部分的面积为
重叠部分的面积为![]() ,请求出重叠部分的面积
,请求出重叠部分的面积![]() (
(![]() )与移动时间
)与移动时间![]() 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);
⑶ 在⑵的基础上,当![]() 移动至重叠部分的面积为
移动至重叠部分的面积为![]()
![]() 时,将
时,将![]() 沿边
沿边![]() 向上翻折,得到
向上翻折,得到![]() ,请求出
,请求出![]() 与矩形
与矩形![]() 重叠部分的周长(可利用备用图).
重叠部分的周长(可利用备用图).
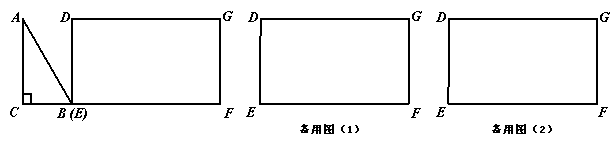
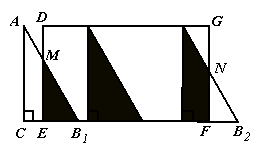 【答案】⑴ ∵
【答案】⑴ ∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() .………
.………![]() 分
分
⑵ ①当![]() 时,
时,![]()
∴![]() ,
,
∴![]() . ……………………………
. ……………………………![]() 分
分
② 当![]() 时,
时,![]() .……………………………
.……………………………![]() 分
分
③ 当![]() 时,
时,![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,∴
,∴![]() .…………………………
.…………………………![]() 分
分
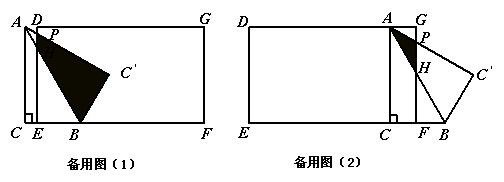
⑶ ①当![]() ,且
,且![]() 时,
时,
即![]() ,解得
,解得![]() (不合题意,舍去).
(不合题意,舍去).
∴![]() .
.
由翻折的性质,得![]() ,
,![]() ,
,![]() .
.
∵![]() ∥
∥![]() ,∴
,∴![]()
∵![]() ,
,
∴![]()
∴重叠部分的周长=![]() ……
……![]() 分
分
②解法与①类似,当![]() ,且
,且![]() 时,
时,
即![]() ,解得
,解得![]() (不合题意,舍去).
(不合题意,舍去).
重叠部分的周长=![]() .
.
∴当![]() 时,重叠部分的周长为
时,重叠部分的周长为![]() .……
.……![]() 分
分
3.  (宣武一模)如图,正方形
(宣武一模)如图,正方形![]() 边长为6,菱形
边长为6,菱形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 分别在正方形
分别在正方形![]() 的边
的边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,联结
,联结![]() 。
。
⑴ 当![]() 时,试求菱形
时,试求菱形![]() 的边长与
的边长与![]() 的面积;
的面积;
⑵ 设![]() ,试用含
,试用含![]() 的代数式表示
的代数式表示![]() 的面积;
的面积;
⑶ 请判断![]() 的面积能否等于1,并说明理由.
的面积能否等于1,并说明理由.

【答案】⑴ 如图1,菱形![]() 边长为
边长为![]() ,可证菱形
,可证菱形![]() 是
是
正方形,进一步可得出![]() ≌
≌![]() .
.
因此![]() ,
,
即点![]() 在
在![]() 边上,同样可得
边上,同样可得![]() .
.
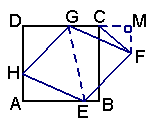 因此
因此![]() .………………………………… 3分 (第23题图1)
.………………………………… 3分 (第23题图1)
⑵ 如图2,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
联结![]() .可证
.可证![]() ≌
≌![]() ,
,
所以![]() ,
,
即无论菱形![]() 如何变化,
如何变化,
点![]() 到直线
到直线![]() 的距离始终为定值2,
的距离始终为定值2,
因此![]() . ……………………… 6分 (第23题图2)
. ……………………… 6分 (第23题图2)
⑶ 若![]() ,由⑵可知
,由⑵可知![]() ,得
,得![]() .此时,
.此时,
在![]() 中,
中,![]() .相反地,在
.相反地,在![]() 中,
中,
![]() >
>![]() ,与题意不合.故不可能
,与题意不合.故不可能![]() .…………………………… 7分
.…………………………… 7分
4.
(宣武一模)在坐标平面上,点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以
方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以![]() 为对角线的矩形
为对角线的矩形![]() 的边长
的边长![]() ;过点
;过点![]() 且垂直于射线
且垂直于射线![]() 的直线
的直线![]() 与点
与点![]() 同时出发,且与点
同时出发,且与点![]() 沿相同的方向、以相同的速度运动.
沿相同的方向、以相同的速度运动.
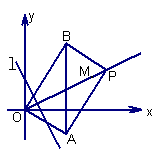 ⑴ 在点
⑴ 在点![]() 运动过程中,试判断
运动过程中,试判断![]() 与
与![]() 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
⑵
设点![]() 与直线
与直线![]() 都运动了
都运动了![]() 秒,求此时的矩形
秒,求此时的矩形![]() 与直线
与直线![]() 在运动过程中所扫过区域的重叠部分的面积
在运动过程中所扫过区域的重叠部分的面积![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
【答案】⑴ ![]() 轴.……………… 1分
轴.……………… 1分
理由:如图1![]()
![]() 中,
中,![]()
![]() ,
,
![]() .
.
设![]() 交
交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
![]() 矩形的对角线互相平分且相等,则
矩形的对角线互相平分且相等,则![]() ,
,
![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 轴.……………… 3分
轴.……………… 3分
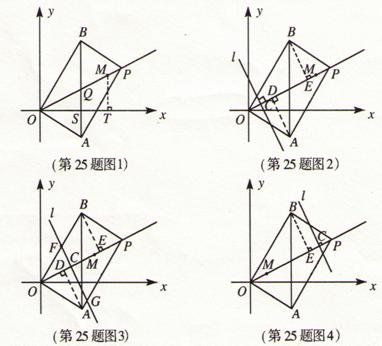
⑵ 设![]() 在运动过程中与射线
在运动过程中与射线![]() 交于点
交于点![]() ,过点
,过点![]() 且垂直于射线
且垂直于射线![]() 的直线交
的直线交![]() 于点
于点![]() ,过点
,过点![]() 且垂直于射线
且垂直于射线![]() 的直线交
的直线交![]() 于点
于点![]() ,则
,则![]() .
.
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .………… 4分
.………… 4分
①当![]() ,即
,即![]() 时,(如图2)
时,(如图2)![]() . …………………5分
. …………………5分
②当![]() ,即
,即![]() 时,(如图3)设直线
时,(如图3)设直线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
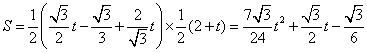 .…………………………6分
.…………………………6分
③当![]() ,即
,即![]() 时,(如图4)
时,(如图4)![]() ,
,
![]()
![]() . ………………………………………………7分
. ………………………………………………7分
5.
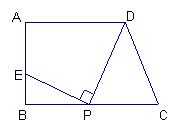 (昌平二模)如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=
(昌平二模)如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=![]() ,在线段BC上取一点P,连结DP,作射线PE⊥DP,PE与直线AB交于点E.
,在线段BC上取一点P,连结DP,作射线PE⊥DP,PE与直线AB交于点E.
⑴ 试确定CP=3时,点E的位置;
⑵ 若设CP=x,BE=y,试写出y关于自变量x的函数关系式;
⑶ 若在线段BC上找到一点P,使上述作法得到的点E与点A重合,试求出此时![]() 的值.
的值.
【答案】⑴ 当CP=3时
∵BC=12,AD=9
∴BP=9
∴AD=BP
∵AD∥BC,∠ABC=90°
∴四边形ABPD是矩形
∴∠DPB=90°
又 ∵PE⊥DP
∴∠DPE=∠DPB =90°且点E在AB上
∴点E与点B重合……………………2分
⑵ 作DM⊥BC于M
当点P在BM上时
∴∠DMB=∠DMC=∠ABC =90°
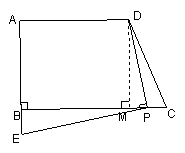 ∴∠1+∠3=90°
∴∠1+∠3=90°
∵PE⊥DP
∴∠DPE=90°
∴∠1+∠2=90°
∴∠3=∠2
又∵∠ABC =∠DMB
∴![]() ∽
∽![]()
∴![]()
同(1)可证四边形ABDM是矩形
∴AB=DM=![]()
∵设CP=x,BE=y
∴MP=![]() -3,BP=12-
-3,BP=12-![]()
∴![]()
∴![]() ……………………5分
……………………5分
当点P在MC上时,如图,同理可得
![]() ……………………6分
……………………6分
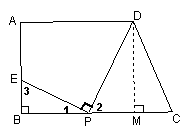 ⑶ 若在线段BC上找到一点P,使上述作法得到的点E与点A重合,则BE=AB=
⑶ 若在线段BC上找到一点P,使上述作法得到的点E与点A重合,则BE=AB=![]() ,且点P在BM上
,且点P在BM上
∴![]()
∴![]() ……………………7分
……………………7分
由题意:![]()
即![]() ……………………8分
……………………8分
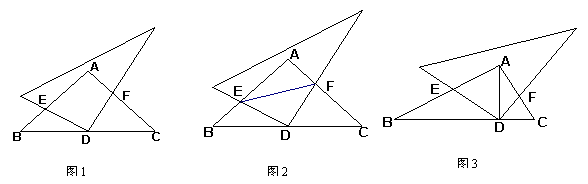
6. (昌平二模)△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,把一个三角板的直角顶点放在点D处,将三角板绕点D旋转且使两条直角边分别交AB、AC于E、F .
⑴ 如图1,观察旋转过程,猜想线段AF与BE的数量关系;
⑵ 如图2,若连接EF,请探索线段BE、EF、FC之间的联系;
⑶ 如图3,若将“AB=AC,点D是BC的中点”改为:∠B=30°,AD⊥BC于点D,其余条件不变,探索(1)中结论是否成立?若不成立,请探索关于AF、BE的比值.
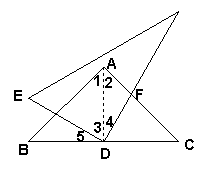
【答案】⑴ 连接AD
∵AB=AC,∠BAC=90°,点D是BC的中点
∴AD=BD=DC=![]() BC , ∠ADB=∠ADC=90°
BC , ∠ADB=∠ADC=90°
∴∠B=∠C=∠1=∠2=45°
∴∠3+∠5==90°
∵∠3+∠4==90°
∴∠5=∠4
 ∵ BD=AD
∵ BD=AD
∴∠B=∠2
∴![]()
∴BE=AF……………………3分
⑵ 由(1)BE=AF
又∵AB=AC
∴AE=CF
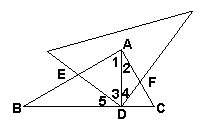 在
在![]() 中,
中,![]()
∴![]() ……………………6分
……………………6分
⑶ ⑴中的结论BE=AF不成立
∵∠B=30°,AD⊥BC于点D
∴∠3+∠5==90°, ∠B+∠1==90°
∵∠3+∠4==90°,∠1+∠2==90°
∴∠B=∠2 , ∠5=∠4
∴![]() ∽
∽![]()
∴![]() ……………………9分
……………………9分