08年北京市中考模拟分类汇编⑷
函数
一、函数基本知识
1.
(海淀一模)函数![]() 中,自变量
中,自变量![]() 的取值范围是 .
的取值范围是 .
【答案】
![]()
2.
(朝阳一模)函数![]() 中,自变量
中,自变量![]() 的取值范围是( )
的取值范围是( )
![]() 且
且![]()
![]()
![]() 且
且![]()
![]()
【答案】
![]()
3.
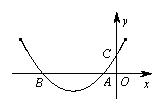 (朝阳一模)如图,抛物线
(朝阳一模)如图,抛物线![]() ,
,![]() ,下列关系中正确的是( )
,下列关系中正确的是( )
![]()
![]()
![]()
![]()
【答案】 A
4.
(大兴一模)函数![]() 自变量
自变量 ![]() 的取值范围是( )
的取值范围是( )
![]()
![]()
![]()
![]()
【答案】 B
5.
(大兴一模)若反比例函数![]() 的图象上有两点
的图象上有两点![]() ,
,![]() ,则
,则![]() _____
_____![]() (填“
(填“![]() ”或“
”或“![]() ”或“
”或“![]() ”).
”).
【答案】
![]() .
.
6. (丰台一模)写出一个图像在第二、第四象限的反比例函数的解析式 .
【答案】![]() (答案不惟一)
(答案不惟一)
|
| -1 | 0 | 1 |
|
| 1 |
| -1 |
7.
(宣武一模)已知一次函数![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ),
),![]() 与
与![]() 的部分对应值如表所示,那么
的部分对应值如表所示,那么![]() 的值等于( ).
的值等于( ).
(A)![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
【答案】
![]()
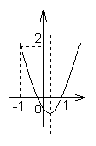
8.
(宣武一模)如图,二次函数![]() 的图象开口向上,图象经过点
的图象开口向上,图象经过点![]() 和
和![]() ,且与
,且与![]() 轴相交于负半轴,给出四个结论:①
轴相交于负半轴,给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的序号是 .
.其中正确的序号是 .
【答案】 ①④
9. (石景山二模)如图所示:边长分别为1和2的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形.设穿过的时间为t,大正方形内除去小正方形部分的面积为S(阴影部分),那么S与t的大致图象应为 ( )
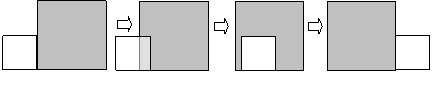
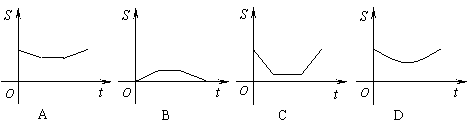
![]()
【答案】 A.
10.
(昌平二模)如果反比例函数![]() 的图象经过点
的图象经过点![]() ,那么
,那么![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】 A
二、函数综合
1.
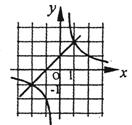 (大兴一模)如图2,是一次函数
(大兴一模)如图2,是一次函数![]() 与反比例函数
与反比例函数![]() 的图象,则关于
的图象,则关于![]() 的方程
的方程![]() 的解为( )
的解为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】
![]()
2.
(海淀一模)已知一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,直线
,直线![]() 经过
经过![]() 上的三分之一点
上的三分之一点![]() ,且交
,且交![]() 轴的负半轴于点
轴的负半轴于点![]() ,如果
,如果![]() ,求直线
,求直线![]() 的解析式.
的解析式.
【答案】
∵直线![]() 与
与![]() 轴,
轴,![]() 轴交点为
轴交点为![]() ,
,
∴两点坐标分别为![]() ,
,
∴![]() ,
,
∴![]()
∵![]() 为
为![]() 上的三分之一点,
上的三分之一点,
∴![]() 点的坐标为
点的坐标为![]() 或
或![]() ,
,
∵![]()
∴当![]() 是,
是,![]() ;当
;当![]() 时,
时,![]() ,
,
∵点![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,
∴![]() 点的坐标为
点的坐标为![]() 或
或![]()
∴直线![]() 的解析式为
的解析式为![]() 或
或![]()
3.
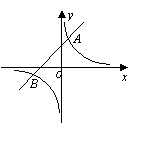 (宣武一模)如图,反比例函数
(宣武一模)如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() (1,3)、
(1,3)、![]() (
(![]() ,
,![]() )两点.
)两点.
⑴ 求反比例函数与一次函数的解析式;
⑵ 根据图象回答:当![]() 取何值时,反比例函数的值大于一次函数的值?
取何值时,反比例函数的值大于一次函数的值?
【答案】⑴ ![]() 点
点![]() (1,3)在反比例函数
(1,3)在反比例函数![]() 图象上,
图象上,
![]()
![]() ,即
,即![]() .
.
![]() 反比例函数解析式为
反比例函数解析式为![]() . …………………………………………………
1分
. …………………………………………………
1分
又![]() 点
点![]() (
(![]() ,
,![]() )在反比例函数
)在反比例函数![]() 图象上,
图象上,
![]()
![]() ,即
,即![]() .
.
![]()
![]() (
(![]() ,
,![]() ). ………………………………………………………………………… 2分
). ………………………………………………………………………… 2分
又![]() 点
点![]() (1,3)和
(1,3)和![]() (
(![]() ,
,![]() )在一次函数
)在一次函数![]() 图象上,
图象上,
![]()
![]() ,解得
,解得![]()
![]() 一次函数解析式为
一次函数解析式为![]() .…………………………………………………… 3分
.…………………………………………………… 3分
⑵ 由交点![]() (1,3)和
(1,3)和![]() (
(![]() ,
,![]() )可知:
)可知:
当![]() 或
或![]() 时,反比例函数的值大于一次函数的值. ……………………… 5分
时,反比例函数的值大于一次函数的值. ……………………… 5分
4.
(朝阳一模)已知![]() 、
、![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根,其中
的两个实数根,其中![]() 为非负整数,点
为非负整数,点![]() ,
,![]() 是一次函数
是一次函数![]() 与反比例函数
与反比例函数![]() 图象的交点,且
图象的交点,且![]() 、
、![]() 为常数.
为常数.
⑴ 求![]() 的值;
的值;
⑵ 求一次函数与反比例函数的解析式.
【答案】
⑴ 依题意,得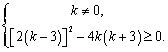 ……………………………………1分
……………………………………1分
解得 ![]() 且
且![]() .
.
∵![]() 为非负整数,∴
为非负整数,∴![]() . …………………………………………………2分
. …………………………………………………2分
⑵ 当![]() 时,原方程化为
时,原方程化为![]() .
.
解得![]() .∴
.∴![]() ,
,![]() .
……………………………………………3分
.
……………………………………………3分
把![]() ,
,![]() 和
和![]() 代入
代入![]() ,得
,得![]() .
.
∴一次函数的解析式是![]() .…………………………………………4分
.…………………………………………4分
把![]() ,
,![]() 代入
代入![]() ,得
,得![]() .
.
∴反比例函数的解析式是![]() .………………………………………5分
.………………………………………5分
5.
(丰台一模)一次函数![]() 的图象经过点
的图象经过点![]() ,且分别与
,且分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() .
.
点![]()
![]() 在
在![]() 轴正半轴上运动,点
轴正半轴上运动,点![]()
![]() 在
在![]() 轴正半轴上运动,且
轴正半轴上运动,且![]() .
.
⑴ 求![]() 的值,并在给出的平面直角坐标系中画出该一次函数的图象;
的值,并在给出的平面直角坐标系中画出该一次函数的图象;
⑵ 求![]() 与
与![]() 满足的等量关系式.
满足的等量关系式.
【答案】⑴ 一次函数![]() 的图象经过点 (1,4),
的图象经过点 (1,4),
则 ![]() ,
,![]() ,…………………………………………
,…………………………………………![]() 分
分
∴ ![]() .
.
该函数的图象见右图: …………………………………………![]() 分
分
 ⑵ 函数
⑵ 函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴的交点分别为
轴的交点分别为
![]() 、
、![]() , ………………………
, ………………………![]() 分
分
∵![]() ,设交点为
,设交点为![]() ,
,
则 ![]() ,
,
![]()
∴△![]() △
△![]() ,……………………
,……………………![]() 分
分
∴![]() ,即
,即 ![]()
∴![]() . ………………………………
. ………………………………![]() 分
分
6.
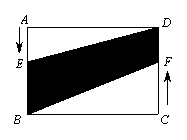 (朝阳一模)如图,在矩形
(朝阳一模)如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 处有一动点
处有一动点![]() 以
以![]() 的速度由
的速度由![]() 向
向![]() 运动,同时点
运动,同时点![]() 处也有一动点
处也有一动点![]() 以
以![]() 的速度由
的速度由![]() 向
向![]() 运动,设运动的时间为
运动,设运动的时间为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围.
的取值范围.
【答案】
依题意,得![]() ,
,![]() .
…………1分
.
…………1分
在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() . …………………………………………………2分
. …………………………………………………2分
∴四边形![]() 的面积=
的面积=![]()
即![]() .…………………………………………………………………4分
.…………………………………………………………………4分
自变量![]() 的取值范围是
的取值范围是![]() .
……………………………………………5分
.
……………………………………………5分
7.
(朝阳一模)已知抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的平行线与抛物线交于点
轴的平行线与抛物线交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,直线
,直线![]() 经过
经过![]() 、
、![]() 两点.
两点.
⑴ 求此抛物线的解析式;
⑵ 连接![]() 、
、![]() 、
、![]() ,试比较
,试比较![]() 和
和![]() 的大小,并说明你的理由.
的大小,并说明你的理由.
【答案】
⑴ ∵![]() 轴且点
轴且点![]() ,
,![]() ,
,
∴设点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
∵直线![]() 经过
经过![]() 点,
点,
∴![]() .∴
.∴![]() .
.
即点![]() ,
,![]() .
.
根据抛物线的对称性,设顶点的坐标为![]() ,
,![]() ,
,
又∵直线![]() 经过
经过![]() 点,
点,
∴![]() ,
,![]() .即
.即![]() ,
,![]() .
.
∴设抛物线的解析式为![]() .
.
∵点![]() ,
,![]() 在抛物线上,∴
在抛物线上,∴![]() .
.
即抛物线的解析式为![]() .……………………………………3分
.……………………………………3分
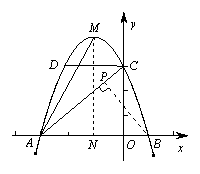 ⑵ 作
⑵ 作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
由⑴中抛物线![]() 可得
可得
点![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() .∴
.∴![]() .
.
![]() .
.
∴![]() .
.
即![]() .…………………………………………………………8分
.…………………………………………………………8分
8.
(昌平二模)抛物线![]() 交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为直线x = -1,B(1,0),C(0,-3).
交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为直线x = -1,B(1,0),C(0,-3).
⑴ 求二次函数![]() 的解析式;
的解析式;
⑵ 在抛物线对称轴上是否存在一点P,使点P到A、C两点距离之差最大?若存在,求出点P坐标;若不存在,请说明理由.
 【答案】⑴ 二次函数的解析式是:
【答案】⑴ 二次函数的解析式是:![]() ……2分
……2分
⑵ ∵ A、B两点关于对称轴![]() 对称
对称
∴ 点A(-3,0)
作直线AC交对称轴于点P ,点P即为所求
设直线AC的解析式是:![]()
∴![]()
∴ ![]()
∴设直线AC的解析式是:![]()
当![]() 时,
时,![]()
∴点P的坐标是(-1,-2)……………………6分
9.
(大兴一模)已知二次函数![]() 的图象和x轴有且只有一个交点A,与y轴的交点为B(0,4),且
的图象和x轴有且只有一个交点A,与y轴的交点为B(0,4),且![]() .
.
⑴ 求该二次函数的解析表达式;
⑵ 将一次函数y=![]() x的图象作适当平移,使它经过点A,记所得的图象为L,图象L与抛物线的另一个交点为C,求△ABC的面积.
x的图象作适当平移,使它经过点A,记所得的图象为L,图象L与抛物线的另一个交点为C,求△ABC的面积.
【答案】⑴ 由B(0,4)得,c=4.
抛物线![]() 与x轴的交点A(
与x轴的交点A(![]() ,0),
,0),
∵![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,即A(-2,0).……1分
,即A(-2,0).……1分
∴![]() 解得
解得![]()
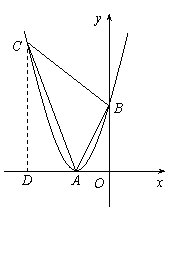 所求二次函数的解析式为
所求二次函数的解析式为![]() .……………………………………………3分
.……………………………………………3分
⑵
设图象L的函数解析式为y=![]() x+b,因图象L过点A(
x+b,因图象L过点A(![]() ,0),
,0),
所以![]() ,即平移后所得一次函数的解析式为
,即平移后所得一次函数的解析式为
y=![]() .………………………………………4分
.………………………………………4分
令![]() =
=![]() ,
,
解得![]() ,
,![]() .
.
将它们分别代入y=![]() ,
,
得![]() ,
,![]() .
.
所以图象L与抛物线![]() 的
的
另一个交点为C(![]() ,9).…………………………………………6分
,9).…………………………………………6分
如图,过C作CD⊥x轴于D,则
S△ABC=S梯形BCDO-S△ACD -S△ABO
=![]() …………………………………………7分
…………………………………………7分
10.
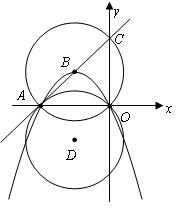 (宣武一模)已知:直线
(宣武一模)已知:直线![]() 交
交![]() 轴、
轴、![]() 轴于
轴于![]() 两点,经过
两点,经过![]() 两点的抛物线
两点的抛物线![]() 的顶点
的顶点![]() 在直线AC上.
在直线AC上.
⑴ 求![]() 两点坐标;
两点坐标;
⑵ 求出该抛物线的函数关系式;
⑶
以![]() 点为圆心,以
点为圆心,以![]() 为半径作
为半径作![]() ,将
,将![]() 沿
沿![]() 轴翻折得到
轴翻折得到![]() ,试判断直线
,试判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
⑷
若![]() 为
为![]() 优弧
优弧![]() 上一动点,联结
上一动点,联结![]() ,问在抛物线上是否存在一点
,问在抛物线上是否存在一点![]() ,使
,使![]() ,若存在,试求出点
,若存在,试求出点![]() 的坐标;若不存在,试说明理由.
的坐标;若不存在,试说明理由.
【答案】⑴ 当![]() 时,
时,![]() ,
,![]() 点坐标为
点坐标为![]()
当![]() 时,
时,![]() ,
,![]() ,
, ![]() 点坐标为
点坐标为![]() ………………………… 1分
………………………… 1分
⑵ ![]() 抛物线
抛物线![]() 经过
经过![]() ,
,![]() ,
,
![]() 对称轴
对称轴![]() , ∴
, ∴![]() .①
.①
当![]() 时,代入
时,代入![]() 得
得![]() ,∴
,∴![]() 点坐标为
点坐标为![]() .
.
![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,
![]()
![]() .②
.②
联立①、②解得![]() .
.
![]() 该抛物线的函数关系式为
该抛物线的函数关系式为![]() .……………………………………………3分
.……………………………………………3分
⑶ ![]() 与
与![]() 相切,理由如下:
相切,理由如下:
联结![]() ,
, ![]() ,
, ![]() .
.
![]()
![]()
![]() .
.
![]() .
.
又![]()
![]() 与
与![]() 相切。 ……………………4分
相切。 ……………………4分
⑷ 存在这样的点![]() ,使得
,使得![]() .
.
设![]() 点坐标为
点坐标为![]() .
.
![]() ,
,
而![]() ,
, ![]() …………………………………5分
…………………………………5分
当点![]() 在
在![]() 轴上方时,
轴上方时,![]() , ∴
, ∴![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() . 解得:
. 解得:![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
![]() .………………………………………………………………6分
.………………………………………………………………6分
当点![]() 在
在![]() 轴下方时,
轴下方时,![]() , ∴
, ∴![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() . 解得:
. 解得:![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
![]() .
.
∴![]() 点坐标为
点坐标为![]() 或
或![]() .…………………………7分
.…………………………7分
三、函数与应用
1. (大兴一模)某肉食加工厂在烤制风味肠时主要依据的是下面表格中的数据:
| 风味肠的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 烤制时间/分 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
根据以上表格所提供的信息回答:
⑴ 当烤制的风味肠的质量为2.5千克时,需要烤制时间是多少?
⑵ 当烤制的风味肠的质量为![]() 千克时,需要烤制时间是多少分钟?
千克时,需要烤制时间是多少分钟?
【答案】
⑴ 由表中提供的数据可知,当烤制的风味肠的质量为2.5千克时,
需要烤制时间是24分钟. ………………………………………………1分
⑵ 从表中可以看出,风味肠的质量每增加0.5千克,烤制风味肠的时间增加4分钟,由此可知烤制时间是风味肠的质量的一次函数.
设烤制时间为![]() 分钟,风味肠的质量为
分钟,风味肠的质量为![]() 千克,
千克,
![]() 与
与![]() 的一次函数关系式为:
的一次函数关系式为:![]() ……………………………………2分
……………………………………2分
由题意可得:![]() ,解得
,解得![]() ……………………………………3分
……………………………………3分
所以![]() ………………………………………………………………4分
………………………………………………………………4分
当![]() 千克时,
千克时,![]() .
.
所以当烤制的风味肠的质量为a千克时,需要烤制风味肠的时间是![]() 分钟……5分
分钟……5分
2.
(丰台一模)某公司专销产品![]() ,第一批产品
,第一批产品![]() 上市
上市![]() 天内全部售完.该公司对第一批产品
天内全部售完.该公司对第一批产品![]() 上市后的市场销售情况进行了跟踪调查,调查结果如图(1)和图(2)所示,其中图(1)中的折线表示的是市场日销售量
上市后的市场销售情况进行了跟踪调查,调查结果如图(1)和图(2)所示,其中图(1)中的折线表示的是市场日销售量![]() (万件)与上市时间
(万件)与上市时间![]() (天)的关系,图(2)中的折线表示的是每件产品
(天)的关系,图(2)中的折线表示的是每件产品![]() 的日销售利润
的日销售利润![]() (元)与上市时间
(元)与上市时间![]() (天)的关系.
(天)的关系.
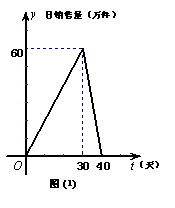

⑴ 试写出第一批产品![]() 的市场日销售量
的市场日销售量![]() (万件)与上市时间
(万件)与上市时间![]() (天)的关系式;
(天)的关系式;
⑵ 第一批产品![]() 上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?
上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?
【答案】⑴
①当![]() 时,设
时,设![]() ,
,
∵图象过点![]() ,
,
∴![]() ,解得,
,解得,![]() ,
,
∴![]() . ……………………………………………………………………
. ……………………………………………………………………![]() 分
分
② 当![]() 时,设
时,设![]() ,
,
∵图象过点![]() ,
,
∴![]() 解得,
解得,![]()
∴![]() .………………………………………………………………
.………………………………………………………………![]() 分
分
综上所述,![]() …………………………………
…………………………………![]() 分
分
⑵ 解法一:
由图⑴知,当t=30天时,日销售量最大为60万件; …………………![]() 分
分
由图⑵知,当t=30天时,产品的日销售利润最大为60元/件;………![]() 分
分
故当t=30天时,市场的日销售利润最大为![]() 万元.…………
万元.…………![]() 分
分
解法二:
由图⑵,得每件产品的日销售利润为![]() ,
,![]()
当![]() 时,产品的日销售利润为
时,产品的日销售利润为![]() ,此时利润最大为2400万元;
,此时利润最大为2400万元;
当![]() 时,产品的日销售利润为
时,产品的日销售利润为![]() ,此时利润最大为3600万元;
,此时利润最大为3600万元;
当![]() 时,产品的日销售利润为
时,产品的日销售利润为![]() ,此时利润最大为3600万元.
,此时利润最大为3600万元.
3.
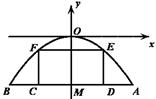 (丰台一模)有一座抛物线型拱桥,其水面宽
(丰台一模)有一座抛物线型拱桥,其水面宽![]() 为18米,拱顶
为18米,拱顶![]() 离水面
离水面![]() 的距离
的距离![]() 为8米,货船在水面上的部分的横断面是矩形
为8米,货船在水面上的部分的横断面是矩形![]() ,如图建立平面直角坐标系.
,如图建立平面直角坐标系.
⑴ 求此抛物线的解析式,并写出自变量的取值范围;
⑵ 如果限定![]() 的长为9米,
的长为9米,![]() 不能超过多少米,才能使船通过拱桥?
不能超过多少米,才能使船通过拱桥?
⑶ 若设![]() ,请将矩形
,请将矩形![]() 的面积
的面积![]() 用含
用含![]() 的代数式表示,并指出
的代数式表示,并指出![]() 的取值范围.
的取值范围.
【答案】⑴ 依题意可知,点![]() ,………………………………………………
,………………………………………………![]() 分
分
设抛物线的解析式为![]() ,∴
,∴![]() . ……………………………
. ……………………………![]() 分
分
![]() ,
,
自变量x的取值范围是![]() . …………………………………………
. …………………………………………![]() 分
分
⑵ ![]() ,
,
∴点![]() 的横坐标为
的横坐标为![]() ,则点
,则点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,……………………………………………………
,……………………………………………………![]() 分
分
因此要使货船能通过拱桥,则货船高度不能超过![]() (米).…………
(米).…………![]() 分
分
⑶ 由![]() ,则
,则![]() 点坐标为
点坐标为![]() ,…………………………
,…………………………![]() 分
分
此时 ![]() , ………………………………………
, ………………………………………![]() 分
分
∴![]() ,
, ![]() . …………………
. …………………![]() 分
分
4. (昌平二模)在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数S(次/分)是这个人年龄n(岁)的一次函数. 已知在正常情况下,年龄15岁和45岁的人在运动时所能承受的最高心跳次数分别为164次/分和114次/分.
⑴ 根据以上信息,求在正常情况下,S关于n的函数关系式;
⑵ 若一位63岁的人在跑步,医生在途中给他测得10秒心跳为26次,问:他是否有危险?为什么?
【答案】⑴ 设![]() .
.
由题设得
所以,S关于n的函数关系式为![]() ……………………3分
……………………3分
⑵ 当![]() 时,
时,![]() ,
,
因为这位63岁的人10秒心跳为26次,所以,每分钟心跳为156次,
因此,他不适合从事如此剧烈的运动,他有危险. ……………………5分
5. (昌平二模)五一期间,某区一中、二中组织100名优秀教师去某景区旅游,(其中一中教师多于二中教师),景区门票价格规定如下表:
| 一次性够票人数 | 1~49人 | 50~99人 | 100人以上 |
| 每人门票价格 | 50元 | 45元 | 40元 |
若两校都以校为单位一次性够票,则两校一共需付4725元,求两校各有多少名优秀教师参加这次旅游?若两校联合起来,作为一个团体够票,能节约多少钱?
【答案】设一中优秀教师![]() 人,则二中优秀教师
人,则二中优秀教师![]() 人,……………………1分
人,……………………1分
由题意得:![]() ……………………3分
……………………3分
解之,得![]() ,
,![]() ……………………4分
……………………4分
![]() (元)……………………5分
(元)……………………5分
∴一中、二中分别55名、45名优秀教师参加这次旅游,若两校联合起来够票,可节约725元.