九年级数学复习测试卷一
一、选择题：（36分）
1.下列关系式中，哪个等式表示
是
的反比例函数（
）
A：
B：
C：
D：
2.一个暗箱里装有10个黑球，8个白球，12个红球，每个球除颜色外都相同，从中任意摸出一球，摸到白球的概率是（ ） A：
B：
C：
D：
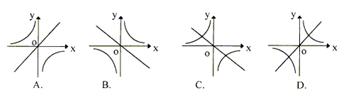
3．在同一平面直角坐标系中，正比例函数
与反比例函数
的图像大致位置不可能（ ）
4．如图，在矩形ABCD中，AB＝3，BC＝4，点P在BC边上运动，连结DP，过点A作AE⊥DP，垂足为E，设DP＝，AE＝，则能反映与之间函数关系的大致图象是（ ）
5．已知三点
，
，
都在反比例函数
的图象上，若
，
，则下列式子正确的是（ ）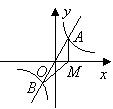
A．
B．
C．
D．
6．如图，直线
与双曲线交于点
．过点
作
轴，垂足为点
，连结
．若
，则
的值是（ ）
A．
B．
C．
D．
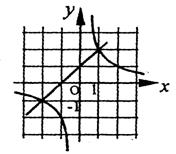7．如图，是一次函数y=kx+b与反比例函数的图像，则关于x的方程kx+b=
的解为( ) (A)xl=1，x2=2 (B)xl=-2，x2=-1
(C)xl=1，x2=-2 (D)xl=2，x2=-1
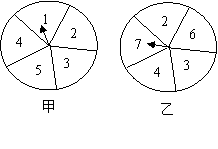
8．在如图右的甲、乙两个转盘中，指针指向每一个数字的机会是均等的．当同时转动两个转盘，停止后指针所指的两个数字表示两条线段的长，如果第三条线段的长为5，那么这三条线段不能构成三角形的概率是（ ）
A．
B．
C．
D．
9． 边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴, 反比例函数与
的图象均与正方形ABCD的边相交,则图中的阴影部分的面积是( )
A、2 B、4 C、8 D、6
10.已知点A（-1，5）在反比例函数
的图象上，则该函数的解析式为（ ）A：
B：
C：
D：
11.三角形两边的长分别是8和6，第三边的长是一元二次方程
的一个实数根，则这个三角形的面积是（
）
A：24
B：24或
C：48
D：
12.若反比例函数经过（-2，3），则这个反比例函数一定经过（
）
A：（-2，-3） B：（3，2） C：（3，-2） D：（-3，-2）
10.在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致为
|
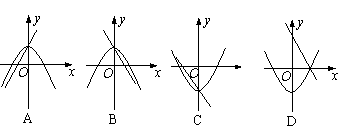
二、填空题：(每题3分,共36分)
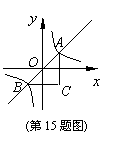
13.如图，反比例函数
的图象与直线
相交于A,B两点，
AC∥轴，BC∥轴，则△ABC的面积等于___________个面积单位.
14．将正整数按如图所示的规律排列下去。若用有序实数对（
，）表示第排，从左到右第个数，如（4，3）表示实数9，则（7，2）表示的实数是
___________。
16．将分别标有数字1，4，8的三张卡片洗匀后，背面朝上放在桌面上。随机地抽取一张作为十位上的数 字（不放回），再抽取一张作为个位上的数字，能组成两位数恰好是“18”的概率为_________.
17．三名同学同一天生日，她们做了一个游戏：买来3张相同的贺卡，各自在其中一张内写上祝福的话，然后放在一起，每人随机拿一张．则她们拿到的贺卡都不是自己所写的概率是__________
18.已知抛物线
的对称轴为
，且经过点(1,4)和点(5,0)，则该抛物线的解析式为 ___________________ ；
19.在△ABC中,∠C=900,AC=3, AB=5,则cos B=____________。
20.已知Rt△ABC中，∠C=90度，sinA=
，则
_______________ 。
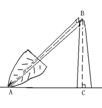
21.如图，在一次龙卷风中，一棵大树在离地面若干米处折断倒下，B为折断处最高点，树顶A落在离树根C的12米处，测得∠BAC=300，则BC的长是______________米。
22.若∠A是锐角，cosA＝
，则∠A＝____________ 。
23.计算2sin30°+3tan30° ·tan45°=___________。
24.如图，在坡度为1︰2的山坡上种树，要求株距（相邻两树间的水平距离）是6米，斜坡上相邻两树间的坡面距离是_________ 米．
三、解答题：(60分)
21． （本题满分10分） 小明和小颖玩掷硬币的游戏，游戏规则如下：
将一枚均匀硬币任意掷两次，两次都是正面朝上小明赢，否则小颖赢，
这是一个对游戏双方都公平的游戏吗？试说明理由。如果你认为这个游
戏不公平，请你为小明和小颖设计一个公平的游戏规则。
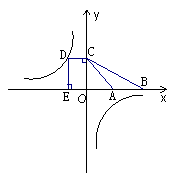23．（本题10分）D为反比例函数：
图象上一点.过D作DC⊥y轴于C, DE⊥x轴于E,一次函数
与
的图象都过C点,与x轴分别交于A、B两点。若梯形DCAE的面积为4，求k的值.
23．(6分)已知一个二次函数的图象经过点(0，0)，(1，—3)，(2，—8).
求这个二次函数的解析式；
写出它的对称轴和顶点坐标。
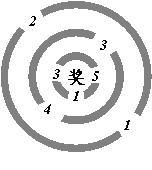
27．（本题10分）某学校七年级数学兴起小组组织一次数学活动。在一座有三道环形路的数字迷宫的每个进口处都标记着一个数，要求进入者把自己当做数“1”，进入时必须乘进口处的数，并将结果带到下一个进口，依次累乘下去，在通过最后一个进口时，只有乘积是5的倍数，才可以进入迷宫中心。现让一名5岁小朋友小军从最外环任一个进口进入。
(1)小军能进入迷宫中心的概率是多少？请画出树状图进行说明；
(2)小组两位组员小张和小李商量做一个小游戏，以猜测小军进迷宫的结果比胜负。游戏规则规定：小军如果能进入迷宫中心，小张和小李各得1分；小军如果不能进入进入迷宫中心。则他在最后一个进口处所得乘积是奇数时，小张得3分，所得乘积是偶数时，小李得3分。你认为这个游戏公平吗？如果公平，请说明理由；如果不公平，请在第二道环进口处得两个数中改变其中一个数使游戏公平；
(3)在(2)的游戏规则下，让小军从最外环进口任意进入10次，最终小张和小李的总得分之和不超过28分，请问小军至少几次进入迷宫中心？
28.（12分）如图，一位篮球运动员跳起投篮，球沿抛物线
运行，然后准确落入篮框内．已知篮框的中心离地面的距离为3.05米．
（1）球在空中运行的最大高度为多少米？
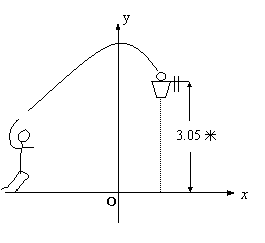（2）如果该运动员跳投时，球出手离地面的高度为2.25米，请问他距离篮
框中心的水平距离是多少？