九年级数学复习测试卷二
一、选择题 （每题3分，共60分）
1.口袋中放有3个黄球和3个黑球,每个球除颜色外都相同.从中任意摸出两个球,则一个是黄球,一个是黑球的概率是 ：（ ）A. 
B. 
C. 
D. 
3.已知,如图,A,B两村之间有三条道路,甲,乙两人分别从A,B两村同时出发,他们途中相遇的概率为 ：（ ）A、 
B 、
C、 
D、
2．准备两张大小一样，分别画有不同图案的正方形纸片，把每张纸都对折、剪开，将四张纸片放在盒子里，然后混合，随意抽出两张正好能拼成原图的概率是：
A.
B.
C.
D.
3．中央电视台“幸运52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标牌中，有5个商标牌的背面注明一定的奖金额，其余商标的背面是一张哭脸，若翻到哭脸就不得奖金，参与这个游戏的观众有三次翻牌的机会(翻过的牌不能再翻)。某观众前两次翻牌均获得若干奖金，那么他第三次翻牌获奖的概率是：（ ）A. B. C.
D.
4．在同一直角坐标平面内，如果
与
没有交点，那么
和
的关系一定是：
A.<0，>0 B.>0，<0
C.、同号 D.、异号
5．某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上标志，然后放回，待有标志的黄羊完全混合于黄羊群后，第二次捕捉60只黄羊，发现其中2只有标志。从而估计该地区有黄羊：
A．400只 B. 600只 C. 800只 D. 1000只
6．如图，两个同心圆中，大圆的半径是小圆半径的2倍，把一粒
大米抛到圆形区域中，则大米落在小圆内的概率为（ ）
A． 
B．
C． 
D．无法确定
7．如图1，在Rt△ACB中，∠ C = 90°，则 sin A = （ ）
A、
，B、
，C、
，D、
.
8．在Rt△ACB中，∠ C = 90°，下列式子成立的是（ ）
A、a = c sin B, B、a = b cos B , C、c = a sin B , D、a = b tan A .
9．在Rt△ACB中，若 tan A = 
，则锐角∠A = （ ）
A、30°，B、45°，C、60°，D、不能确定.
10．2cos 45°的值等于（ ）
A、1 ，B、
，C、 ，D、2 .
11．已知α为锐角且tan （90°－α）= ，则α= （ ）
A、30°，B、45°，C、60°，D、不能确定.
12．在Rt△ACB中，∠ C = 90°，若sin A = 
，则tan B =( )
A、，B、
，C、
，D、
.
13．在Rt△ABC中，∠C = 90°，AB = 10 ，BC = 8 ，则cos A = （ ）
A、
，B、
，C、
，D、
.
14．掷一枚均匀的硬币两次，两次均为反面朝上的概率是（ ）
A、
，B、
，C、，D、
.
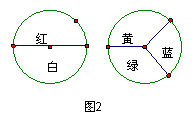15．利用如图2的两个转盘进行“配紫色”的游戏，能配得紫色的概率是（ ）
A、，B、，C、
，D、
.
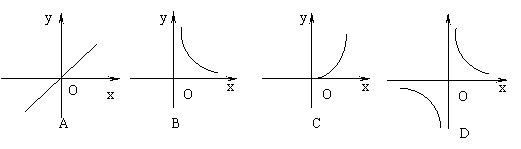
16．甲、乙两地相距60km，则汽车由甲地行驶
到乙地所用时间y（小时）与行驶速度x（千米/时）之间的函数图像大致是（ ）
17． 在△ABC中，已知AC=3，BC=4，AB=5，那么下列结论成立的是
A.sinA
=
B.cosA =
C.tanA =
D.sinB =
18．用配方法将二次函数y= x²-2x+1写成y=a(x-h)²+k的形式是（
）
A．y= (x-2)²-1 B．y= (x-1)²-1
C．y= (x-2)²-3 D、y= (x-1)²-3
19．把抛物线y=－2x2的图象向左平移4个单位，再向上平移3个单位，所得的图象的表达式（ ）
A．y=－2（x＋4）2＋3 B．y=－2（x－4）2－3
C．y=－2（x＋4）2－3 D．y=－2（x－4）2＋3
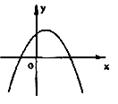20.
已知二次函数
的图象如图所示，
则下列结论正确的是
（ ）
A．
B．
C．
D．
二、填空题 ( 每空2分，共22分 )
21．反比例函数
的图象经过点P（
，
），且为是一元二次方程
的两根，那么点P的坐标是________ _
22．在函数
（
为常数）的图象上有三个点（-2，
），(-1，
)，（，
），函数值，，的大小关系为
；
23． 已知点P（1，）在反比例函数
的图像上，其中
(
为实数)，则这个函数的图像在第_______ 象限；
24．一个密码锁的密码由四个数字组成，每个数字都是0～9这十个数中的一个，李阿姨忘记了开头和结尾共两个数字，她一次就能打开该锁的概率是
25．(1)计算：6 tan 
30°－ sin 60°－2 cos 45°=___________.
(2)计算： （－ 2 ） － 4 sin 60°+ 
=____________ .
26.已知二次函数y=x2＋bx＋c，其图象的顶点为（5，－2则b= ，c= ．
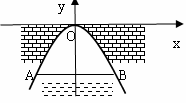27．如图，某涵洞的截面是抛物线形，现测得水面宽是AB=1.6m,涵洞顶点O到水面的距离CO为2.4m,在图中直角坐标系内，涵洞截面所在抛物线的解析式是
。
28．将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖
20个，若这种商品零售价在一定范围每降价1元，其销售量就增加1个，
为获得最大利润，应降价 元.
29．若抛物线y=2x2－4x+1与x轴两交点分别是(x1，0)，(x2，0)，则
x12+x22=______.
四、解答题（30题6分，31题10分，32题8分，33题8分，34题6分）
30．利用树状图求：把一枚均匀的硬币连续抛掷三次，“至少有一个硬币是正面朝上” 的概率。
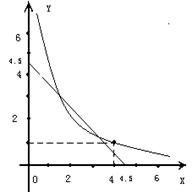31. 探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（继续完成下列探索过程）
（1） 小明是这样探索的：如果矩形A的边长为m和n。
那么设所求矩形B的两边分别是
，由题意得：
（2）如右图，在同一平面直角坐标系中画出了一次函数
和反比例函数的部分图象，其中x和y分别表示矩形B
的两边长，请你结合刚才的研究，回答下列问题：
（i）这个图象所研究的矩形A的两边长为___ __和__ ___;
（ii）满足条件的矩形B的两边长为___ __和___ __.
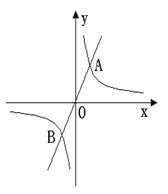32．如图，已知正比例函数y=kx的图象与反比例函数y=
的图象相交于A、B两点，且A点的横坐标为2。
（1）求A、B两点的坐标；
（2）在x轴上取关于原点对称的P、Q两点，（P点在Q点的右边），试问
（3）四边形AQBP一定是一个什么形状的四边形？并说明理由；
（4）上述四边形AQBP能否为矩形？若能，请求出点P、Q的坐标和矩形AQBP
的面积；若不能，请说明理由。
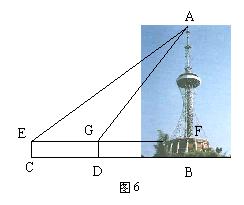
33．如图6，在测量塔高AB时选择与塔底在同一水平面的同一直线上的C、D两点，用测角仪测得塔顶A 的仰角分别是30°和60°，已知测角仪高CE = 1.5米，CD = 30米，求塔高AB（答案保留根号） .
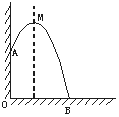
1934．某幢建筑物，从10 m高的窗口A，用水管向外喷水，喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直，如图，如果抛物线的最高点M离墙1
m，离地面
m，
（1）在图形中建立适当的直角坐标系，求出水流呈抛物线的解析式；
（2）则水流落地点B离墙的距离OB是多少?