![]() 九年级数学月考(12月)测试题
九年级数学月考(12月)测试题
(满分:100分;考试时间:120分钟)
命题人:刘淑莉
|
| 一 | 二 | 三 | 总 分 |
| 得分 |
|
|
|
|
一、填空题:(每空1分,共67分)
1.在![]() 中,已知
中,已知![]() ,则
,则![]() 。
。
2.如果sinα=![]() ,则锐角α的余角是__________.
,则锐角α的余角是__________.
3.已知:∠A为锐角,且sinA=![]() ,则tanA的值为__________.
,则tanA的值为__________.
4.等腰直角三角形的一个锐角的余弦值等于 。
5.若![]() 是锐角,
是锐角,![]() ,则
,则![]() 。
。
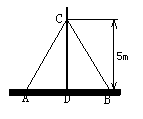
6.如图(见背面),在离地面高度为5m的C处引拉线固定电线杆,拉线与地面成α角, 则拉线AC的长为__________m(用α的三角函数值表示).
7. 在离旗杆20m的地方用测角仪测得旗杆杆顶的仰角为α,如果测角仪高1.5m, 那么旗杆高为_____ ___m.
8. 一个小球由静止开始在一个斜坡上向下滚动, 通过仪器观察得到小球滚动的距离s(m)与时间t(s)的数据如下表:
| 时间t(s) | 1 | 2 | 3 | 4 | … |
| 距离s(m) | 2 | 8 | 18 | 32 | … |
已知小球滚动的距离s是时间t的二次函数,则s与t的函数表达式为_________.
9.函数y=(2k+1)x![]() -3x+k中,当k 时,图象是直线,当k
时,图象是抛物线;当k 时,抛物线经过原点。
-3x+k中,当k 时,图象是直线,当k
时,图象是抛物线;当k 时,抛物线经过原点。
10.已知二次函数y=(2a+1)x![]() 的开口向下,则a的取值范围是
的开口向下,则a的取值范围是
11.函数y=![]() 是二次函数,当a =_____时,其图象开口向上;当a =_____时,其图象开口向下.
是二次函数,当a =_____时,其图象开口向上;当a =_____时,其图象开口向下.
12.已知函数y=-![]() x
x![]() ,则其图象开口向 ,对称轴为 ,顶点坐标为
,当x≥0时,y随x的增大而
,则其图象开口向 ,对称轴为 ,顶点坐标为
,当x≥0时,y随x的增大而
13.抛物线y=-![]() x
x![]() -3的图象开口 ,对称轴是
,顶点坐标为
,当x= 时,y有最 值为
-3的图象开口 ,对称轴是
,顶点坐标为
,当x= 时,y有最 值为
当x=0时,函数y的值最大,最大值是 ,当x 0时,y<0。
14.抛物线y=3x![]() +4可以由抛物线y=3x
+4可以由抛物线y=3x![]() 沿 平移
得到;同样,y=3x
沿 平移
得到;同样,y=3x![]() -4可以由抛物线y=3x
-4可以由抛物线y=3x![]() 沿 平移
得到
沿 平移
得到
15.抛物线y=3(x-1) ![]() 的开口方向 ,对称轴为 ,顶点坐标是
的开口方向 ,对称轴为 ,顶点坐标是
16.对于形如y=a(x-h)![]() +k的抛物线,当a 时,开口向上,当a 时,开口向下,它的对称轴是直线
,顶点坐标是
+k的抛物线,当a 时,开口向上,当a 时,开口向下,它的对称轴是直线
,顶点坐标是
17.二次函数y=![]() x
x![]() -x-3写成y=a(x-h)
-x-3写成y=a(x-h)![]() +k的形式后,h= ,k= 。
+k的形式后,h= ,k= 。
18.把函数y=-x![]() -4x-5配方得
,它的开口方向 ,顶点坐标是
,对称轴是 ,最高点是
-4x-5配方得
,它的开口方向 ,顶点坐标是
,对称轴是 ,最高点是
19.抛物线y=-2x![]() +6x-1的顶点坐标为
,对称轴为
+6x-1的顶点坐标为
,对称轴为
20.已知二次函数y=![]() x
x![]() -
-![]() x+6,当x= 时,y
x+6,当x= 时,y![]() = ;当x 时,y随x的增大而减小。
= ;当x 时,y随x的增大而减小。
21.抛物线y=3x![]() +bx+c的顶点坐标为(
+bx+c的顶点坐标为(![]() ,0),则b=
,c=
,0),则b=
,c=
22.抛物线y=2x![]() 的图象向左平移1个单位,再向下平移3个单位,得到的抛物线表达式为
的图象向左平移1个单位,再向下平移3个单位,得到的抛物线表达式为
23.y=(x-1)2-2可由 的图象向右平移1个单位,再向下平移2个单位得到。
24.二次函数y=![]() x
x![]() +3x+
+3x+![]() 的图象是则函数y=
的图象是则函数y=![]() x
x![]() 的图象先向 平移 个单位,再向 平移 个单位得到的。
的图象先向 平移 个单位,再向 平移 个单位得到的。
25.已知二次函数y=ax![]() +bx+c(a≠0)的图象如图所示,则a+b+c 0。(填“>”“<”或“=”;26、27题同)
+bx+c(a≠0)的图象如图所示,则a+b+c 0。(填“>”“<”或“=”;26、27题同)
26.二次函数y=ax![]() +bx+c的图象如图所示,则a 0,b 0,c 0
+bx+c的图象如图所示,则a 0,b 0,c 0
27.二次函数y=ax![]() +bx+c的图象如图所示,则ac 0。
+bx+c的图象如图所示,则ac 0。
28.已知,抛物线y=ax![]() +c与抛物线y=-2x
+c与抛物线y=-2x![]() -1关于x轴对称,则a=
,c=
-1关于x轴对称,则a=
,c=
29.已知抛物线y=ax![]() 与直线y=kx+1交于A、B两点,其中A点坐标是(1,4),则a= ,k=
,B点坐标是
与直线y=kx+1交于A、B两点,其中A点坐标是(1,4),则a= ,k=
,B点坐标是
30.已知抛物线y=ax![]() +x+c与x轴交点的横坐标为-1,则a+c=
+x+c与x轴交点的横坐标为-1,则a+c=
31.已知二次函数y=x![]() -2(m-1)x+m
-2(m-1)x+m![]() -2m-3的图象与函数y=-x
-2m-3的图象与函数y=-x![]() +6x的图象交于y轴上一点,则m=
+6x的图象交于y轴上一点,则m=
![]()
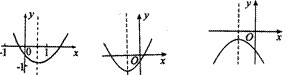
 第25题 第26题 第27题
第25题 第26题 第27题
第6题
二、选择题:(每小题1分,共3分)
32.在直角三角形ABC中,如果各边长度都缩小2倍,则锐角A的正弦值和正切值( )
A.都缩小2倍 B.都扩大2倍; C.都没有变化 D.不能确定
33、已知甲、乙两坡的坡角分别为α、β, 若甲坡比乙坡更陡些, 则下列结论正确是( )
A.tanα<tanβ B.sinα<sinβ; C.cosα<cosβ D.cosα>cosβ
34.一辆汽车沿坡角为α的斜坡前进500米,则它上升的最大高度为( )
A.500sinα B.![]() C.500cosα D.
C.500cosα D.![]()
三、解答题:(共30分)
35.(8分)计算
⑴、![]() ⑵、
⑵、![]()
⑶、![]() ⑷、
⑷、![]()
![]() 36.(4分)如图,在
36.(4分)如图,在![]() 中,
中,![]() ,
,![]() 是中线,
是中线,![]() ,求
,求![]() 和
和![]() 。
。
 | |||
 | |||
37.(4分)一艘船由A港沿东偏北![]() 方向航行20千米至B港,然后再沿南偏东
方向航行20千米至B港,然后再沿南偏东![]() 方向航行20千米至C港,求:
方向航行20千米至C港,求:
(1)A,C两港之间的距离(结果精确到![]() 千米,参考数值
千米,参考数值![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
(2)确定C港在A港的什么方位?
38.(4分)已知抛物线y=ax![]() (a≠0)与直线y=-2x+3交于点(-1,b)
(a≠0)与直线y=-2x+3交于点(-1,b)
(1)求a、b的值;
(2)求抛物线与y=x+6的两交点及顶点所构成的三角形的面积。
39.(6分)心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间满足函数关系y=-0.1x2+2.6x+43(0≤x≤30).y值越大,表示接受能力越强.
(1)x在什么范围内,学生的接受能力逐步增强?x在什么范围内,学生的接受能力逐渐降低?
(2)第10分时,学生的接受能力是多少?
(3)第几分时,学生的接受能力最强?
40.(6分)某船以每小时36海里的速度向正东航行,在A点测得某岛C在北偏东600方向上,航行半小时后到B点,测得C岛在北偏东300方向上,已知该岛周围16海里内有暗礁
(1)试说明B点是否在暗礁区域外
(2)若船继续向东航行,有无触礁危险,请说明理由。