数 学 试 卷
| 题号 | 一 | 二 | 三 | 四 | 五 | 总分 | |||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||||||||
（说明：全卷共8页，考试时间90分钟，满分120分）
一．选择题（本题共5小题，每小题3分，共15分，每小题给的四个答案中，有且只有一个是正确的，将你认为正确的选项填在题后的括号内）
1．3的相反数是（ ）
A．-3 B．
C．
D．3
2．已知圆的半径为5cm，圆心到弦的距离为4cm，那么这条弦长是（ ）
A．3cm B．6cm C． 8cm D．10cm
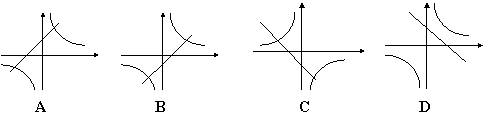3．在同一坐标系中，函数
和
的图象大致是（ ）
4．图1中几何体的主视图是（ ）
5．如图2，在△ABC中，∠C=90°，AC=8cm，AB的垂直平分线MN交AC于
D，连结BD，若cos∠BDC=
，则BC的长是（ ）
A． 4cm B． 6cm
C． 8cm D． 10cm
二．填空题（本题共5小题，每小题4分，共20分，请把你认为正确的答案写在横线上）
6．分解因式：ab2 －2ab ＋ a ＝
．
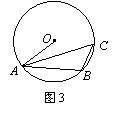
7．如图3，A，B，C为⊙O上的三点，如果∠OAB＝48°，
则∠ACB＝ ．
8．若关于x的一元二次方程 x2 －3x ＋ m = 0有实数根，
则m的取值范围是
．
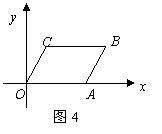
9．如图4，在平面直角坐标系中，□OABC的顶点
O 、A 、C 的坐标分别是（0 ，0）、（5 ，0）、
（2 ，3）则顶点B的坐标是
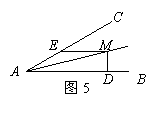10．如图5，∠BAC＝30°，AM是∠BAC的平分线，
过M作ME∥BA交AC于E，作MD⊥BA，
垂足为D，ME＝10cm，则MD＝________．
三．解答题（本题共5小题，每小题6分，共30分）
11．解方程组
12．求抛物线y＝x2＋4x＋3的对称轴、顶点坐标和与x轴的交点坐标．
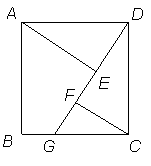13．如图所示，四边形ABCD是正方形，G是BC上任意一点（点G与B、C不重合），
AE⊥DG于点E，CF∥AE交DG于点F．
（1）在图中找出一对全等三角形，并加以证明．
（2）求证：AE＝FC＋EF．
14．甲、乙、丙三人相互传球，由甲先发球，传给下一人作为第一次传球．
（1）用列表或画树状图的方法表示经过3次传球后的所有可能结果．
（2）求经过第3次传球后，球仍回到甲手中的概率．
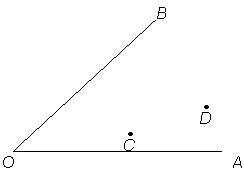
15．如图，用尺规作图的方法求作一点P，使PC=PD，并且P到∠AOB两边的
距离相等．（保留作图痕迹，不要求写作法、证明）
四．（本题共4小题，每小题7分，共28分）
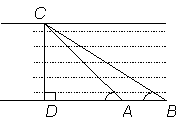16．在数学活动课上，老师带领学生去测河宽，某学生在点A处观测到河对
岸水边处有一点C，并测得∠CAD = 45o，在距离A点30m的B处测得
∠CBD=30o．求河宽CD．（结果可带根号）
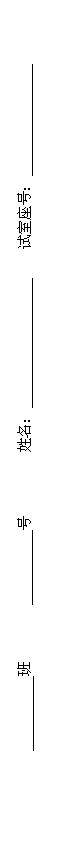
17．如图，直线
与双曲线
只有一个交点
，且与
轴，
轴分
别交于B，C两点，
垂直平分OB，垂足为D，求直线与双曲线的解析式．
18．某工人要制造180个相同零件，在制造完40个零件后，他改进技术每天多制造
15个零件，恰好共用6天全部完成，问该工人改进技术后每天制造多少个零件？
19．某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类.在“深圳读书月”活动期间，为了解图书的借阅情况，图书管理员对本月各类图书的借阅量进行了统计，图8-1和图8-2是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图．请你根据图表中提供的信息,解答以下问题:
| 频率分布表 | ||
| 图书种类 | 频数 | 频率 |
| 自然科学 | 400 | 0.20 |
| 文学艺术 | 1000 | 0.50 |
| 社会百科 | 500 | 0.25 |
| 数学 | ||
图8-1
（1）填充图8-1频率分布表中的空格．
（2）在图8-2中，将表示“自然科学”的部分补充完整．
（3）若该学校打算采购一万册图书,请你估算“数学”类图书应采购多少册较合适？
五．解答题（本题共3小题，每小题9分，共27分）
20．工艺商场按标价销售某种工艺品时，每件可获利45元；按标价的八五折销
售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
（1）该工艺品每件的进价、标价分别是多少元？
（2）若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工
艺品100件．若每件工艺品降价1元，则每天可多售出该工艺品4件．问每件工
艺品降价多少元出售，每天获得的利润最大？获得的最大利润是多少元?
21．如图，点P是菱形ABCD的对角线BD上一点，连结CP并延长，交AD于E，交BA的延长线于点F．
问：(1) 图中△APD与哪个三角形全等？试证明之．
(2) 试证明△APE ∽△FPA．
(3) 猜想：线段PC、PE、PF之间存在什么关系？说明理由．
 |
22．如图，以知二次函数的图象的顶点坐标为C（1，0），直线y = x ＋
m与该二次函
数的图象交于A、B两点，其中A点的坐标为（3，4），B点在y轴上．
（1）求m的值及这个二次函数的关系式；
（2）P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二
次函数的图象交与E点，设线段PE的长为h，点P的横坐标为x，求h与x之间
的函数关系式，并写出自变量x的取值范围；
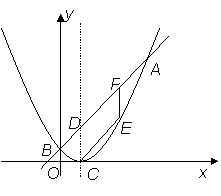（3）D为直线AB与这个二次函数的图象对称轴的交点，在线段AB上是否存在一点P，
使得四边形DCEP是平行四边形？若存在，请求出此时P点的坐标；若不存在，
请说明理由．