相似三角形的性质和判定测试
姓名 得分
一、 认真填一填(每空3分,共30分)
1、一公园占地面积约为800000
，若按比例尺1∶2000缩小后，其面积约为
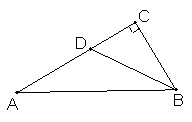
2、如图，要使ΔABC∽ΔACD，从边的角度，需补充的条件是 ．
3、已知ΔABC∽ΔA′B′C′，且BC∶B′C′＝AC∶A′C′，若AC＝1，A′C′＝2，则ΔA′B′C′与ΔABC的相似比是 ．
4、已知ΔABC∽ΔA′B′C′，ΔABC的周长是20cm，ΔA′B′C′的周长是12cm，ΔABC的最长边为8cm，则ΔA′B′C′的最长边是 cm．
5、如图，P是ΔABC的边AB上一点，若ΔAPC∽ΔABC，，则∠1＝∠ ．
6、在ΔABC中，AB＝4，BC＝9，AC＝8，在AC上取一点M，当AM的长为 时，
ΔAMB∽ΔABC．
（第9题） （第11题）
7、已知AD为Rt△ABC斜边BC上的高，且AB=15cm，BD=9cm，则AD= ，CD= 。
8、若△ABC∽△A′B′C′，且
，△ABC的周长为12cm，则△A′B′C′的周长为
；若△ABC的面积为18cm2,则△A′B′C′的面积为
cm2。
二、仔细选一选 (每题3分,共30分)
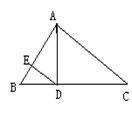
9、如图，在Rt△ABC中，AD⊥BC与D，DE⊥AB与E，若AD=3，DE=2，则AC= （ ）
A、
B、
C、
D、
10、下列三角形中，一定相似的是 （ ）
A．两个等腰三角形 B．两个直角三角形 C．两个等边三角形 D．两个钝角三角形
11、如图，AD⊥BC于点D，BE⊥AC于点E，则图中相似三角形的对数是（ ）
A．3对 B．4对 C．5对 D．6对
12、下列说法中不正确的是 （ ）
A．有一个角是30°的两个等腰三角形相似；B．有一个角是60°的两个等腰三角形相似；
C．有一个角是90°的两个等腰三角形相似；D．有一个角是120°的两个等腰三角形相似；
13、下列说法不正确的是 （ ）
A、 两对应角相等的三角形是相似三角形；
B、两对应边成比例的三角形是相似三角形；
C、三边对应成比例的三角形是相似三角形；
D、以上有两个说法是正确。
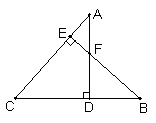
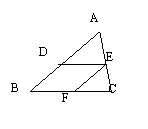
14、如图，DE∥BC，EF∥AB，则图中相似三角形有 （ ）
A、2对 B、3对 C、4对 D、5对
 |  | ||
(第14题) (第15题) (第16题) (第17题)
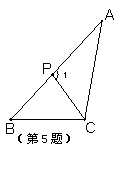
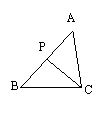
15、如图，若P为△ABC的边AB上一点（AB>AC），则下列条件不一定能保证△ACP∽△ABC的有 （ ）
A、∠ACP=∠B B、∠APC=∠ACB C、
D、
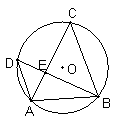
16、如图，已知ΔABC和ΔABD都是⊙O的内接三角形，AC和BD相交于点E，则与ΔADE相似的三角形是 （ ）
A．ΔBCE B．ΔABC C．ΔABD D．ΔABE
17、如图，RtΔABC中，∠C＝90°，D是AC边上一点，AB＝5，AC＝4，若ΔABC∽ΔBDC，
则CD＝ ( )
A．2 B．
C．
D．
18、已知D、E为△ABC的边AB、AC上的两点，且AB=8，AC=6，AD=4，AE=3，则
∶
=（
）
A、1∶2 B、1∶4 C、1∶3 D、2∶5
三、完整解一解 (每题10分,共60分)
19、已知∠A=∠D,AD、BC交于点O。
（1）、试说明△AOB∽△DOC。
（2）、若AO＝2，DO＝3，CD＝5，求AB的长。
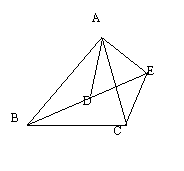20如图，
．
求证：（1）∠BAD＝∠CAE． （2）ΔABD∽ΔACE．
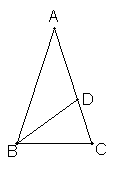
21如图，在ΔABC中，AB＝AC，∠A＝36°，BD是角平分线．
求证：（1）ΔABC∽ΔBCD； （2）BC是CD与CA的比例中项．
22某人利用树影长测树高。他在某一时刻测得长为1米的竹竿影长为0.9米，在同一时刻，他测得树影子长为2.7米，求树高。
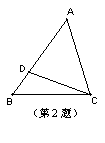
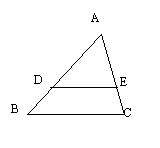
23已知，如图， 在△ABC中，DE∥BC，AD=5，BD=3，求S△ADE：S△ABC的值。（8分）
 |
四、作图：
24已知线段AB，求作一点P，使点P分AB成定比3∶4。
A ________________ B