九（上）第二十三章旋转章节测试
班级_____________ 学号__________ 姓名_________ 成绩评定________
一、 看准了再选
1．下列各图中，不是中心对称图形的是（ ）
2．在下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
3．如图，该图形围绕自己的旋转中心，按下列角度旋转后，不能与其自身重合的是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
 |
（第3题） （第4题）
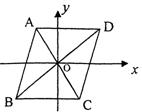4．如图，已知□ABCD的两条对角线AC与BD交于平面直角坐标
系的原点，点A的坐标为(-2，3)，则点C的坐标为( )
A．(-3，2) B.(-2，-3) C.(3，-2) D.(2，-3)
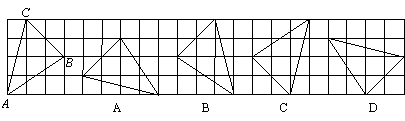
5． 在下图右侧的四个三角形中，不能由△ABC经过旋转或平移得到的是（ ）
 |
6．4张扑克牌如图（1）所示放在桌子上，小新把其中一张旋转180°后得到如图（2）所示，那么他所旋转的牌从左起是（ ）
A．第一张、第二张 B．第二张、第三张C．第三张、第四张 D．第四张、第一张
 |
（1） （2）
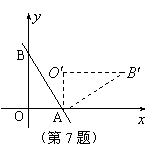
7．如图，直线
与
轴、
轴分别交于
、
两点，把△
绕点顺时针旋转90°后得到△
，则点
的坐标是
A. （3，4） B. （4，5） C. （7，4） D. （7，3）
 | |||||
 |  | ||||
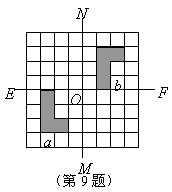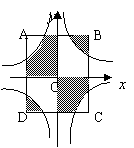（第8题）
8．如图，边长为4的正方形ABCD的对称中心是坐标原点O，AB∥轴，
BC∥轴，反比例函数
与
的图像均与正方形ABCD的边相交，则图中阴影部分的面 积之和是（ ）
A．2 B．4 C．6 D．8．
9. 已知坐标平面上的机器人接受指令“[a，A]”(a≥0，0°<A<180°)后的行动结果为：在原地顺时针旋转A后，再向面对方向沿直线行走a. 若机器人的位置在原点，面对方向为y轴的负半轴，则它完成一次指令[2，60°]后，所在位置的坐标为( )
A.
(-1，-
) B.
(-1，) C.(，-1) D.(-，-1)
10．如图，
方格纸的两条对称轴
相交于点
，对图
分别作下列变换：
①先以直线
为对称轴作轴对称图形，再向上平移4格；②先以点为中心旋转
，再向右平移1格；③先以直线
为对称轴作轴对称图形，再向右平移4格，其中能将图变换成图
的是（ ）
A．①② B．①③ C．②③ D．③
11．如图，在等边
中，
，点在
上，且
，点
是
上一动点，连结
，将线段绕点逆时针旋转
得到线段
．要使点
恰好落在
上，则
的长是（ ）
A．4 B．5 C．6 D．8
12．如图，
和
都是等腰直角三角形，
，四边形
是平行四边形，下列结论中错误的是（ ）
A．
以点为旋转中心，逆时针方向旋转
后与
重合
B．
以点为旋转中心，顺时针方向旋转
后与
重合
C．沿
所在直线折叠后，与
重合
D．沿
所在直线折叠后，与重合
 | |||
 | |||
（第12题） （第13题）
二、 想好了再填
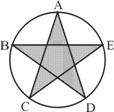
13．如图是中国共产主义青年团团旗上的图案（图案本身没有字母）则至 少旋转____________度后能与原来图形重合．
14．如果点
和点
关于原点对称，则点Q为
．
15．如图，一块等腰直角的三角板
，在水平桌面上绕点
按顺时针方向旋转到
的位置，使
三点共线，那么旋转角度的大小为 ．
16．下午2点30分时，时钟的分针与时针所成角的度数为___________.
17．如图，△ABC中，∠BAC＝90°，AB＝AC，
△ABC按逆时针方向旋转一个角度后，成为△ACD，则图中的____________是旋转中心，旋转角是___________。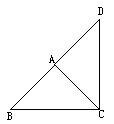
（第17题） （第18 题）
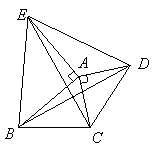
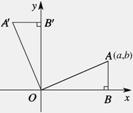
18．如图，将△AOB绕点O逆时针旋转90o，得到△A/OB/．若点A的坐标为（，），则点A/的坐标为__________．
19．如图用等腰直角三角板画
，并将三角板沿
方向平移到如图所示的虚线处后绕点
逆时针方向旋转
，则三角板的斜边与射线
的夹角
为______
．
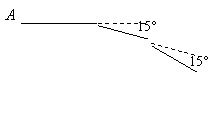
20．如图，小新从点出发前进
，向右转
，再前进，又向右转，…，这样一直走下去，他第一次回到出发点时，一共走了
m．
 |
三．想好了再规范的写画
21．如图所示，方格纸中的每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，
①把△ABC向上平移5个单位后得到对应的△A1B1C1，画出△A1B1C1，
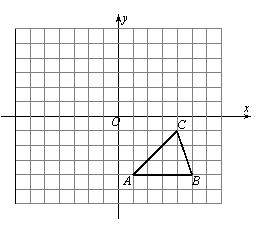②以原点O为对称中心，再画出与△A1B1C1关于原点O对称的△A2B2C2，。
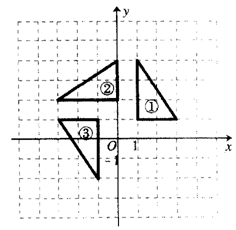
22．如图，在平面直角坐标系中，三角形②、③是由三角形①依次旋转后所得的图形．
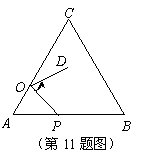
（1）在图中标出旋转中心P的位置，并写出它的坐标；
（2）在图上画出再次旋转后的三角形④．
23．如图是
正方形网格，请在其中选取一个白色的单位正方形并涂黑，使图中黑色部分是一个中心对称图形．
四．想好了再规范的写
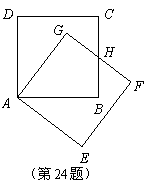
24．把正方形绕着点，按顺时针方向旋转得到正方形
，边
与交于点
（如图）．
（1）试问线段
与线段
相等吗？请先观察猜想，然后再证明你的猜想．
 |
（2）若正方形的边长为
，重叠部分（四边形ABHG）的面积为
，求旋转的角度．
25．一位同学拿了两块
三角尺
，做了一个探究活动：将 的直角顶点放在的斜边的中点处，设
．
 |
（1）如图（1），两三角尺的重叠部分为
，则重叠部分的面积为 ，周长为 ．
（2）将图（1）中的绕顶点逆时针旋转，得到图26（2），此时重叠部分的面积为
，周长为
．
（3）如果将绕旋转到不同于图（1）和图（2）的图形，如图（3），请你猜想此时重叠部分的面积为
．
（4）在图（3）情况下，若
，求出重叠部分图形的周长．
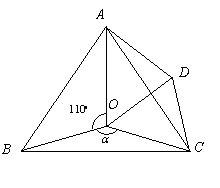
26．如图，点是等边内一点，
．将
绕点按顺时针方向旋转得
，连接．
（1）求证：
是等边三角形；
（2）当
时，试判断
的形状，并说明理由；
（3）探究：当为多少度时，是等腰三角形？