九年级一元二次方程测试
数学试卷
考号：_________姓名：________得分：_________
一、选择题（每题3分，共10题）
1.下列方程中，关于x的一元二次方程有（ ）
①x2=0 ②ax2+bx+c=0 ③
x2－3=
x ④a2+a－x=0 ⑤(m－1)x2+4x+
=0 ⑥
+
=
⑦
=2 ⑧(x+1)2=x2－9
A.2个 B.3个 C.4个 D.5个
2.方程2x(x－3)=-5(x－3)的解是（ ）
A.x=3 B.x=-
，x=3
C.x1=3，x2= D.x=－3
3.已知方程ax2+c=0(a≠0)有实数根，则a与c的关系是
A.c=0 B.c=0或a、c异号 C.c=0或a、c同号 D.c是a的整数倍
4.若2，3是方程x2+px+q=0的两实根，则x2+px+q可以分解为（ ）
A.(x－2)(x－3) B.(x+1)(x－6) C.(x+1)(x+5) D.(x+2)(x+3)
5.某厂改进工艺降低了某种产品的成本，两个月内从每件产品250元，降低到了每件160元，平均每月降低率为（ ）
A.15% B.20% C.5% D.25%
6．若
是一元二次方程
的两个根，则
的值（ ）
A 
B 
C 
D 
7.下列方程适合用因式分解解法解的是（ ）
A.x2－3x+2=0 B.2x2=x+4
C.(x－1)(x+2)=7 D.x2－11x+10=0
8.已知x=1是一元二次方程(m2－1)x2－mx+m2=0的一个根，那么m的值是（ ）
A.
或－1 B.－或 1 C.或 1 D.
9．三角形两边的长分别是8和6，第3边的长是一元二次方程
一个实数根，则该三角形的面积是
（ ）
A． 24 B. 24或
C.48
D.48或
10.下列两个三角形中，一定全等的是（ ）
A.有一个角是40°，腰相等的两个等腰三角形
B.两个等边三角形
C.有一个角是100°，底相等的两个等腰三角形
D.有一条边相等，有一个内角相等的两个等腰三角形
二、填空题（每题3分，共5题）
11.方程5(x2－x+1)=－3x+2的一般形式是__________，其二次项是__________，一次项是__________，常数项是__________.
12.关于x的方程mx2 -2x2+(m+4)x+2m+3=0，当m__________时，是一元二次方程，当m__________时，是一元一次方程.
13．
是方程
的一个根，则
=_______，另一个根是_______；
14．请你给出一个c值, c= ，使方程x2-3x+c=0无解。
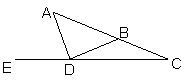15．如图：已知AD=DB=BC，∠C=250，则∠ADE=＿＿＿＿＿度.
三、按要求解下列方程（每题5分，共2题）
16．用配方法解下列方程 
（第15题图）
17．用适当的方法解下列方程 3x2+8x―3=0
四、解答题：（18-21每小题7分，22题8分，23题9分）
18. 桌子的桌面长为6米，宽为4米，台布面积是桌面面积的2倍，如果将台布铺在桌子上，各边垂下的长度相同，求这块台布的长和宽。
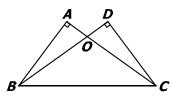
19．已知：如图，∠A=∠D=90°，AC=BD.求证：OB=OC；
 |
20. 小军同学家开了一个商店，今年1月份的利润是1000元，3月份的利润是1210元，请你帮助小军同学算一算，他家的这个商店这两个月的利润平均月增长率是多少？
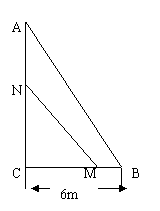21.如图，在直角ΔABC中，∠C=90o ，BC= 6
, AB=10. 点M从B点以1/s的速度向点C匀速移动，同时点N从C点以2/s的速度向点A匀速移动，问几秒钟后，ΔMNC的面积是ΔABC面积的？
 |
22 .（8分）. 西瓜经营户以2元／千克的价格购进一批小型西瓜，以3元／千克的价格出售，每天可售出200千克，为了促销，该经营户决定降价销售，经调查发现，这种小型西瓜每降价0．1元，每天可多售出40千克，另外，每天的房租等固定成本共花24元．该经营户要想每天盈利200元，应将每千克小型西瓜的售价降多少元?
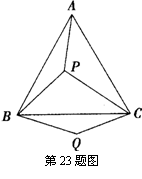
23、（9分）如图，P是等边三角形ABC内的一点，连结PA，PB，PC，以BP为边作∠PBQ=60°，且BQ=BP，连结CQ．
(1)观察并猜想AP与CQ之间的大小关系，并证明你的结论；
(2)若PA：PB：PC=3：4：5，连结PQ，试判断△PQC的形状，并说明理由．
 |
题目做完了，请你再细心检查一遍。