第二十四章<<圆>>单元测试
一.填空题(每题3分共36分)
1.如果圆的内接正六边形的边长为6cm，则其外接圆的半径为
2．已知一条弧的长是3
厘米, 这条弧所在圆的半径是6 厘米,则这条弧所对的圆心角是 度。
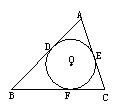
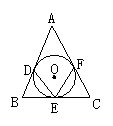
3．如图，△ABC三边与⊙O分别切于D，E，F，
已知AB=7cm，AC=5cm，AD=2cm，则BC=________．
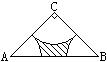
4．如图，在Rt△ABC中，∠C=90°，CA=CB=2。分别以
A、B、C为圆心，以
AC为半径画弧，三条弧与边AB
所围成的阴影部分的面积是______。
5．一个正多边形的中心角是36°，这个正多边形的边数是 .
6．一个圆锥的底面半径为3，高为4，则圆锥的侧面积是 。
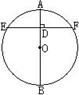
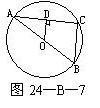
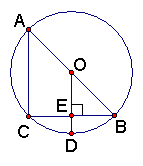
7.已知：如图，AB是⊙O的直径，弦EF⊥AB于点D，如果
EF=8，AD=2，则⊙O半径的长是 。
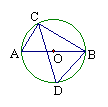8、如图，在⊙O中，AB为直径，∠ACB的平分线交⊙O于D，
则∠ABD= °
9.如图24—B—7，AB是⊙O的直径，OD⊥AC于点D， BC=6cm，则OD= cm.
10、如图，△ABC的三边分别切⊙O于D，E，F，若∠A=40°，则∠DEF= °
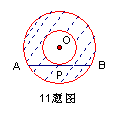
11.如图两个同心圆，大⊙O的弦AB切小⊙O于P，且AB=6，则阴影部分圆环的面积为 。
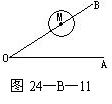
12.如图24—B—11，已知∠AOB=30°，M为OB边上一点，以M为圆心，2cm长为半径作⊙M，若点M在OB边上运动，则当OM= cm时，⊙M与OA相切。
|
二.选择题(每题3分共24分)
13.如图3，⊙Ｏ的半径为５，弦ＡＢ的长为８，Ｍ是弦ＡＢ上的动点，则线段ＯＭ长的最小值为（ ）
A．2 B．3 C．4 D．5
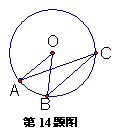
14．如图，点A、B、C在⊙O上，AO∥BC，∠OAC=20°，则∠AOB是( )
A. 1O° B. 20° C. 40° D. 70°
15．如图24—B—4，⊙O1和⊙O2内切，它们的半径分别为3和1，过O1作⊙O2的切线，切点为A，则O1A的长是（ ）
A．2
B．4 C．
D．
16．圆心在原点O，半径为5的⊙O,点P（-3，4）与⊙O的位置关系是（ ）.
A. 在⊙O内 B. 在⊙O上 C. 在⊙O外 D. 不能确定
17．两圆的半径分别为R＝5，r＝3，圆心距d＝6，则这两圆的位置关系是 ( ).
A．外离 B．外切 C．相交 D．内含
18．△ABC中，∠C＝90°，AC＝12cm，BC＝5 cm，若以C为圆心，5cm为半径作圆，则斜边AB与⊙O的位置关系是 ( ).
A．相离 B．相切 C．相交 D．不能确定
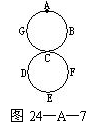19．如图24—A—7，两个半径都是4cm的圆外切于点C，一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行，蚂蚁在这8段路径上不断爬行，直到行走2006πcm后才停下来，则蚂蚁停的那一个点为（ ）
A．D点 B．E点 C．F点
D．G点
20. 如图，在△ABC中，已知∠C=90°，BC=3，AC=4，
则它的内切圆半径是（ ）
A．
B．
C．2 D．1
三.解答题
21．（本题8分）如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交
于D。
（1）请写出四个不同类型的正确结论；
① ；② ；
③
；④
。
（2）若BC=8，ED=2，求⊙O的半径。
22.（本题4分)已知在△ABC中，∠ A=90°，请用圆规和直尺作⊙P，使圆心P在AC上，且与AB、BC两边都相切。（要求保留作图痕迹，不必写出作法）
三、解答题．
23.
（5分）如图所示,已知两同心圆中,大圆的弦AB、AC切小圆于D、E,△ABC 的周长为12cm,求△ADE的周长.
|
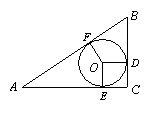
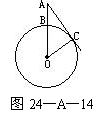24．（5分）如图24—A—14，已知⊙O的半径为8cm，点A为半径OB的延长线上一点，射线AC切⊙O于点C，BC的长为
，求线段AB的长。
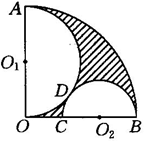25．（5分）如图，已知扇形AOB的半径为12，OA⊥OB，C为OB上一点，以OA为直线的半圆O与以BC为直径的半圆O相切于点D．求图中阴影部分面积．
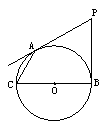26．（6分）如图，从点P向⊙O引两条切线PA，PB，切点为A，B，AC为弦，BC为⊙O的直径，若∠P=60°，PB=2cm，求AC的长．
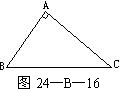
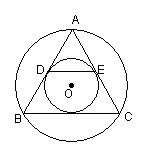
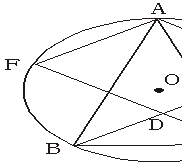27.(7分)如图16，⊙O上三点A、B、C，AB=AC，∠ABC的平分线交⊙O于点E，∠ACB的平分线交⊙O于点F，BE和CF相交于点D，四边形AFDE是菱形吗？验证你的结论.