九年级复习数学月考试题
一、选择题：（12×3分=36分）
1．在下列的计算中，正确的是( )
A.2x+3y=5xy B.（a+2）（a-2）=a2+4 C.a2•ab=a3b D.（x-3）2=x2+6x+9
 |
2．如图是一个物体的三视图，则该物体的形状是( )
A.圆锥 B.圆柱
|
3．如果-4是一元二次方程x2=c的一个根，则方程的另一个根为（ ）
A．16 B．4 C．-4 D．-16
4．Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以点C为圆心，2.5cm为半径作⊙C。则线段AB的中点D与⊙C的位置关系是（ ）
A．D在⊙C上 B．D在⊙C外 C．D在⊙C内 D．不能判断
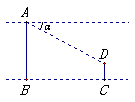
5．如图，两建筑物的水平距离BC为30米，从A点测得D
点的俯角α为30°，则建筑物AB比建筑物CD大约高（ ）
（结果保留两位小数，sin30°=0.5，cos30°=0.866，tan30°=0.577）
A．15米 B．34.65米 C．51.96米 D．17.31米
6．图中几何体（上半部为正三棱柱，下半部为圆柱）的主视图为（ ）
 |
A． B． C． D．
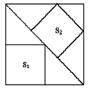
7．如图，大正方形中有2个小正方形，如果它们的面积分别是
S1、S2 ，那么S1、S2的大小关系是 ( )
(A) S1 > S2 (B) S1 = S2
(C) S1<S2 (D) S1、S2 的大小关系不确定
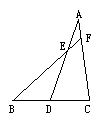8．如图，BD＝CD，AE：DE＝1：2，延长BE交AC于F，且AF＝4cm，则AC的长为（ ）
A、24cm B、20cm C、12cm D、8cm
9.（07泰安市）计算
的结果为（ ）
A．
B．
C．
D．
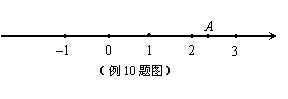10.（07漳州一中）如图，点
在数轴上表示的实数为
，则
等于（ ）
A.
B.
C.
D.
11.（07北京市）若
，则
的值为（ ）
A．
B．
C．0 D．4
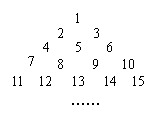
12.（07呼和浩特市）观察 右列三角形数阵：
则第50行的最后一个数是（ ）
Ａ．1225 Ｂ．1260 Ｃ．1270 Ｄ．1275
二、填空题：（6×3分=18分）
13、方程x2-2bx+3=0的一个解是-1,则b=___________.
14、方程x（x＋3）＝x＋3的解是
15、若x―
=2008 , 
,则
；
16 、若三角形的三边长分别为整数，周长为13，且一边长为4，则这三角形的最大边长是 ( ）
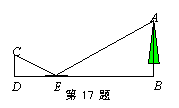
17．为测量校园平地上一棵大树的高度，学校数学兴趣小组做了如下的探索.他们根据光的反射原理，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面镜子放在离树底B有9米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=0.9米，若观察者目高CD=1.65米，则树的高度AB约为________米.
三、解答题：
18.
（07北京）(5分)计算：
19 (5分)(07兰州) 若
，则求
的值.
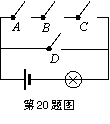
20．(6分)如图，电路图上有A、B、C、D四个开关和一个小灯泡，闭合开关D或同时闭合开关A、B、C都可使小灯泡发光．
（1）任意闭合其中一个开关，则小灯泡发光的概率等于 ；
（2）任意闭合其中两个开关，请用画树状图或列表的方法求出小灯泡发光的概率.
 |
21．(7分)如图，是学校背后山坡上一棵原航空标志的古柏树AB的示意图，在一个晴天里，数学教师带领学生进行测量树高的活动．通过分组活动，得到以下数据：
一是测得太阳光线AC与垂线AB的夹角∠CAB为150；
二是测得树在斜坡上影子BC的长为10m；
三是测得影子BC与水平线的夹角∠BCD为300；
请你帮助计算出树的高度AB （精确到0.1m）.
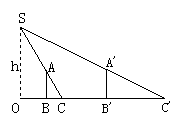
22．(8分)为了测量路灯（OS）的高度,把一根长1.5米的竹竿（AB）竖直立在水平地面上,测得竹竿的影子（BC）长为1米,然后拿竹竿向远离路灯方向走了4米（BB‘）,再把竹竿竖立在地面上, 测得竹竿的影长（B‘C‘）为1.8米,求路灯离地面的高度.
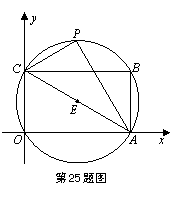
23 (4+4分)如图，已知矩形ABCO在坐标系的第一象限，它的长AO是宽OC的倍，且有两边在坐标轴上.将△ACO沿对角线AC翻折得△ACP，P点落在经过矩形ABCO四个顶点的⊙E上，⊙E的半径为R.
（1）用R的式子表示点B的坐标；
（2）若抛物线y=ax2+x+c经过P、A两点，请你判断点C是否在此抛物线上；
 | |||
 | |||
24．（ 6+2+2=10分） 已知二次函数
。
（1）结合函数
；
（2）根据（1）的结论，确定函数
的解析式；
（3）若一次函数
的图象交于三个不同的点，试确定实数
应满足的条件。
25、附加题(宁夏中考压轴题)（20分）已知直线
（其中k为常数），当k为任何实数时，直线都会经过定点A。抛物线
经过点A。
（1）求抛物线的解析式；
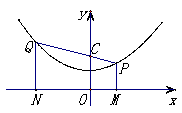
（2）如图，过C（0，2）任作一条直线，交抛物线于
P、Q两点，P、Q两点在x轴上的正投影分别为点
M、N，请探究PQ、PM和QN这三条线段之间的数量关系式；
（3）在第（2）问的条件下，在①MN2=2PM·QN,②MN2=4PM·QN两个等式中有一个成立，请判断哪一个成立，并证明这个成立的结论。