初三数学第一次调研考试试卷
一、填空题（每题3分计30分）
1．当
__________时，
无意义；
2．当k= 时，方程
是关于x的一元二次方程。
3．一个射箭运动员连续射靶5次，所得环数分别是8，6，10，7，9，则这个运动员所得环数的极差为 方差为 。
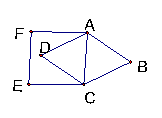
4．如图1，等腰三角形ABC的底边BC的长为a，以腰AB为直径的⊙O交BC于点D，则BD的长为 。
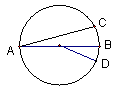
5．如图2，AB为⊙O的直径， 
，∠A=25°，则
∠BOD= 。
图（1） 图（2） 图（3）
6．如图3，菱形ABCD中，∠B=60°，AB=4，则以AC为边长的正方形ACEF的周长为
7．在半径为2的⊙O中，弦AB的长为
，则弦AB所对的圆心角∠AOB的度数是 。
8．⊙O的半径为5cm，P是⊙O内任一点，OP=3，则经过P点的最长弦为 cm，最短弦为 cm。
9．观察下列各式：
…
将你猜想到的规律用一个式子来表示： 。
10．如果圆的弦长等于半径，则这条弦所对的圆周角是 。
二、选择题（请将每题的答案填在表格内。每题3分计30分）
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
11．要比较两位同学在五次数学测验中谁的成绩比较稳定，应选用的统计量是
（A）平均数 （B）中位数 （C）众数 （D）方差
12．下列计算中，正确的是
A、
B、
C、
D、
13．下面是李刚同学在一次测验中解答的填空题，其中答对的是
A、若x2=4，则x＝2
B、方程x(2x－1)＝2x－1的解为x＝1
C、若x2+2x+k=0的一个根为1，则
D、若分式
的值为零，则x＝1，2
14．下列语句：①直径是弦；②弧是半圆；③长度相等的弧是等弧；④经过圆内一定点可以作无数条直径。其中错误的个数是
（A）1 （B）2 （C）3 （D）4
15．下列命题中，正确的是
（A）圆是轴对称图形，对称轴是圆的每一条直径；
（B）在同圆中，互相垂直的两弦不能互相平分；
（C）经过圆心的直线平分弦；
（D）垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。
16．
（A）0 （B）±2（C）±5（D）±
17．已知AB、CD是⊙O两条直径，则四边形ABCD为
A 平行四边形； B 菱形； C 矩形； D 正方形。
18．已知⊙O的半径为5㎝，弦AB∥CD，AB=6㎝，CD=8㎝，则AB与CD之间的距离为
（A）1㎝ （B）3㎝ （C）7㎝ （D）1㎝或7㎝
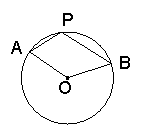
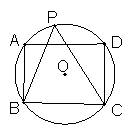
19．如图4，正方形ABCD内接于⊙O，P是
上任意一点，则
∠ABP+∠DCP等于
（A）90° （B）60° （C）45° （D）30°
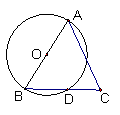
20．如图5，点P为⊙O的弧AB上任意一点，∠AOB=120°，则
∠P的度数是
（A）120° （B）60° （C）100° （D）不能确定
图（4） 图（5）
三、解答题
21、（6分）计算：
22、解方程（每题6分，计12分）
（1）
（2）
23．
（8分）
24．已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，
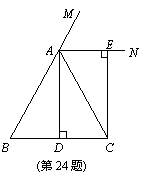（1）求证：四边形ADCE为矩形；
（2）当△ABC满足什么条件时，四边形
ADCE是一个正方形？并给出证明．（10分）
25．某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利45元，为了扩大销售、增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出4件，若商场平均每天盈利2100元，每件衬衫应降价多少元。（8分）
26．如图，△ABC的顶点都在⊙O上，AD是△ABC的高，AE是⊙O的直径。
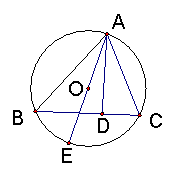求证：
（10分）
27．在直径为650㎜的排污管道中，污水面的宽度为600㎜，求污水的最大深度。（10分）
28．在△ABC中，AB=AC，CG⊥BA交BA的延长线于点G．一等腰直角三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．
（1）在图15-1中请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；
（2）当三角尺沿AC方向平移到图2所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE＋DF与CG之间满足的数量关系，然后证明你的猜想；
（3）当三角尺在（2）的基础上沿AC方向继续平移到图3所示的位置（点F在线段AC上，且点F与点C不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）（13分）
．
29．(本题13分)如图1，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F．
(1)求证：EF+
AC＝AB；
(2)点C1从点C出发，沿着线段CB向点B运动(不与点B重合)，同时点A1从点A出发，沿着BA的延长线运动，点C1与点A1的运动速度相同，当动点C1停止运动时，另一动点A1也随之停止运动．如图2，A1F1平分∠BA1C1，交BD于点F1，过点F1作F1E1⊥A1C1，垂足为E1，请猜想F1E1、A1C1与AB三者之间的数量关系，并证明你的猜想；
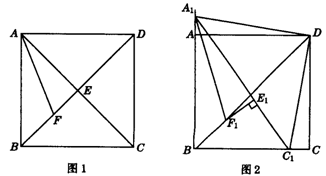(3)在(2)的条件下，当A1E1=3，C1E1＝2时，求BD的长