初三数学上学期八校联考
姓名_______-_得分_________-
一、选择题(每小题2分,共24分)
1.下列图案中是轴对称图形的是( )
2.已知等腰三角形的一个底角等于30°,则这个等腰三角形的顶角等于
A、150° B、120° C、75° D、30°
3.在同一平面内,用两个边长为a的等边三角形纸片(纸片不能裁剪)可以拼成的四边形是
A.矩形 B.菱形 C.正方形 D.梯形
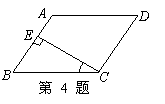 4.如图,在平面四边形
4.如图,在平面四边形![]() 中,
中,![]() ,
,![]() 为垂足.如果
为垂足.如果![]() ,则
,则![]() ( )
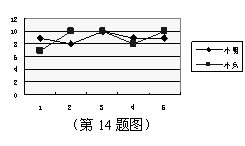
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列各式中正确的是( )
A.![]() B.
B.![]()
C.![]() D.
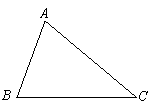
D.![]()
6.小明同学将某班级毕业升学体育测试成绩(满分30分)统计整理,得到下表,则下列说法错误的是( )
| 分数 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 人数 | 2 | 4 | 3 | 8 | 10 | 9 | 6 | 3 | 1 |
 A.该组数据的众数是24分 B.该组数据的平均数是25分
A.该组数据的众数是24分 B.该组数据的平均数是25分
C.该组数据的中位数是24分 D.该组数据的极差是8分
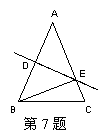
7、顺次连结等腰梯形四边中点得到一个四边形,再顺次连结所得四边形四边中点得到的图形是( )
A、等腰梯形 B、直角梯形 C、菱形D、矩形
8、如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于
点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( ).
 A.12cm B.10cm C. 8cm
D. 6cm
A.12cm B.10cm C. 8cm
D. 6cm
9.如图,已知等腰梯形![]() 中,
中,![]() ,
,![]() ,
,
![]() ,则此等腰梯形的周长为( )
,则此等腰梯形的周长为( )
A.19 B.20
C.21 D.22
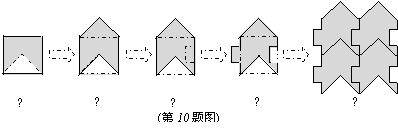
10.如图,把边长为2的正方形的局部进行图①~图④的变换,换成图⑤,则图⑤的面积是( )。
A、18 B、16 C、12 D、8
 | |||
 | |||
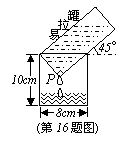
11.如图,在把易拉罐中水倒入一个圆水杯的过程中,若水杯中的水在点P与易拉罐刚好接触,则此时水杯中的水深为( )。
A、2cm B、4cm C、6cm D、8cm
 12.如图,边长为1的正方形
12.如图,边长为1的正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到正方形
到正方形![]() ,图中阴影部分的面积为( )
,图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题3分,共12分)
13、![]() ;
;![]() 有意义的条件是 .
有意义的条件是 .
14、小明和小兵两人参加学校组织的理化实验操作测试,近期的5次测试成绩如上图所示,则小明5次成绩的极差R1与小兵5次成绩的极差R2之间的大小关系为R1 R2 .(填“>”、“<”、“=”)
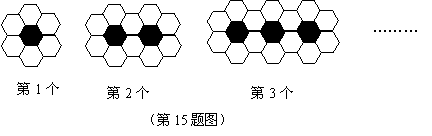 |
 15.用黑白两种颜色的正六边形地板砖按图所示的规律,拼成若干地板图案,则第
15.用黑白两种颜色的正六边形地板砖按图所示的规律,拼成若干地板图案,则第![]() 个图案中白色的地板砖有__________块.
个图案中白色的地板砖有__________块.
16.如图(5),把矩形纸条![]() 沿
沿![]() 同时折叠,
同时折叠,
![]() 两点恰好落在
两点恰好落在![]() 边的
边的![]() 点处,若
点处,若![]() ,
,
![]() ,
,![]() ,则矩形
,则矩形![]() 的边
的边![]() 长为________。
长为________。
三、解答题(每小题6分,共24分)
17.计算:![]()
18.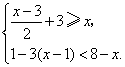
19.如图,菱形公园内有四个景点,请你用两种不同的方法,按下列要求设计成四个部分:⑴用直线分割;⑵每个部分内各有一个景点;⑶各部分的面积相等。(可用铅笔画,只要求画图正确,不写画法)
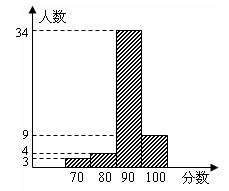 20.如图是某中学在一次社会百科知识竞赛活动中,抽取的一部分同学的测试成绩为样本,绘制的成绩统计图.请根据该统计图,解答下面问题:
20.如图是某中学在一次社会百科知识竞赛活动中,抽取的一部分同学的测试成绩为样本,绘制的成绩统计图.请根据该统计图,解答下面问题:
(1)本次测试中,抽样的学生有 人;
(2)这次测试成绩的众数为 ;
(3)若这次测试成绩90分以上(含90分)
为优秀,则优秀率为 .
四、解答题(每小题7分,共28分)
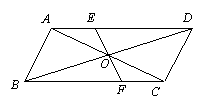 21.如图,平行四边形ABCD的对角线交于点O,过点O的直线交AD于E、交BC于F,
21.如图,平行四边形ABCD的对角线交于点O,过点O的直线交AD于E、交BC于F,
求证:(1)△AOE≌△COF;
(2)四边形AECF是平行四边形.
22. 某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1) 写出所有选购方案(利用列表的方法或树状图表示);
(2) 如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
23.如图,在![]() 中,CB=AC,
中,CB=AC, ![]() .
.
(1)作AC的垂直平分线交BC于点D,连接AD。(要求:用尺规作图,不写作法,保留作图痕迹)
(2)求 BAD的度数。
(3)若AB=8cm,△ABD的周长等于18cm,求AC的长。
 |
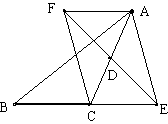
24、已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF。
(1) 求证:AF=CE;
(2) 若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论。
五、(本题8分)
25.如图10(单位:m),等腰三角形ABC以2米/秒的速度沿直线L向正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y![]() 。
。
(1)写出y与x的关系式;(3分)
(2)当x=2,3.5时,y分别是多少?(2分)
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?(3分)
 |
26.(本题满分8分)
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
⑴ 请在网格中建立平面直角坐标系, 使A点坐标为(-2,4),B点坐标为(-4,2);
⑵ 在第二象限内的格点上画一点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是 , △ABC的周长是 (结果保留根号);
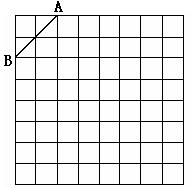 ⑶ 画出△ABC以点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.
⑶ 画出△ABC以点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.
27.请阅读下列材料:(本题6分)
问题:现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形。要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。
小东同学的做法是:设新正方形的边长为x(x>0)。依题意,割补前后图形的面积相等,有x2=5,解得x=![]() 。由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长。于是,画出如图②所示的分割线,拼出如图③所示的新正方形。
。由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长。于是,画出如图②所示的分割线,拼出如图③所示的新正方形。
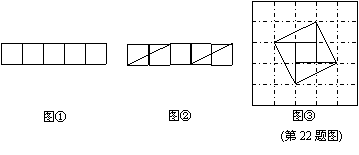 |  | ||
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的正方形,排列形式如图④,请把它们分割后拼接成一个新的正方形。要求:在图④中画出分割线,并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。
 28.(本题10分)
28.(本题10分)
在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直上,另一条直角边恰好经过点B.
(1)在图15-1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)