新人教九年级数学上第二次月考试题
班级 姓名 学号 成绩
一、选择题(每小题3分,共33分)
1、在式子![]() 中,是最简二次根式的式子有(
)个
中,是最简二次根式的式子有(
)个
A、2 B、3 C、1 D、0
2、在平面直角坐标系中,点P(-2,3)关于原点对称的点在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
3、已知a、b、c是ΔABC三边长且方程![]() 有两相等的实数根,则这个三角形是( )
有两相等的实数根,则这个三角形是( )
A、等腰三角形 B、等边三角形 C、不等边三角形 D、直角三角形
 4、在半径等于5cm的圆内有长为
4、在半径等于5cm的圆内有长为![]() cm的弦,则此弦所对的圆周角为( )
cm的弦,则此弦所对的圆周角为( )
A、60º或120º B. 30º或120º C. 60º D. 120º
5、如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,
则线段OM长的最小值为( )
A、2 B、3 C、4 D、5
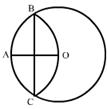 6、AB是⊙O的弦,ÐAOB =80°,则AB所对的圆周角是( )
6、AB是⊙O的弦,ÐAOB =80°,则AB所对的圆周角是( )
A.40° B.40° 或140° C.20° D.80°或100°
7.如图, ⊙O的半径OA=6, 以A为圆心,OA为半径的弧交⊙O
于B、C两点, 则BC= ( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
8.如图,![]() 内接于⊙O,
内接于⊙O,![]() ,
,![]() ,则⊙O的半径为(
)
,则⊙O的半径为(
)
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.按下列程序计算,最后输出的答案是( )
![]()
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
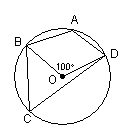
10.如图,四边形ABCD内接于⊙O,若∠BOD=![]() ,
,
则∠DAB的度数为( )
A.![]() B.
B.![]() C.
C.![]() ; D.
; D.![]()
11.如图是每个面上都标有一个汉字的正方体的平面展开图,
在此正方体上与“水”字相对的面上的汉字是( )
 A.“秀” B.“丽” C.“江” D.“城”
A.“秀” B.“丽” C.“江” D.“城”
二、填空题(每小题3分,共21分)
1. 若圆的半径为2cm,圆中一条弦长为2![]() cm,则此弦中点到此弦
cm,则此弦中点到此弦
所对劣弧的中点的距离为________.
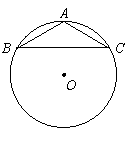
2、 如图A、B、C是⊙O上的三点,∠BAC=30°,则∠BOC的大小是 °

 3、如图,⊙O的半径为5cm,圆心到弦AB的距离为3cm,则弦AB的长为________cm;
3、如图,⊙O的半径为5cm,圆心到弦AB的距离为3cm,则弦AB的长为________cm;
4、在直径为![]() 的圆柱形油槽内装入一些油后,截面如图所示,如果油面宽
的圆柱形油槽内装入一些油后,截面如图所示,如果油面宽![]() ,那么油的最大深度是_______
,那么油的最大深度是_______![]() .
.
5、如图,在⊙O 中,弦![]() ,圆周角
,圆周角![]() ,则⊙O的直径等于________
,则⊙O的直径等于________![]() .
.
 |
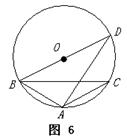
6、如图,AB为半圆O的直径,C、D是 上的三等分点,
若 ⊙O的半径为1,E为线段AB上任意一点,计算图中
阴影部分的面积为________.
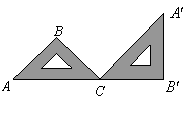
7.如图,一块等腰直角的三角板![]() ,在水平桌面上绕点
,在水平桌面上绕点![]() 按顺时针方向旋转到
按顺时针方向旋转到![]() 的位置,使
的位置,使![]() 三点共线,那么旋转角度的大小为
三点共线,那么旋转角度的大小为
三、解答题(每小题6分,共18分)
1、如图,⊙O是![]() 的外接圆,且
的外接圆,且![]() ,求⊙O的半径.
,求⊙O的半径.
 |
 2、如图,已知⊙O的半径为2,弦AB的长为2
2、如图,已知⊙O的半径为2,弦AB的长为2![]() ,点C与点D分别是劣弧
,点C与点D分别是劣弧![]() 与优弧
与优弧![]() 上的任一点(点C、D均不与A、B重合).
上的任一点(点C、D均不与A、B重合).
(1)求∠ACB;(2)求△ABD的最大面积.
3、某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的平均月增长率.
四、解答题(每小题7分,共21分)
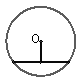
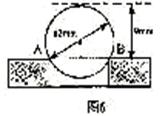
1、工程上常用钢珠来测量零件上小孔的直径.假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图6所示,求这个小孔的直径AB是多少毫米?
 |
2、“便民”水泥代销点销售某种水泥,每吨进价为250元.如果每吨销售价定为290元时,平均每天可售出16吨.
(1)若代销点采取降低促销的方式,试建立每吨的销售利润![]() (元)与每吨降低
(元)与每吨降低![]() (元)之间的函数关系式.
(元)之间的函数关系式.
(2)若每吨售价每降低5元,则平均每天能多售出4吨.问:每吨水泥的实际售价定为多少元时,每天的销售利润平均可达720元.
3、商场购进一批单价为16元的日用品,销售一段时间后,为了获得更多的利润,商场决定提高销售价格,经调查发现,如果按每件20元的价格销售时,每月能卖360件,若按每月25元的价格销售时,每月能卖210件.若每月销售件数y(件)与价格x(元/件)满足关系式:y=Kx+b.(1)求K与b的值.(2)为了获得最大利润,商品价格应定为每件多少元?
最大利润是多少元?
五、(每小题9分,共27分)
1、已知实数a、b分别满足![]() .求
.求![]() 的值.
的值.
2、如图⊙O半径为2,弦BD=![]() ,A为弧BD的中点,E为弦AC的中点,且在BD上.
,A为弧BD的中点,E为弦AC的中点,且在BD上.
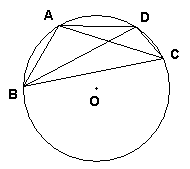 求:四边形ABCD的面积.
求:四边形ABCD的面积.
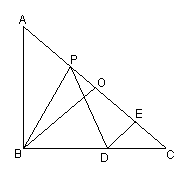 3、如图,在等要直角三角形ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,
3、如图,在等要直角三角形ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,![]() ,垂足为点E.
,垂足为点E.
⑴求证:PE=BO
⑵设AC=2a,AP=x,四边形PBDE的面积为y,
求y与x之间的函数关系式,并写出自变量的取值范围.
新人教九年级数学上第二次月考试题
参考答案
一、1、B 2、D 3、A 4、A 5、B 6、B 7、A 8、B 9、C 10、D 11、B
二、1、1cm 2、60 3、8 4、2 5、3.6 6、![]() π 7、135°
π 7、135°
三、1、连接OA,OB,⊙O的半径是16.9
2、120°,![]()
3、20%
四、1、![]() 2、y=(290-x)-250=40-x ,定价 280元
2、y=(290-x)-250=40-x ,定价 280元
3、k=-30,b=960, 定价 24元,1920元
五、
1、根据题意,a,b是方程![]()
![]() 的实数根
的实数根
⑴当![]() 时,a+b=-2,ab=2,
时,a+b=-2,ab=2,![]()
![]()
⑵![]() 的实数根是
的实数根是![]()
![]()
当![]() =-1+
=-1+![]() 时,
时,![]()
![]()
当![]() =-1-
=-1-![]() 时,
时,![]()
![]()
2、![]()
3、⑴∵△ABC为等腰直角三角形,O 为斜边 AC 的中点,
∴BO⊥AC,BO=CO=AC ∠C=OBC=45°,DE⊥AC,BO⊥AC,BO![]() DE,
DE,
∵PB=PD
∴∠PBD=∠PDB, ∠POB=∠PED=90°,
∠PBO=∠PBD-∠OBC=∠PDB=∠OBC=∠PDB-∠C=∠DPE
∴△PBO≌△DPE,
∴PE=BO
⑵∵AC=2a,AP=x,
∴AO=BO=PE=a,DE=PO=EC=a-x,EO=x,
∴y= S![]() + S
+ S![]() =
=![]()
![]() ,
,
x取值范围0<x<a