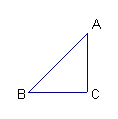第五次月考
一 选择题（共10小题，每小题３分，计30分）
1. 如图，在⊿ABC中，AC=3，BC=4，AB=5，则tanB的值是（ ）
A. 
B. 
C. 
D.
2. △ABC中，∠A、∠B都是锐角，且sinA=
，cosB=
，则△ABC的形状是(
)
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
3. .在△ABC中，AB=AC=4，BC=2，则4cosB等于( )
A.1 B.2
C.
D.
4. 如果∠A为锐角，且cosA=
，那么∠A的范围是
A . 0°<∠A≤30° B.30°<∠A<45°
C. 45°<∠A<60° D.60°<∠A<90°
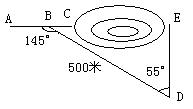
5 如图，沿AC方向开山修路，为了加快施工进度，要在小山的另一边同时施工。从AC上的一点B，取∠ABD=145°，BD=500米，∠D=55°，要使A、C、E成一直线，那么开挖点E离点D的距离是（ ）
A. 500sin55°米 B. 500cos55°米
C. 500tan55°米 D. 500tan35°米
6. 下列各关系式中，属于二次函数的是(x为自变量) （ ）
A.y=
x2 B.y=
C.y=
D.y=a2x
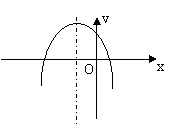7. 已知二次函数
的图象如右图所示，
则ａ、ｂ、ｃ满足（ ）
Ａ. a＜0，b＜0，c＞0 B. a＜0，b＜0， c＜0
C. a＜0，b＞0，c＞0 D. a＞0，b＜0， c＞0
8. 下列说法错误的是 ( )
A.二次函数y=3x2中，当x>0时，y随x的增大而增大
B.二次函数y=－6x2中，当x=0时，y有最大值0
C.a越大图象开口越小，a越小图象开口越大
D.不论a是正数还是负数，抛物线y=ax2(a≠0)的顶点一定是坐标原点
9. 在同一坐标系中，作y=x2，y=－x2，y=
x2的图象，它们的共同特点是( )
A.抛物线的开口方向向上
B.都是关于x轴对称的抛物线，且y随x的增大而增大
C.都是关于y轴对称的抛物线，且y随x的增大而减小
D.都是关于y轴对称的抛物线，有公共的顶点
10. 已知a<－1，点(a－1，y1)，(a，y2)(a+1，y3)都在函数y=x2的图象上，则( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
二
填空题（共6小题，每小题３分，计18分）
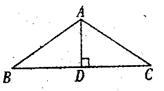
11. 如图，等腰三角形ABC的顶角为1200，
腰长为10，则底边上的高AD=
12. 某段公路每前进100 m，就升高4 m，则路面的坡度约为_____
13. 如果由点A测得点B在北偏西20°的方向，那么由点B测得点A的方向是______
14. 若函数y=(k2－4)x2+(k+2)x+3是二次函数，则k______
15. 写出一个开口向上，顶点是y轴上的二次函数的表达式：
16. 在边长为6 cm的正方形中间剪去一个边长为x cm(x<6)的小正方形，剩下的四方框形的面积为y，y与x之间的函数关系是______
三 解答题（共8小题，计52分，解答应写出过程）
17（本题满分6分）求值：sin245°- cos60°+ tan60°·cos230°
18.（本题满分10分）如图，一位篮球运动员跳起投篮，球沿抛物线
运行，然后准确落入篮框内．已知篮框的中心离地面的距离为3.05米．
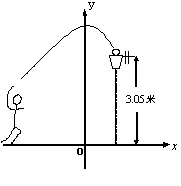（1）球在空中运行的最大高度为多少米？
（2）如果该运动员跳投时，球出手离地面的高度为2.25米，请问他距离篮框中心的水平距离是多少？
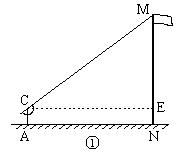19. （本小题满分12 分）在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下方案（如图①所示）：
（1）在测点A处安置测倾器，测得旗杆顶部 M 的仰角∠MCE =α；
（2）量出测点A到旗杆底部N的水平距离AN = m；
（3）量出测倾器的高度AC = h．
根据上述测量数据，即可求出旗杆的高度MN．
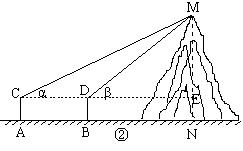
如果测量工具不变，请仿照上述过程，设计一个测量某小山高度（如图②）的方案：
（1）在图②中，画出你测量小山高度 MN 的示意图（标上适当字母）；
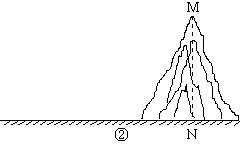（2）写出你设计的方案．
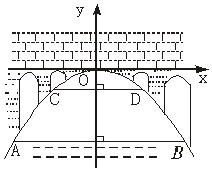
20. （本小题满分12 分）有一座抛物线形拱桥，桥下面在正常水位时AB宽20米，水位上升3米就达到警戒线CD，这时水面宽度为10米;
(1)在如图的坐标系中，求抛物线的表达式.
(2)若洪水到来时，再持续多少小时才能到拱桥顶？(水位以每小时0.2米的速度上升)
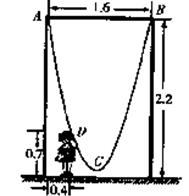
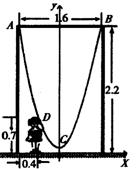
21（本小题满分12 分）如图，一单杠高2.2米，两立柱之间的距离为1.6米，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状．
（1）一身高0.7米的小孩站在离立柱0.4米处，其头部刚好触上绳子，求绳子最低点到地面的距离；
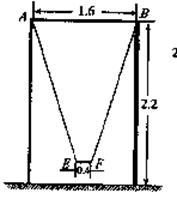
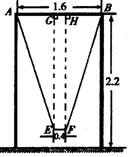
（2）为供孩子们打秋千，把绳子剪断后，中间系一块长为0.4米的木板，除掉系木板用去的绳子后，两边的绳长正好各为2米，木板与地面平行．求这时木板到地面的距离（供选用数据：
≈1.8，
≈1.9，
≈2.1．）
（1） （2）
参考答案：
一、1. A 2.B 3. A 4. D 5. B 6. A 7. A 8. C 9. D 10. C
二、11．5 12. 1∶24.98 13. 南偏东20° 14. ≠±2 15.
16. y=36－x2
三、17. 解：原式= 
（2分）
= 
（6分）
18.解：⑴ ∵抛物线 的顶点为（0，3.5）
∴最大高度为3.5米 (4分)
⑵ 在中 当
时 
∴
∴
又∵
＞0 ∴
…………………… (8分)
当
时 
∴
∴
又∵＜0 ∴
…………………… （11分）
故运动员距离篮框中心水平距离为 1.5+2.5 = 4 …………………… （12分）
19.解：（1）正确画出示意图． （4分）
（2）① 在测点A处安置测倾器，测得此时山顶M的仰角 ∠MCE = α；
② 在测点A与小山之间的B处安置测倾器（A、B与N在同一条直线上），测得此时山顶M的仰角 ∠MDE = β；
③ 量出测倾器的高度AC = BD = h ，以及测点A、B之间的距离AB = m ．
根据上述测量数据，即可求出小山的高度MN． （12分）
20.解：(1)设拱桥顶到警戒线的距离为m.
∵抛物线顶点在(0，0)上，对称轴为y轴,
∴设此抛物线的表达式为y=ax2(a≠0).
依题意：C(－5，－m)，A(－10，－m－3).
∴
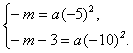
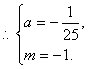
∴抛物线表达式为y=
8分 
(2)∵洪水到来时，水位以每小时0.2米的速度上升，m=1,
∴从警戒线开始再持续
=5(小时)到拱桥顶.
12分
（1） （2）
21解：（1）如图，建立直角坐标系， …………2分
设二次函数解析式为 y＝ax2＋c …………3分
∵ D（－0.4，0.7），B（0.8，2.2）， …………4分
∴ 
…………5分
∴ 
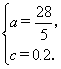
∴绳子最低点到地面的距离为0.2米． …………7分
（2）分别作EG⊥AB于G，FH⊥AB于H …………8分
AG＝
（AB－EF）
＝（1.6－0.4）＝0.6．
在Rt△AGE中，AE＝2，
EG＝
＝
＝≈1.9．
…………11分
∴ 2.2－1.9＝0.3（米）．
∴ 木板到地面的距离约为0.3米． …………12分