九年级数学综合复习题(一)
姓名 学号 得分
A卷(共100分)
一 选择题(每小题3分,本大题共24分)
1.已知一元二次方程![]() ,它的解是( )
,它的解是( )
(A)0 (B)2 (C)0,-2 (D)0,2
2.计算(-x)![]() •(-x)
•(-x)![]() 的正确结果是( ).
的正确结果是( ).
(A)x![]() (B)-x
(B)-x![]() (C)x
(C)x![]() (D)-x
(D)-x![]()
3.正方体的表面展开图不可能是( ).

4.在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
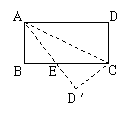 5.如图,将矩形纸片ABCD沿对角线AC对折,使点D落在点D′
5.如图,将矩形纸片ABCD沿对角线AC对折,使点D落在点D′
位置,AD′与BC交于点E,若该矩形纸片的周长是32cm,
则△ABE的周长是( ).
(A)8 (B)12 (C)16 (D)20
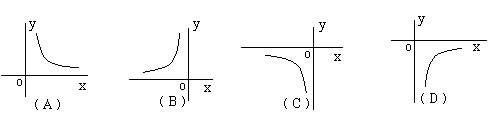 6、反比例函数y=-
6、反比例函数y=-![]() (x<0)的图象是( ).
(x<0)的图象是( ).
7. 下列各图中,不是中心对称图形的是( )

(A) (B) (C) (D)
8、下列关于二次函数y=-3(x+1)![]() +2图象的描述正确的有( )个.
+2图象的描述正确的有( )个.
① 开口向下 ② 顶点坐标为(1,2)
③ 与y轴的交点是(0,2) ④ 函数有最大值,且最大值为2
(A)1 (B)2 (C)3 (D)4
二 填空题(每小题3分,本大题共24分)
9.函数![]() 中,自变量
中,自变量![]() 的取值范围是
的取值范围是
10.根据国务院全面实行农村义务教育经费保障机制改革的精神,据《潇湘晨报》2月28日报道:2007年春季开学,我省投入19.8114亿元,对农村义务教育阶段的学生实行“两免一补”.19.8114亿元用科学记数法(保留两个有效数字)表示为___________元.
 |
11.方程-2x(x+1)=x+1的解是____________.
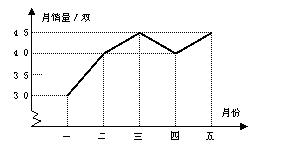
12.某鞋店老板将某种品牌的皮鞋5个月
的月销量绘成了折线统计图(如图所示),
则该鞋店这5个月这种皮鞋月销售量的
中位数为__________双.
13. 在![]() 中,
中,![]() ,
,![]() ,则
,则![]() .
.
14. 不等式组![]() 的最小整数解是
.
的最小整数解是
.
 15. 在ΔABC中,AB=AC=6cm,CD是AB边上的高,且CD=3cm,则∠A= .
15. 在ΔABC中,AB=AC=6cm,CD是AB边上的高,且CD=3cm,则∠A= .
16. 如图,△ABC是边长为6cm的等边三角形,被一平行
于BC的矩形所截,AB被截成三等分,则图中阴影部分的
面积为
| |
三 解答题(每小题6分,本大题共18分)
17.解答下列各题(每小题6分,本大题共18分)
(1)计算:+|-7|+()0+()-1-6tan30º. (2)解方程:![]()
(3)化简求值:
![]() •(1-
•(1-![]() )
)
其中实数x、y满足![]() +(2y+3)
+(2y+3)![]() =0
=0
四、(每小题8分,本大题共16分)
18. 如图,在梯形ABCD中,AD∥BC,AD=5cm,BC=8cm,M是CD的中点,P是BC边上的一动点(P与B,C不重合),连结PM并延长交AD的延长线于Q.
(1)试说明△PCM≌△QDM.
 (2)当P在B,C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.
(2)当P在B,C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.
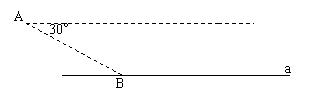
19. 一次战斗中,我武装直升飞机在空中A处侦察到敌方坦克在B处正沿直线a以每秒20米的速度逃跑,此时,我方直升飞机的高度为40米,测得敌坦克的俯角为30°.我直升飞机立即沿水平方向以每秒40米的速度追击,已知在飞机上测得敌坦克的俯角为60°时炮弹最易击中坦克,那么从A处起几秒钟后开火时机最好?(精确到0.1秒,参考数据:![]() ,
,![]() )
)
 |
五、(每小题9分,本大题共18分)
20. 如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于M、N两点.已知点N的坐标为(
的图象交于M、N两点.已知点N的坐标为(![]() ,
,![]() ),点M的横坐标为2.
),点M的横坐标为2.
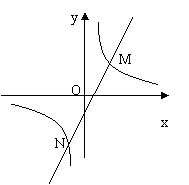 (1)求反比例函数和一次函数的解析式;
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使反比例函数的值大于一次函数的取值范围.
21.金坛箱包厂生产一种旅行包,每个旅行包的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次性订购量超过100个时,每多定一个,订购的全部旅行包的出厂单价就降低0.02元。根据市场调查,销售商一次性订购量不会超过550个。
⑴设销售商一次订购量为x个,旅行包的实际出厂单价为y元,写出当一次订购量超过100个时,y与x的函数关系式.
⑵求当销售商一次性订购量为多少个旅行包时,可使该厂获得利润6000元?(售出一个旅行包的利润=实际出厂单价-成本)
 B卷(共50分)
B卷(共50分)
一、填空题(每小题3分,本大题共15分)
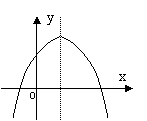
22.抛物线y=ax![]() +bx+c的图象如图所示,
+bx+c的图象如图所示,
则abc______0.(选填:>、<、=)
23.已知抛物线过点A(![]() ,0)和B(3,0)两点,与y轴的正半轴交于点C,且OC=
,0)和B(3,0)两点,与y轴的正半轴交于点C,且OC=![]() ,则这条抛物线的解析式是
。
,则这条抛物线的解析式是
。
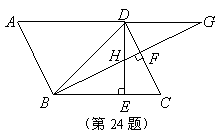 24.如图,已知
24.如图,已知![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 相交于
相交于![]() ,
,![]() 的延长线相交于
的延长线相交于![]() ,下面结论:
,下面结论:
①![]() ②
②![]()
③![]() ④
④![]()
其中正确的结论是
 25. 已知方程
25. 已知方程![]() 有一根大于0且小于1,则实数
有一根大于0且小于1,则实数![]() 的取值范围是
的取值范围是
26.方格纸中小正方形的边长为1,在直线a、b上按某规律取点A1、A2、A3、┉,B1、B2、B3、┉,分别记矩形A1C1B1O、A2C2B2O、A3C3B3O┉的面积为S1、S2、S3┉,
照此规律 S20=__________.
二、解答题(每小题7分,本大题共14分)
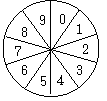 27.小明与小颖用如图所示的转盘玩填数游戏(转盘被10等分):转动转盘,当转盘停止后每人将指针指向的数字填在各自的方格内(规定小颖先填)转动三次后谁填出的数大谁获胜。第一次转出的是数5,两人已经填在了方格中.
27.小明与小颖用如图所示的转盘玩填数游戏(转盘被10等分):转动转盘,当转盘停止后每人将指针指向的数字填在各自的方格内(规定小颖先填)转动三次后谁填出的数大谁获胜。第一次转出的是数5,两人已经填在了方格中.
(1)若第二次转出的数是6,小颖应填在哪格?为什么?
(2)假设小颖将第二次转出的数6填在了左边一格,小明
应将6填在左边一格还是中间一格获胜的概率大些?为什么?
 |  | ||
28.下岗职工王阿姨利用自己的一技之长开办了“爱心服装厂”,计划生产甲、乙两种型号的服装共40套投放到市场销售.已知甲型服装每套成本34元,售价39元;乙型服装每套成本42元,售价50元.服装厂预计两种服装的成本不低于1536元,不高于1552元.
(1)问服装厂有哪几种生产方案?
(2)按照(1)中方案生产,服装全部售出至少可获得利润多少元?
(3)在(1)的条件下,服装厂又拿出6套服装捐赠给某社区低保户,其余34套全部售出,这样服装厂可获得利润27元.请直接写出服装厂这40套服装是按哪种方案生产的.
三.解答题(本大题10分)
29. 已知四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 绕
绕![]() 点旋转,它的两边分别交
点旋转,它的两边分别交![]() (或它们的延长线)于
(或它们的延长线)于![]() .
.
当![]() 绕
绕![]() 点旋转到
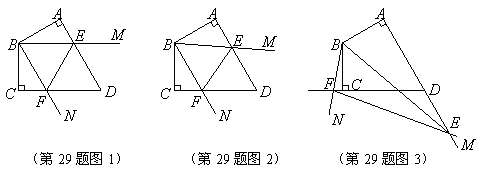
点旋转到![]() 时(如图1),易证
时(如图1),易证![]() .
.
当![]() 绕
绕![]() 点旋转到
点旋转到![]() 时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段
时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段![]() ,
,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
 |
五(本大题11分)
30.如图,在平面直角坐标系中,二次函数的顶点为C![]() ,且在x轴上截得的线段AB的长为6.
,且在x轴上截得的线段AB的长为6.
(1)求二次函数的解析式;
(2)在y轴上求作一点P(不写作法)使PA+PC最小,并求出点P的坐标;
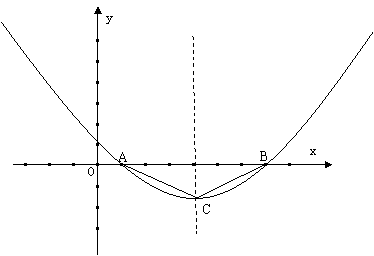 (3)在x轴上方的抛物线上,是否存在点Q,使得以Q、A、B三点为顶点的三角形与ΔABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.
(3)在x轴上方的抛物线上,是否存在点Q,使得以Q、A、B三点为顶点的三角形与ΔABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.