九年级下学期数学试卷
| 得分 | 评卷人 |
|
|
|
一、选择题（每小题3分，共30分）
1．下列方程中，关于x的一元二次方程的是 （ ）
A.
B.
C.
D.
2．下列根式是最简二次根式的是
( )
A.
B.
C.
D.
3．已知平面内两圆的半径分别为4和6，圆心距是2，则这两个圆的位置关系是（ ）
A.内切 B.相交 C.外切 D.外离
4．利用配方法解方程x2-12x+25=0可得到下列哪一个方程 （ ）
A.(x+6)2=11 B.(x-6)2=-11 C.(x-6)2=11 D.(x+6)2=51
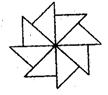5．右图可以看作是一个等腰直角三角形旋转若干次而生成的，
则每次旋转的度数可以是 （ ）
A.900 B.600 C.450 D.300
6．方程 (x -1)2= 1 的根是 （ ）
A.x =2 B.x = 0 C.x1= -2, x2=0 D.x1= 2, x2=0
7．已知圆锥的母线长为6cm，底面圆的半径为3cm，则此圆锥侧面展开图的面积为( )
A.18
cm2
B.36cm2
C.12cm2
D.9cm2
8．我国政府为解决老百姓看病难的问题，决定下调药品的价格，某种药品经过两次降价后，由每盒60元下调至52元，若设每次平均降价的百分率为x ，由题意可列方程为 （ ）
A.52+52x2=60 B.52(1+ x)2=60 C.60-60 x2=52 D.60(1- x)2=52
9．已知正六边形的周长为24cm，一圆与它各边都相切，则这个六边形的面积为（ ）
A.12
cm2
B.24 cm2
C.48 cm2
D.96 cm2
10．若将函数y=2x2的图象向右平行移动1个单位，再向上平移5个单位，可得到（ ）
A.y=2(x-1)2-5 B.y=2(x-1)2+5 C.y=2(x+1)2-5 D.y=2(x+1)2+5
| 得分 | 评卷人 |
|
|
|
二、填空题(每小题3分，共18分)
11．二次函数y＝3 (x +2)2 -1图象的顶点坐标是 .
12．已知点A(a,1)与点A´(5,b)是关于原点O的对称点,则a= ；b= .
13．袋中放有北京08年奥运会吉祥物五福娃纪念币一套，
依次取出（不放回）两枚纪念币，求取出的两枚纪念
币中恰好有一枚是“欢欢”的概率是 .
14．若
，则
.
15．如果关于x的一元二次方程mx2+2x－1=0有两个不相等的实数根，那么m的取值范围是
.
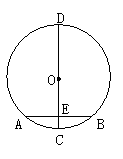
16. “圆材埋壁”是我国古代著名数学著作《九章算术》中的一个
问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，
锯道长一尺，问径几何？”此问题的实质就是解决下面的问题：
“如图，CD为⊙O的直径，弦AB⊥CD于点E，CE=1，AB=10，
求CD的长”。根据题意可得CD的长为 .
| 得分 | 评卷人 |
|
|
|
三、计算题（第17题每小题6分，第18题8分，共20分）
17．解下列方程：
（1）
（2）
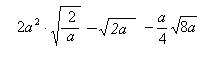18．已知a=8，求
3
的值
| 得分 | 评卷人 |
|
|
|
四、知识应用题（第19题8分,第20题8分,第21题10分,共26分）
19．2006年6月5日是中国第一个“文化遗产日”，铜陵市在铜都广场举办庆祝活动，我校承办了“责任与使命——亲近文化遗产，传承文明火炬”的活动，其中有一项“抖空竹”的表演．已知有塑料、木质两种质地的空竹，甲、乙、丙三名学生各自随机选用其中的一种空竹．求甲、乙、丙三名学生恰好选择同一种空竹的概率．
 | |||
 | |||
20．将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形．
(1) 要使这两个正方形的面积之和等于17cm2，那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗?若能，求出两段铁丝的长度；若不能，请说明理由。
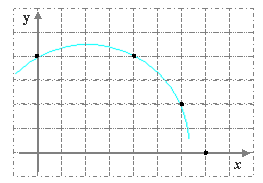
21．如图，已知直角坐标系中一条圆弧经过正方形网格的格点
A（0，4）、B（4，4）、C（6，2）
1) 用直尺画出该圆弧所在圆的圆心M的位置，并标出M点的坐标；
2) 若D点的坐标为（7，0），验证点D是否在经过点A、B、C的抛物线上；
3) 若D点的坐标为（7，0），想一想直线CD与⊙M有怎样的位置关系，并证明你的猜想。
 |
五、阅读理解（6分）
| 得分 | 评卷人 |
|
|
|
22.当抛物线的解析式中含有字母系数时，随着系数中字母取值的不同，抛物线的顶点坐标也将发生变化.例如：由抛物线y=x2-2mx+m2+2m-1……（1）
得：y=(x-m)2+2m-1……（2）
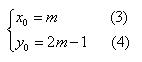∴抛物线的顶点坐标为(m，2m-1)，设顶点为P（x0，y0），则：
当m的值变化时，顶点横、纵坐标x0，y0的值也随之变化，将(3)代入(4)
得：y0=2x0-1. …(5)
可见，不论m取任何实数时，抛物线的顶点坐标都满足y=2x-1.
根据阅读材料提供的方法，确定抛物线y=x2-2mx+2m2-4m+3的顶点纵坐标y与横坐标x之间的函数关系式.