九年级数学上第二次月考测试题
(考试时间：120分钟 总分：150分 2007年10月12日)
一、选择题(每题3分，共36分)
1．若ax2-5x+3=0是一元二次方程，则不等式3a+6>0的解集是( )
A．a>-2
B．a<-2 C．a>-2且a≠0 D．a>
2．用反证法证明“若a⊥c,b⊥c,则a∥b”，第一步应假设（ ）
Ａ．a∥b Ｂ．a与b垂直 Ｃ．a与b不一定平行 Ｄ．a与b相交
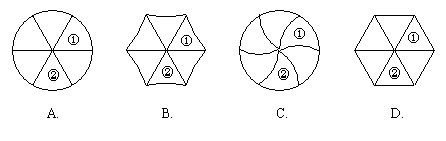
３．下列各图中，既可经过平移，又可经过旋转，由图形①得到图形②的是（ ）.
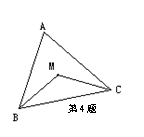
４．Ｍ是△ABC的内心，∠BMC=130°，则∠A的度数为
（ ）
Ａ．60° Ｂ．65° Ｃ．70° Ｄ．80°
５．若关于y的一元二次方程ky2－4y－3=3y＋4有实根，则k的取值范围是（ ）
A．k＞－
B．k≥－ 且k≠0
C．k≤－
D．k＞－
且k≠0
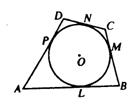
６．如图，四边形ABCD的边AB、BC、CD、DA和⊙O分别相
切于点L、M、N、P。若四边形ABCD的周长为20，则
等于（ ）
A. 5 B. 8 C. 10 D. 12
7．下列五个命题：（1）相等的圆心角所对的弧相等；（2）平分弦的直径垂直于弦；（3）任意一个圆有且只有一个内接三角形；（4）三角形的外心到各顶点距离相等。其中真命题有（ ）
A．1个 B．2个 C．3个 D．4个
8．⊙O的半径为3cm，点M是⊙O外一点，OM=4 cm，则以M为圆心且与⊙O相切的圆的半径一定是（ ）
A．1 cm或7 cm B．1 cm C．7 cm D．无法确定
9．在半径为R的圆中,内接正方形与内接正六边形的边长之比为（ ）
A．
׃1. B．2׃
. C．1׃. D．2׃3.
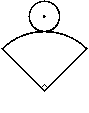10．如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型．若圆的半径为r，扇形的半径为R，扇形的圆心角等于90°，则r与R之间的关系是（ ）
A、R＝2r； B、
； C、R＝3r； D、R＝4r．
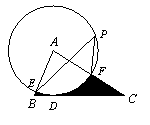11．如图，在△ABC中，，BC=4，以点A为圆心，2为半
径的⊙A与BC相切于点D，交AB于E，交AC于F，点P是
⊙A上一点，且∠EPF=40°，则图中阴影部分的面积是（ ）
A．
B．
C．
D．
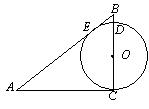12．如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，以BC上一点O为圆心作⊙O与AB相切于E，与AC相切于C，又⊙O与BC的另一交点为D，则线段BD的长为（ ）
A．1 B． 
C．
D． 
二、填空题(每题3分，共18分)
13．若关于
的方程x2＋mx＋4=0有两个不相等的整数根，则m的值为 ．
（只要写出一个符合要求的m的值）．
14．点P(
)与点Q
关于原点对称，则
。
15．在Rt△ABC中，∠C=90°，斜边AB=
，两直角边a、b的长是方程x2－(m+1)x+m=0的两根,则m=
.
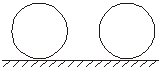
16．如下图，一枚直径为3的硬币沿着直线滚动一圈，圆心经过的距离是____ _. 。
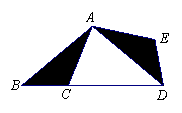
17．如上图所示，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转至在△ADE处，使点B落在BC的延长线上的D点处，则∠BDE= （度）．
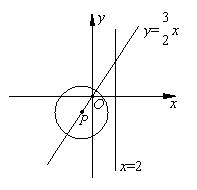
18．如图，P为正比例函数
图像上一个动点，⊙P的半径
为3，设点P的坐标为（x，y）．（1）当⊙P与直线x=2
相切时点P的坐标是 （2）当⊙P与直线x=2
相交时x的．取值范围是 ．
三、解答题(共96分)
19解方程：(每题5分，共10分)
(1) 
(2) x²-
x-
＝0
20．（6分）已知关于的方程
的两个实数根的平方和等于
，求实数
的值．
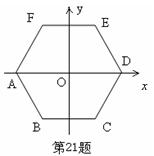21．（8分）如图，求中心点为原点，顶点A、D在x轴上，半径为2cm的正六边形ABCDEF的各个顶点的坐标。
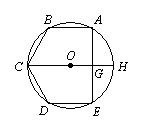
22．(6分)如图，⊙O上有A、B、C、D、E五点，且已知AB = BC = CD = DE，AB∥ED．
(1)求∠A、∠E的度数；
(2)连CO交AE于G。交于H，写出四条与直径CH有关的正确结论．(不必证明)
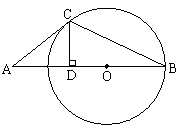23、（8分）如图，B、C是⊙O上的点，线段AB经过圆心O，连结AC、BC，过点C作CD
AB于D，
ACD=2B，AC是⊙O的切线吗？请说明理由？
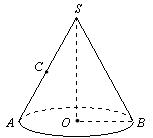
24．（10分）如图，有一座山，大致呈圆锥形，山脚呈圆形，半径4千米，山高
千米．在山坡SA的中点C有一联络站，要从山脚A修一盘山路，绕山坡一周将物资运往SA的中点C，这条公路的最短路程为多少?
 |
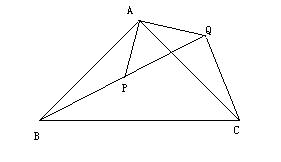
25、（12分）如图，⊿ABC中,BA=CA=4,∠BAC=90°,P是⊿ABC内一点，将⊿ABP绕点A逆时针旋转一定角度后能与⊿ACQ重合，且点B、P、Q在同一直线上，如果
∠BAP=30°，求AP的长。
26．（12分）如图①，AB是⊙O的直径，AC是弦，直线EF和⊙O相切于点C，AD⊥EF，垂足为D． （1）求证：∠DAC=∠BAC；
（2）若把直线EF向上平行移动，如图②，EF交⊙O于G、C两点，若题中的其它条件不变，这时与∠DAC相等的角是哪一个？为什么？
 |
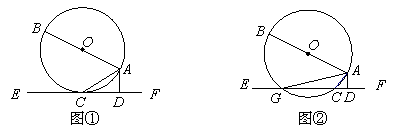27．（12分）在等腰三角形ABC中，∠A、∠B、∠C的对边分别为a、b、c，已知a＝３，b和c是关于的方程
的两个实数根．
(1)求△ABC的周长．
（2)求△ABC的三边均为整数时的外接圆半径．
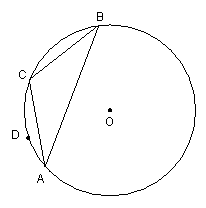
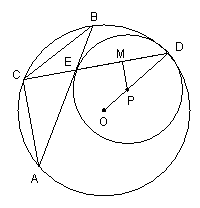
28．（本题满分12分）已知等腰△ABC,AC=BC,D是△ABC外接圆⊙O上的一点,直线CD与直线AB相交于点E,线段DE的中垂线与直线OD相交于P,以P为圆心,PD长为半径作⊙P.
(1)当点D在优弧AB上运动时(如左图),点D不与点A,B重合,⊙P与直线AB存在怎样的位置关系?请写出你的结论,并说明理由;
(2)当点D在劣弧AB上运动时(如右图),点D不与点A,B,C重合,(1)中的结论是否仍然成立.画出图形,并作出判断,说明理由;
 | |||
 | |||