锐角三角函数

九年级（下）第28章  锐角三角函数 单元测试2007-12

　　　　　　　　　　　　　　　　　　　　 姓名　　　　　　　  得分　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

一、选择题：（本大题共32分，第1－8题每小题3分，第9、10题每小题4分）

1在直角三角形中，各边的长度都扩大3倍，则锐角A的三角函数值　（　　）

A 也扩大3倍　B 缩小为原来的　 C　都不变　　　D 有的扩大，有的缩小、

2、sin²＋sin²(90°－) (0°＜＜90°）等于　　　　　　　　  （　　）

A　0　　　  B  1　　　  C　2　　　　 D  2sin²

3、已知为锐角，sin=cos50⁰则等于　　　 　　　　　　　　  （　　）

A 20⁰　　　　B 30⁰　　　　C 40⁰　　　　D 50⁰

4、如图，在△ABC中，∠C=90°，AC=8cm，AB的垂直平分线MN交AC于D，

连结BD，若cos∠BDC=，则BC的长是　　　　　　  　　　　 （　　）

A、4cm　　　　　 B、6cm　　 C、8cm　　 　 D、10cm

5以直角坐标系的原点O为圆心，以1为半径作圆。若点P是该圆上第一象限内的一点，且OP与x轴正方向组成的角为，则点P的坐标为　　　　　　　　　　 （　　）

A (cos,1)　 B (1,sin)　　C (sin,cos)　 D (cos,sin)

　　6、若tan(+10°)=，则锐角的度数是　　　　　　　　　　　(　　 )

 A、20°　　　B、30°　 C、35°　D、50°　　　　　

　　　　　  　第4题　　　　　　　　　　　  第8题　　　　　　　

7、如果、β都是锐角，下面式子中正确的是　　　　　　　　 （　　）

A、sin(+β)=sin+sinβ　　　 　 B、cos(+β)=时，+β=60⁰

C、若≥β时，则cos≥cosβ　　 D、若cos>sinβ,则+β>90⁰

8、如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上，量得

CD=8米，BC=20米，CD与地面成30º角，且此时测得1米杆的影长为2米，

则电线杆的高度为　　　　　　　 　　　　　　　　　　　　　 (　　)

A．9米　　B．28米　　C．米　　D.米

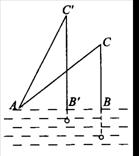
9、一次数学活动中，小迪利用自己制作的测角器测量小山的高度．已知她的眼睛与地面的距离为1.6米，小迪在处测量时，测角器中的（量角器零度线和铅垂线的夹角，如图）；然后她向小山走50米到达点处（点在同一直线上），这时测角器中的，那么小山的高度约为（　　）

Ａ．68米　　　　　　 Ｂ．70米　　　　　　 Ｃ．121米　　　　　　Ｄ．123米

（注：数据，供计算时选用）

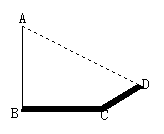
10、如图，钓鱼竿AC长6m，露在水面上的鱼线BC长m，某钓者想看看鱼钓上的情况，把鱼竿AC转动到的位置，此时露在水面上的鱼线为，则鱼竿转过的角度是　 　　　　　　 　　　　　　　　　　　　　　 ( 　 )

A．60°　　B．45°　　C．15°　　D．90°

二、填空题：（每小题3分，共24分）

11、已知tan＝，是锐角，则sin＝　　　

12、直角三角形ABC的面积为24cm²，直角边AB为6cm，∠A是锐角,则sinA＝　　　；

13、等腰三角形底边长10cm，周长为36cm，则一底角的正切值为　　　　　

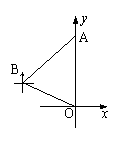
14、. 如图，机器人从A点，沿着西南方向，行了个4单位，到达B点后观察到原点O在它的南偏东60°的方向上，则原来A的坐标为　　　　.（结果保留根号）．

15、某人沿着坡度i=1:的山坡走了50米，则他离地面高　　　　米。

16、如图，在坡度为1：2 的山坡上种树，要求株距（相邻两树间的水平距离）是6米，斜坡上相邻两树间的坡面距离是　　　　 米。

17、在△ABC中，∠ACB＝90°，cosA=，AB＝8cm ，则△ABC的面积为______　

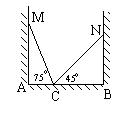
18、如图，在一个房间内有一个梯子斜靠在墙上，梯子顶端距地面的垂直距离MA为a米，此时，梯子的倾斜角为75°，如果梯子底端不动，顶端靠在对面墙上N，此时梯子的倾斜角45°，则这间房子的宽AB是　　　　  米。

三、解答题：（共94分）

19、计算(12分)：(1)tan30°sin60°＋cos²30°－sin²45°tan45°

(2)．

20、(12分)△ABC中，∠C＝90°

(1)已知：c＝ 8，∠A＝60°，　　　(2) 已知：a＝3， ∠A＝30°，

求∠B、a、b．　　　　　　　　  求∠B、b、c.

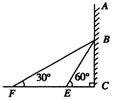
21、（8分）如图，在某建筑物AC上挂着一幅的宣传条幅BC，小明站在点F处，看条幅顶端B， 测得仰角为30°；再往条幅方向前行20m到达点E处，看条幅顶端B，测得仰角为60°，求宣传条幅BC的长．（小明的身高忽略不计，结果精确到0.1m）

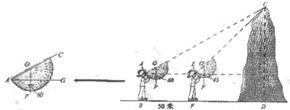
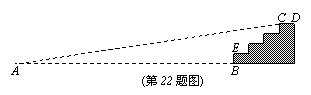
22、 (8分)如图山脚下有一棵树AB，小强从点B沿山坡向上走50m到达点D，用高为1.5m的测角仪CD测得树顶的仰角为10°,已知山坡的坡角为15°,求树AB的高.(精确到0.1m,已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)

　

　　

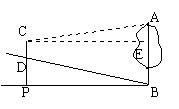
23、（8分）某商场门前的台阶截面如图所示．已知每级台阶的宽度(如CD)均为30cm，高度(如BE)均为20cm．为了方便残疾人行走，商场决定将其中一个门的门前台阶改造成供轮椅行走的斜坡，并且设计斜坡的倾斜角为9°．请计算从斜坡起点A到台阶前的点B的水平距离．(参考数据：sin9°≈0.16，cos9°≈0.99，tan9°≈0.16)

24、 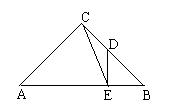(8分)如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连结CE,求sin∠ACE的值.

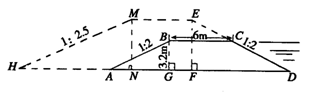
25、（8分）如图，拦水坝的横断面为梯形ABCD，坝顶宽BC为6m，坝高为3.2m，为了提高水坝的拦水能力，需要将水坝加高2m，并且保持坝顶宽度不变，迎水坡CD的坡度不变，但是背水坡的坡度由原来的i=1：2变成i′=1：2.5，（有关数据在图上已注明）．求加高后的坝底HD的长为多少？

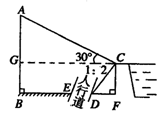
26、（10分）城市规划期间，欲拆除一电线杆AB，已知距电线杆AB水平距离14m的D处有一大坝，背水坡CD的坡度i=2：1，坝高CF为2m，在坝顶C处测得杆顶A的仰角为30°，D、E之间是宽为2m的人行道．试问：在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封上？请说明理由（在地面上，以点B为圆心，以AB长为半径的圆形区域为危险区域．）（≈1.732，≈1.414）

27、(10分) 已知Rt△ABC的斜边AB的长为10cm , sinA、sinB是方程

m(x²－2x)+5(x²+x)+12=0的两根。（1）求m的值；（2）求Rt△ABC的内切圆的面积。

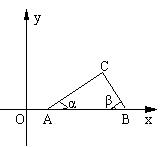
28、(10分)如图，点A(tanα，0)，B(tanβ，0)在x轴的正半轴上，点A在点B的左边，α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角；

　　(1)若二次函数y=－x²－kx+(2+2k－k²)的图象经过A、B两点，求它的解析式。

　　(2)点C在(1)中求出的二次函数的图象上吗?请说明理由。