苏科版九年级第一学期期中数学模拟试卷
一、选择题（本大题共12题，每题2分共24分，请把正确的选项涂在答题卡上）
1. 9的平方根是（ ）．
A、3 B、－3 C、±3 D、81
2. 
实数范围内有意义，则x的取值范围是（ ）
（A）x＞1 （B）x≥l （C）x＜1 （D）x≤1
3.如图，数轴上点
表示的数可能是（ ）B
A．
B．
C．
D．
4. 如图，在菱形ABCD中，不一定成立的（ ）
（A）四边形ABCD是平行四边形 （B）AC⊥BD
（C）△ABD是等边三角形 （D）∠CAB＝∠CAD
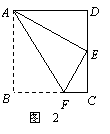5. 如图2，四边形ABCD为矩形纸片．把纸片ABCD折叠，使点B恰好落在CD边的中点E处，折痕为AF．若CD＝6，则AF等于 （ ）
（A）
（B）
（C）
（D）８
6. 在下列命题中，正确的是（ ）
A．一组对边平行的四边形是平行四边形 B．有一个角是直角的四边形是矩形
C．有一组邻边相等的平行四边形是菱形 D．对角线互相垂直平分的四边形是正方形
7. 已知关于x 的一元二次方程
有两个不相等的实数根，则m的取值范围是( ) A． m＞－1
B． m＜－2
C．m ≥0
D．m＜0
8. 某商品原价200元，连续两次降价a％后售价为148元，下列所列方程正确的是（ ）A：200(1+a%)2=148 B：200(1－a%)2=148
C：200(1－2a%)=148 D：200(1－a2%)=148
9.若关于z的一元二次方程
没有实数根，则实数m的取值范围是（ ） A．m<l B．m>-1 C．m>l D．m<-1
10. 用配方法解方程
，下列配方正确的是（ ）
A．
B．
C．
D．
11. 某种细胞开始有2个，1小时后分裂成4个并死去1个，2小时分裂成6个并死去1个，3小时后分裂成10个并死去1个，按此规律，5小时后细胞存活的个数是（ ）
A. 31 B. 33 C. 35 D. 37
12. 如图，是一次函数y=kx+b与反比例函数y=
的图像，则关于x的方程kx+b=的解为( )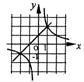
(A)xl=1，x2=2 (B)xl=-2，x2=-1 (C)xl=1，x2=-2 (D)xl=2，x2=-1
二、填空题（本大题共4题，每题3分，共12分）
13.在等边三角形、平行四边形、矩形、菱形、正方形、等腰梯形这些图形中，既是中心对称图形又是轴对称图形的有 个。
14. 已知矩形ABCD，分别以AD和CD为一边向矩形外作正三角形ADE和正三角形CDF，连接BE和BF，则
的值等于 。1
15. 写出一个两实数根符号相反的一元二次方程：__________________。
16. 图中标出了某校篮球队中5名队员的身高(单位：cm)，则他们的身高的方差是_________．
第二卷（非选择题部分，共95分）
三、解答题（本大题有4题，每题5分，共20分）
17. 
解：
18.解方程：x2＋3＝3(x＋1)．
解：
19.解方程：（用配方法） 
．
解：
20. .如图6，已知：ABCD中E是边AD的中点，BE的延长线与CD的延长线相交于点F.
求证：DE＝1/2BC (写出必要的推理依据)
证明：
四、选做题（（本大题共2小题，每小题有A、B两类题，A类题每题5分，B类题每题7分，你可以根据自己的学习情况，在每小题的两类题中任意选做一题，如果在同一小题中两类题都做，则以A类题计分）
21.（A类）已知x=2-
，求代数式x2-4x-6的值。
（B类）已知m是
的小数部分，求
的值。
解：我选做的是 类题
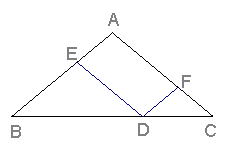
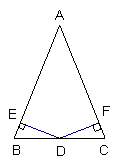22.（A类）已知：如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E、F，且DE＝DF。求证：△ABC是等腰三角形。
（B类）求证：等腰三角形底边的中点到两腰的距离相等。
解：我选做的是 类题
五、解答题（本大题共2题，每题7分，共14分）
23. 用直尺和圆规作一个菱形，使它的两条对角线分别等于已知线段a、b.
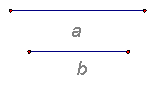如果a、b的长分别为6cm和8cm，请求出此菱形的面积.
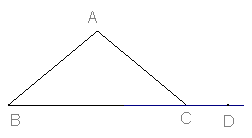
24.在等腰三角形ABC中，点D是直线BC上一点，DE∥AC交直线AB于E点， DF∥AB交直线AC于F点，请解答下列问题：
（1）如图，当点D在线段BC上时，证明：DE＋DF＝AB
（2）当点D在线段BC的延长线上时，请你参考（1）画出正确的图形，并写出线段DE，DF，AB之间的关系（不要证明）
六、解答题（本大题有2题，第25题7分，第26题8分，共15分）
25. 如图， 图是由边长为1的小菱形组成的网格，点A、B在网络格的格点上
（1）请你设计一种规则，用数字或符号表示点A的位置（画图并说明）
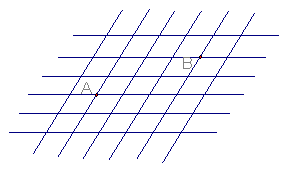（2）以同样的规则表示点B的位置。
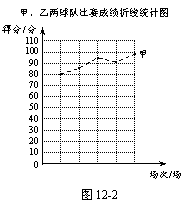
26.甲、乙两支篮球队在集训期内进行了五场比赛，将比赛成绩进行统计后，绘制成如图12-1、图12-2的统计图．
（1）在图12-2中画出折线表示乙队在集训期内这五场比赛成绩的变化情况；
（2）已知甲队五场比赛成绩的平均分
=90分，请你计算乙队五场比赛成绩的平均分
；
（3）就这五场比赛，分别计算两队成绩的极差；
（4）如果从甲、乙两队中选派一支球队参加篮球锦标赛，根据上述统计情况，试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析，你认为选派哪支球队参赛更能取得好成绩？
      | |||
      | |||
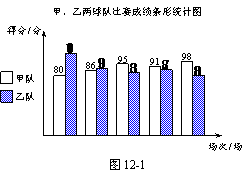七、解答题（本大题有2题，每小题8分，共16分）
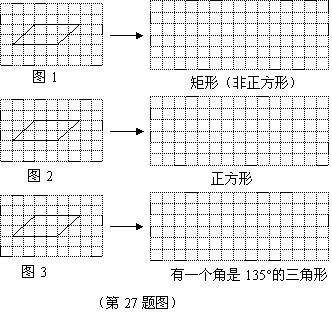
27. （07哈尔滨）现将三张形状、大小完全相同的平行四边形透明纸片，分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合（如图1、图2、图3）．
分别在图1、图2、图3中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，并把这两部分重新拼成符合下列要求的几何图形．
要求：
（1）在左边的平行四边形纸片中画一条裁剪线，然后在右边相对应的方格纸中，按实际大小画出所拼成的符合要求的几何图形；
（2）裁成的两部分在拼成几何图形时要互不重叠且不留空隙；
（3）所画出的几何图形的各顶点必须与小正方形的顶点重合．
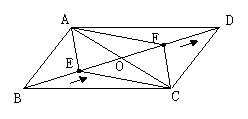
28. （10分）如图：□ABCD的对角线AC、BD相交于点O，BD=12cm，AC=6cm，点E在线段BO上从点B以1cm/s的速度运动，点F在线段OD上从点O以2cm/s的速度运动.
（1）若点E、F同时运动，设运动时间为t秒，当t为何值时，四边形AECF是平行四边形.
（2）在（1）的条件下，①当AB为何值时，四边形AECF是菱形；②四边形AECF可以是矩形吗？为什么？
