九年级数学第一学期学习效果自我评估(四)
数学试题卷
温馨提示:1、全卷满分为120分,考试时间120分钟.试卷共三大题,26小题.
2、请细心审题,严谨表达,相信你会有出色的表现.
参考公式:二次函数y=ax2+bx+c的图象的顶点坐标是![]() .
.
一、选择题(本题有lO小题。每小题3分,共30分。每小题只有一个选项是正确的。不选、多选、错选,均不给分。)
1.一个布袋中装有10个相同的球,其中9个红球,1个黄球,从中任意摸取一个,则( )
A.一定摸到红球 B.一定摸到黄球
C.不可能摸到黄球 D.很有可能摸到红球
2. 一个底面半径为
A. 80πcm2 B. 40πcm
 3.某一次函数的图像经过点(-1,2),且函数y的值随自变量x的增大而减小,则下列函数符合上述条件的是 ( )
3.某一次函数的图像经过点(-1,2),且函数y的值随自变量x的增大而减小,则下列函数符合上述条件的是 ( )
A. y=4x+6 B. y=-x C. y=-x+2 D. y=-3x-1
4.如图,已知点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是⊙O的五等分点,则
是⊙O的五等分点,则![]()
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
A.若x2=16,则x=4 B.若x2-xy-2y2=0(xy≠0),则![]() =2或
=2或![]() =-1.
=-1.
C.方程x(2x-1)=2x-1的解为x=1 .D.若分式![]() 值为零,则x=1或0
值为零,则x=1或0
6.下列关于相似的说法:①所有的等腰直角三角形一定相似;②所有的菱形一定相似;
③所有的全等三角形一定相似;④所有的位似图形一定相似;⑤所有的有个角为
 60°的等腰梯形一定相似. 其中说法正确的有 ( )
60°的等腰梯形一定相似. 其中说法正确的有 ( )
A. 5个 B. 4个 C. 3个 D. 2个
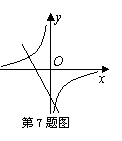
7.直线![]() 和双曲线
和双曲线![]() 在直角坐标系中的位置如图所示,下列结论:①k>0;②b>0;③k<0;④b<0. 其中正确的是( ) A.①② B.②③ C.③④ D.①④
在直角坐标系中的位置如图所示,下列结论:①k>0;②b>0;③k<0;④b<0. 其中正确的是( ) A.①② B.②③ C.③④ D.①④
8. 已知二次函数![]() 的图像经过(3,0)和(9,0), 则
的图像经过(3,0)和(9,0), 则
下面的判断中,错误的是( )
A.抛物线的对称轴是直线x=6; B.给出的条件不能确定顶点的坐标;
C.给出的条件不能确定抛物线开口向上还是向下; D.抛物线的顶点在第三象限
9. 如图,用一块直径为![]() 的圆桌布平铺在对角线长为
的圆桌布平铺在对角线长为![]() 的正方形桌面上,若四周下垂的最大长
的正方形桌面上,若四周下垂的最大长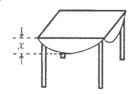 度相等,则桌布下垂的最大长度
度相等,则桌布下垂的最大长度![]() 为( )
为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
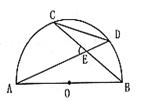 10. 如图,已知AB、CD分别是半圆O的直径和弦,AD和BC相交于点E,若∠AEC=α,则
10. 如图,已知AB、CD分别是半圆O的直径和弦,AD和BC相交于点E,若∠AEC=α,则
S△CDE:S△ABE等于( )
A.sinα B.cosα C.sin2α D.cos2α
二、填空题(本题有8小题,每小题3分,共24分)
11. x=1是方程x2-mx+6=0的一个根,则![]() = .
= .
12.在某一电路中,电源电压U保持不变为220V,电流I (单位:A)与电阻R
(单位:Ω)成反比例关系,则当电路中的电流I为
13.在△ABC中,∠C=90°,若∠B=2∠A,则tanB的值为 .
14.已知圆的面积为81πcm2,其圆周上一段弧长为3πcm,那么这段弧所对圆心角的度数是_________.
15.甲、乙两人上网都想进入A、B、C三个论坛中的一个(进入A、B、C中的哪一个可能性相同),则两人进入同一个论坛的概率是_______.
16.如图,将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若
AB:BC=4:5,则![]() 的值是_______.
的值是_______.
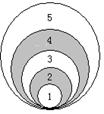
17. 如图, 同学们在操场的一个圆形区域内玩投掷沙包的游戏, 圆形区域由5个过同一点且半径不同的圆组成. 经过多次实验, 发现沙包如果都能落在区域内时, 落在2, 4两个阴影内的概率分别是0.36和0.21, 设最大的圆的直径是
 18.如图,动点P在函数
18.如图,动点P在函数![]() 的图像上运动,PM⊥
的图像上运动,PM⊥![]() 轴于M,PN⊥
轴于M,PN⊥![]() 轴于N,线段PM、PN分别与直线AB:
轴于N,线段PM、PN分别与直线AB: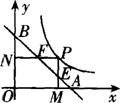
![]() 交于点E、F,则AF•BE的值是________.
交于点E、F,则AF•BE的值是________.

(第16题图) (第17题图) (第18题图)
三、解答题(本题有8小题,共66分)
19.(本题6分)给出三个多项式:![]() ,
,![]() ,
,![]() ,请你选择其中两个进行加法运算,并把结果因式分解.
,请你选择其中两个进行加法运算,并把结果因式分解.
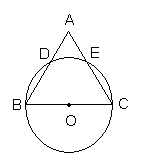
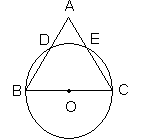 20. (本题6分) 如图,在△ABC中,以BC为直径的⊙O交AB于D,交AC于E,BD=CE. 求证:△ABC是等腰三角形.
20. (本题6分) 如图,在△ABC中,以BC为直径的⊙O交AB于D,交AC于E,BD=CE. 求证:△ABC是等腰三角形.
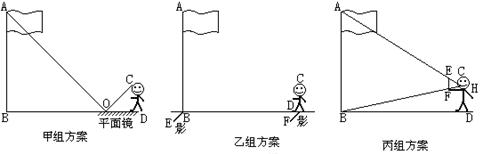 21. (本题8分)九年级某班的一节数学活动课上安排了测量操场上悬挂国旗的旗杆的高度.甲、乙、丙三个学习小组设计的测量方案如图所示:甲组测得图中BO=
21. (本题8分)九年级某班的一节数学活动课上安排了测量操场上悬挂国旗的旗杆的高度.甲、乙、丙三个学习小组设计的测量方案如图所示:甲组测得图中BO=
22.(本题8分) 有两个可以自由转动的均匀转盘A、B,都被分成了3等份,并在每份内均标有数字,如图所示,规则如下:①分别转动转盘A、B; ②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).
(1)用列表法(或树状图)分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
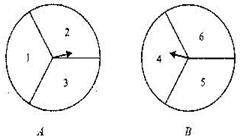 (2)小聪和小明想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小聪得2分;数字之积为5的倍数时,小明得3分. 这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏双方公平.
(2)小聪和小明想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小聪得2分;数字之积为5的倍数时,小明得3分. 这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏双方公平.
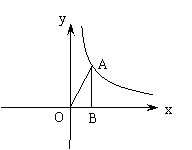
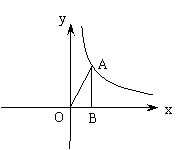 23.(本题8分)如图,第一象限内的点A在某反比例函数的图象上,过A作 AB⊥x轴,垂足为B,连结AO,已知△AOB的面积为4.
23.(本题8分)如图,第一象限内的点A在某反比例函数的图象上,过A作 AB⊥x轴,垂足为B,连结AO,已知△AOB的面积为4.
(1)求这个反比例函数的解析式;
(2)若点A的纵坐标为4,过点A的直线与x轴交于点P,且以A、P、B为顶点的三角形与△AOB相似,求所有符合条件的点P的坐标.
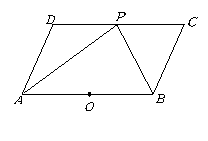
24.(本题10分)如图,在□ABCD中,![]() 是
是![]() 边上的一点,
边上的一点,![]() 与
与![]() 分别平分
分别平分![]() 和
和![]() .
.
(1)判断![]() 是什么三角形,证明你的结论;
是什么三角形,证明你的结论;
(2)比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
 (3)画出以
(3)画出以![]() 为直径的⊙O,交
为直径的⊙O,交![]() 于点
于点![]() ,连结
,连结![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,求证:
,求证: ![]() ,并求
,并求![]() 的值.
的值.
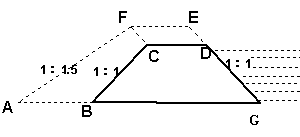
25.(本题10分)有一长
(1)求大坝横截面面积增加多少?
(2)已知这项工程由甲队单独做需40天完成;如果由乙队先单独做10天,那么剩下的工程还需要两队合做20天才能完成. 求乙队单独完成这项工程每天完成的土方数.
 |
26.(本题10分)已知:抛物线y=ax2+4ax+t与x轴的一个交点为A(-1,0).
(1)求抛物线与x轴的另一个交点B的坐标;
(2)D是抛物线与y轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式;
(3)E是第二象限内到x轴、y轴的距离的比为5:2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点P,使△APE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
2007学年第一学期九年级学习效果自我评估(四)
数学答题卷
一、选择题(本题有lO小题。每小题3分,共30分。每小题只有一个选项是正确的。不选、多选、错选,均不给分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(本题有8小题,每小题3分,共24分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 |
三、解答题(本题有8小题,共66分)
19.(本题6分)
解:
20.(本题6分)
 证明:
证明:
21. (本题8分)

解:你选择的方案是_________
22. (本题8分)
解:(1)
(2)
23. (本题8分)
 解:(1)
解:(1)
(2)
 24.(本题10分)
24.(本题10分)
解:(1)
(2)
(3)
 25. (本题10分)
25. (本题10分)
解:(1)
(2)
26. (本题10分)
解:(1)
(2)
(3)
2007学年第一学期九年级学习效果自我评估(四)
数学参考答案
一、选择题(本题有lO小题。每小题3分,共30分。每小题只有一个选项是正确的。不选、多选、错选,均不给分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | D | C | B | C | C | D | A | D |
二、填空题(本题有8小题,每小题3分,共24分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 |
| 5 |
| 600 |
|
| 8.44 | 1 |
三、解答题(本题有8小题,共66分)
19.(本题6分)
解:(![]() )+(
)+(![]() )=
)=![]()
(![]() )+(
)+(![]() )=
)=![]()
(![]() )+(
)+(![]() )
)![]()
 20. (本题6分)
20. (本题6分)
证明:![]()
![]()
![]()
![]()
![]()
21. (本题8分)
解:选择甲组方案计算:
在△ABO和△CDO中,因为∠ABO=∠CDO=90°,∠COD=∠AOB, 所以△ABO∽△CDO.
所以![]() ,所以
,所以![]() ,
,
又BO=![]() 即该校的旗杆为
即该校的旗杆为
连AE,CF,在△ABE和△CDF中,因为∠ABE=∠CDF=90°,∠AEB=∠CFD,
所以△ABE∽△CDF.所以![]() ,又CD=
,又CD=
所以![]() ,即该校的旗杆为
,即该校的旗杆为
选择丙组方案计算:
由FH∥BD,可得∠CFH=∠CBD,∠FCH=∠BCD,所以△CFH∽△CBD,![]() ,
,
又EF∥AB,可得∠FEC=∠BAC,∠FCE=∠BCA,△CFE∽△CBA,![]() ,所以
,所以![]()
又BD=![]() ,即该校的旗杆为
,即该校的旗杆为
22. (本题8分)
解:(1)每次游戏可能出现的所有结果列表如下:
| 转盘B的数字 转盘A的数字 | 4 | 5 | 6 |
| 1 | (1,4) | (1,5) | (1,6) |
| 2 | (2,4) | (2,5) | (2,6) |
| 3 | (3,4) | (3,5) | (3,6) |
表格中共有9种等可能的结果,则
数字之积为3的倍数的有五种,其概率为![]() ;
;
数字之积为5的倍数的有三种,其概率为![]() 。…………………………(4分)
。…………………………(4分)
(2)这个游戏对双方不公平.
∵小聪平均每次得分为![]() (分), 小明平均每次得分为
(分), 小明平均每次得分为![]() (分)
(分)
∵![]() ,∴游戏对双方不公平。
,∴游戏对双方不公平。
修改得分规定为:若数字之积为3的倍数时,小聪得3分;若数字之积为5的倍数时,小明得5分即可………………………(4分)
23. (本题8分)
解:(1)![]() ………………………(3分)
………………………(3分)
(2)A(2,4) B(2,0)
分两种情况:①当△APB∽△AOB时BP=BO=2 则P(4,0)
②当△APB∽△OAB时,AB2=OB·BP得BP=8 则P(10.0)或(-6,0)……………(5分)
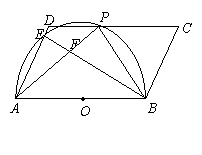 24. (本题10分)
24. (本题10分)
解:(1)![]()
![]()
又![]()
![]() ,
,![]() 分别平分
分别平分![]() ,
,![]()
![]()
![]() .
. ![]() 为直角三角形………………………(3分)
为直角三角形………………………(3分)
(2)![]()
![]()
![]()
![]()
![]()
同理证得![]()
![]() ………………………(3分)
………………………(3分)
(3)![]() ,
,![]()
![]()
![]() 是⊙O直径,
是⊙O直径,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ………………………(4分)
………………………(4分)
25. (本题10分)
(1)S梯形BGDC=45(m2) S梯形AGEF=69(m2)
∴大坝横截面面积增加69-45=24(m2)…………………………5分
(2)设乙独做需x天,则![]()
检验并解得:x=60 (24×90)÷60=36(土石方)
答略…………………………5分
26. (本题10分)
解:(1)依题意,抛物线的对称轴为y=x-2.
∵抛物线与x轴的一个交点为A(-1,0),
∴由抛物线的对称性,可得抛物线与x轴的另一个交点B的坐标为(-3,0).
…………………………3分
(2)∵抛物线y=ax2+4ax+t与x轴的一个交点为A(-1,0),
∴a(-1)2+
∵梯形ABCD中,AB∥CD,且点C在抛物线y=ax2+4ax+
∴C(-4,
∵梯形ABCD的面积为9,∴![]() (AB+CD)·OD=9.
(AB+CD)·OD=9.
∴![]() (2+4)│
(2+4)│
∴所求抛物线的解析式为y=x2+4x+3或y=-x2-4x-3.…………………………3分
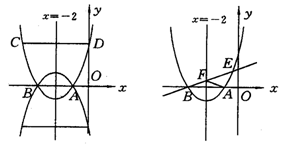 (3)设点E坐标为(x0,y0),依题意x0<0,y0>0,且
(3)设点E坐标为(x0,y0),依题意x0<0,y0>0,且![]() =
=![]() .∴y=-
.∴y=-![]() .
.
①设点E在抛物线y=x2+4x+3上, ∴y0=x02+4x0+3.
解方程组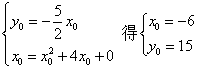 ∴
∴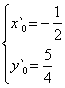
∵点E与点A在对称轴x=-2的同侧,∴点E坐标为(-![]() ,
,![]() ),
),
设在抛物线的对称轴x=-2上存在一点P,使△APE的周长最小.
∵AE长为定值,∴要使△APE的周长最小,只须PA+PE最小.
∵点A关于对称轴x=-2的对称点是B(-3,0),
∴几何知识可知,P是直线BE与对称轴x=-2的交点.
设过点E、B的直线的解析式为y=mx+n,∴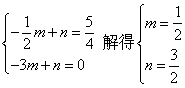
∴直线BE的解析式为y=![]() x+
x+![]() ,把x=-2代入上式,得y=
,把x=-2代入上式,得y=![]() ,
,
∴点P坐标为(-2,-![]() ).
).
②设点E在抛物线y=-x2-4x-3上,
∴y0=-x02-4x0-3.解方程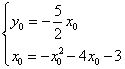 消去y0,得x02+
消去y0,得x02+![]() x0+3=0,
x0+3=0,
∴△<0,∴此方程无实数根.
综上.在抛物线的对称轴上存在点P(-2,![]() ),使△APE的周长最小.…………… 4分
),使△APE的周长最小.…………… 4分